2. Нормальное распределение случайной величины

Нормальное распределение случайной величины (распределение Лапласа–Гаусса) – это наиболее важное распределение в статистике. В обеспечении качества оно также играет центральную роль. Его широкое применение объясняется тем, что многие случайные величины достаточно близко описываются этим законом.

Особенность закона: он является предельным законом, к которому при определенных условиях приближаются другие законы. Нормальный закон проявляется в тех случаях, когда случайная переменная Х является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину Х влияет незначительно, и нельзя указать, какой именно влияет в большей степени, чем остальные.

Нормальное распределение (распределение Лапласа–Гаусса) – распределение вероятностей непрерывной случайной величины Х такое, что плотность распределения вероятностей при       <х<      принимает действительное значение:

ехр (3)

То есть, нормальное распределение характеризуется двумя параметрами  и , где  - математическое ожидание;  - стандартное отклонение нормального распределения.

Величина  ² – это дисперсия нормального распределения.

Математическое ожидание  характеризует положение центра распределения, а стандартное отклонение  (СКО) является характеристикой рассеивания (рис. 3).

f(x) f(x)

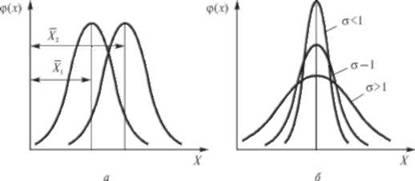
Рисунок 3 – Функции плотности нормального распределения с:

а) разными математическими ожиданиями ; б) разными СКО ^.

С ростом математического ожидания  обе функции сдвигается параллельно вправо. С убывающей дисперсией  ² плотность все больше концентрируется вокруг , в то время как функция распределения становится все более крутой.

Функция распределения (интегральная функция) имеет вид (рис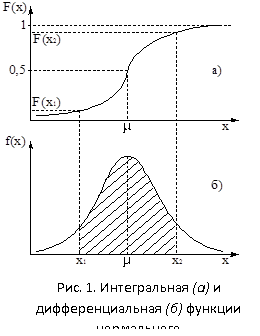. 4):

(4)

Рисунок 4 – Интегральная (а) и дифференциальная (б) функции нормального распределения

Особенно важно то линейное преобразование нормально распределенной случайной переменной Х, после которого получается случайная переменная Z с математическим ожиданием 0 и дисперсией 1. Такое преобразование называется нормированием:

(5)

Его можно провести для каждой случайной переменной. Нормирование позволяет все возможные варианты нормального распределения свести к одному случаю:  = 0,  = 1.

Нормальное распределение с  = 0,  = 1 называется нормированным нормальным распределением (стандартизованным).

Стандартное нормальное распределение (стандартное распределение Лапласа–Гаусса или нормированное нормальное распределение) – это распределение вероятностей стандартизованной нормальной случайной величины Z, плотность распределения которой равна:

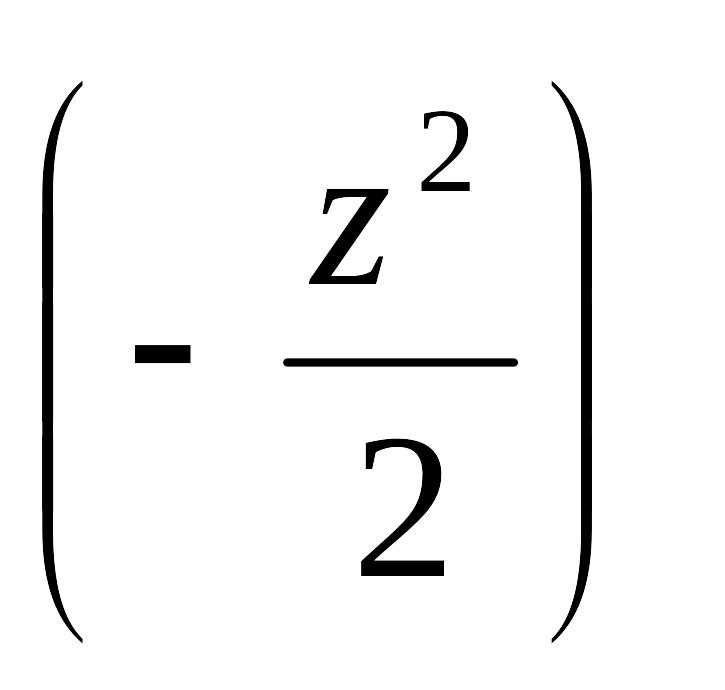
ехр (6)

при   <z<  

Значения функции Ф(z) определяется по формуле:

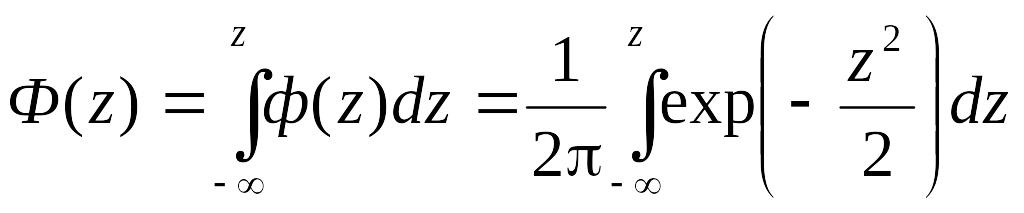  (7)

Значения функции Ф(z) и плотности ф(z) нормированного нормального распределения рассчитаны и сведены в таблицы (табулированы). Таблица составлена только для положительных значений z поэтому:

Ф (–z) = 1–Ф (z)    (8)

С помощью этих таблиц можно определить не только значения функции и плотности нормированного нормального распределения для заданного z, но и значения функции общего нормального распределения, так как:

;    (9)

.   (10)

Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины Х, подчиненной нормальному закону с параметрами  и , на определенный участок. Таким участком может быть, например, поле допуска на параметр от верхнего значения U до нижнего L.

Вероятность попадания в интервал от х₁ до х₂ можно определить по формуле:

(11)

Таким образом, вероятность попадания случайной величины (значение параметра) Х в поле допуска определяется формулой

(12)

Можно найти вероятность того, что случайная переменная Х окажется в пределах μ k.

Полученные значения для k =1,2 и 3 следующие (также смотрим рис. 5):

Границы	Число наблюдений между границами, %
μ–, μ+ μ–2, μ+2 μ–3, μ+3	68,26 95,44 99,73

Между 3σ-границами (μ-3σ; μ+3σ) находится 99,73% всех наблюдений, т. е. практически все значения. Только 0,27% значений находятся за этими границами, а именно 0,135% за границей μ+3σ и 0,135% – за μ-3σ .

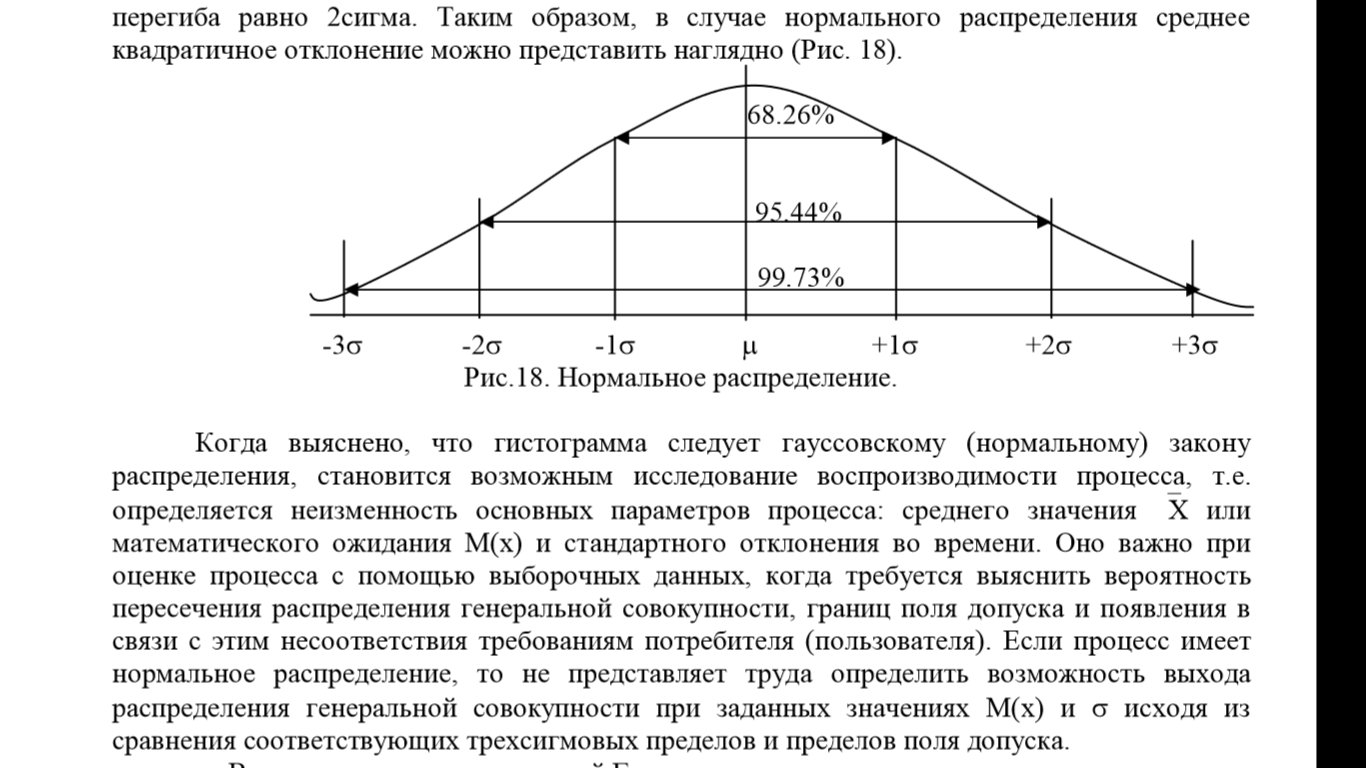
Рисунок 5 – Нормальный закон распределения.

Таким образом, если какое-либо значение появляется за пределами трехсигмового участка, в котором находятся 99,73% всех возможных значений, а вероятность появления такого события очень мала (1:270), следует считать, что рассматриваемое значение оказалось слишком маленьким или слишком большим не из-за случайного варьирования, а из-за существенной помехи в самом процессе, способной вызывать изменения в характере распределения.

Участок, лежащий внутри трехсигмовых границ, называют также областью статистического допуска соответствующей машины или процесса.