Вариант 30

1. Объектом моделирования является контейнер для перевозки зерна.

2. При моделировании контейнера ограничимся рассмотрением конструкций правильной пирамидальной формы и ценами на материалы, изготовление и транспортировку зерна, которые заданы по условию задачи.

3. Критерий оптимизации – величина полных затрат на материалы, изготовление контейнера и транспортировку зерна с его помощью: C, у.е.:

,

где C_м ‑ затраты на материалы, у.е.;

C_изг ‑ затраты на изготовление контейнера, у.е.;

C_тр ‑ затраты на транспортировку зерна, у.е.

4. Контейнер перед каждым рейсом будет наполняться зерном на его полный объём V_к, м³ и в результате весь объём зерна V_з = 400 м³, подлежащий транспортировке к переработчику, будет перевезен за N = V_з /V_к рейсов.

5. На критерий оптимизации влияют следующие факторы:

• цена материалов, необходимых для изготовления разных частей контейнера: днища P_дн = 30 у.е/м², боковых стенок P_бок = 20 у.е/м², крышки P_кр = 15 у.е/м²;

• цена 1 м резки и сварки при изготовлении контейнера P_изг = 25 у.е/м;

• цена одного рейса при транспортировке зерна P_тр = 32 у.е.;

Ценовые факторы являются внешними по отношению к моделируемой системе, поэтому в границах моделируемой системы нет факторов, с помощью которых можно влиять на цены. На все параметры моделируемой системы можно влиять, варьируя геометрические факторы конструкции контейнера:

• сторона крышки контейнера, a, м;

• сторона днища контейнера, b, м;

• высота контейнера, h, м.

6. Уравнения взаимосвязи целевой функции, факторов и параметров оптимизируемой системы:

Затраты на материалы для изготовления контейнера зависят от площади элементов конструкции (днища S_дн, м²; боковых стенок S_бок, м²; крышки S_кр, м²) и цен на материалы:

.

Площади крышки, днища и боковой поверхности контейнера можно выразить через варьируемые геометрические факторы:

,

_,

.

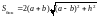Тогда затраты на материалы будут равны:

.

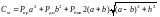Затраты на резку и сварку при изготовлении контейнера зависят от суммарной длины рёбер, которая составит:

,

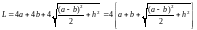а затраты на изготовление составят:

.

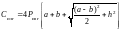Затраты на транспортировку зерна будут зависеть от количества рейсов:

.

Количество рейсов зависит от соотношения объёмов перевозимого зерна и объёма контейнера:

.

Объём контейнера найдём по формуле объёма правильной усечённой пирамиды:

.

Тогда затраты на транспортировку зерна составят:

.

Целевая функция равна сумме всех затрат:

7. Ограничения на факторы вытекают из условий транспортировки и их физической сущности:

,

,

.

8. Модель оптимизации в канонической форме:

Целевая функция:

Ограничения на факторы и параметры:

,

,

.

9. Математическая модель реализована в программе Mathcad.

10. Расчёты выполнены для двух ближайших к оптимальному решению целых значений количества рейсов. Результаты представлены в таблице:

    Факторы и параметры	Число рейсов
    	N = 24	N = 25
    Размеры контейнера, м:
    a	2,97	2,92
    b	1,97	1,95
    h	2,70	2,66
    Объём контейнера, V, м3	16,67	16,00
    Затраты, у.е:
    на материалы	790,43	769,29
    на изготовление	772,55	762,04
    на транспортировку	768,01	799,99
    полные	2330,99	2331,33

11. Анализ результатов показывает, что полные затраты для числа рейсов 24 и 25 практически одинаковы. Поэтому нет смысла делать дополнительный 25-й рейс, так как к сокращению затрат это не приводит, но увеличит время, затраченное на транспортировку. Следовательно, рекомендуем решение, соответствующее 24-м рейсам.