План решения задачи.

1. Внимательно прочитать условия задачи. Понять, что является объектом моделирования

2. Установить границы моделируемой системы.

3. Установить критерий оптимизации (целевую функцию).

4. Установить, какие параметры системы должны быть обеспечены.

5. Установить, какие факторы, влияют на критерий оптимизации.

6. Записать уравнения взаимосвязи целевой функции, факторов и параметров оптимизируемой системы.

7. Установить ограничения на параметры и факторы.

8. Записать математическую модель оптимизации в канонической форме.

9. Создать математическую модель в программе Mathcad.

10. Выполнить расчет оптимального варианта.

11. Выполнить анализ полученного решения.

12. Оформить результаты.

Решение задачи.

1. Объектом моделирования является контейнер для перевозки зерна.

2. При моделировании контейнера ограничимся рассмотрением конструкции контейнера в форме правильной четырёхгранной пирамиды.

3. Критерий оптимизации – величина полных затрат на изготовление контейнера и транспортировку зерна с его помощью: C, у.е. При этом полная величина затрат будет зависеть:

• от затрат на материалы, необходимые для изготовления контейнера C_м;

• от затраты на резку и сварку металла при изготовлении контейнера C_изг;

• от затрат на транспортировку всего объёма зерна C_тр.

То есть целевая функция будет представлена как:

.

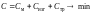4. Контейнер перед каждым рейсом будет наполняться зерном на его полный объём V_к, м³ и в результате весь объём зерна V_з = 400 м³, подлежащий транспортировке к переработчику, будет перевезен за N рейсов.

5. На критерий оптимизации влияют следующие факторы:

• цена материалов, необходимых для изготовления разных частей контейнера: днища P_дн = 30 у.е/м², боковых стенок P_бок = 20 у.е/м², крышки P_кр = 15 у.е/м²;

• цена 1 м резки и сварки при изготовлении контейнера P_изг = 25 у.е/м;

• цена одного рейса при транспортировке зерна P_тр = 32 у.е.;

Ценовые факторы являются внешними по отношению к моделируемой системе, поэтому в границах моделируемой системы нет факторов, с помощью которых можно влиять на цены. На все параметры моделируемой системы можно влиять, варьируя геометрические факторы конструкции контейнера:

• сторона крышки контейнера, a, м;

• сторона днища контейнера, b, м;

• высота контейнера, h, м.

6. Запишем уравнения взаимосвязи целевой функции, факторов и параметров оптимизируемой системы.

Затраты на материалы для изготовления контейнера зависят от площади отдельных элементов конструкции (днища S_дн, м²; боковых стенок S_бок, м²; крышки S_кр, м²) и соответствующей цены на материалы:

.

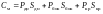Площади крышки, днища и боковой поверхности контейнера можно выразить через варьируемые геометрические факторы – длину, ширину и высоту контейнера:

,

_,

.

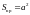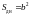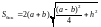Тогда затраты на материалы составят:

.

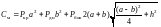Затраты на резку и сварку при изготовлении контейнера зависят от суммарной длины рёбер, которая равна:

,

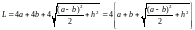а затраты на изготовление составят:

.

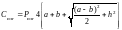Затраты на транспортировку зерна будут зависеть от количества рейсов:

.

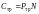Количество рейсов зависит от соотношения объёмов перевозимого зерна и объёма контейнера:

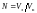
Объём контейнера найдём по формуле объёма правильной усечённой пирамиды:

.

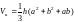Тогда затраты на транспортировку зерна составят:

.

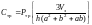7. На факторы необходимо установить ограничения, вытекающие из условий транспортировки (размеры контейнера не должны превышать 4 м) и физической сущности факторов (размеры не могут быть отрицательными числами):

,

,

.

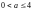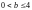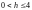8. Модель оптимизации в канонической форме имеет вид:

Целевая функция:

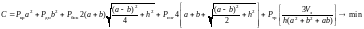
Ограничения на факторы и параметры:

,

,

.

9. Создадим математическую модель в программе Mathcad. Введем постоянные параметры:

Зададим целевую функцию, как функцию пользователя от варьируемых факторов:

В качестве стартовой точки выберем середину интервала варьирования факторов и вычислим значение целевой функции в этой точке:

Создадим блок решения оптимизационной задачи, задаваемый ключевым словом Given:

10. Выведем рассчитанные значения факторов и параметров модели в оптимальной точке:

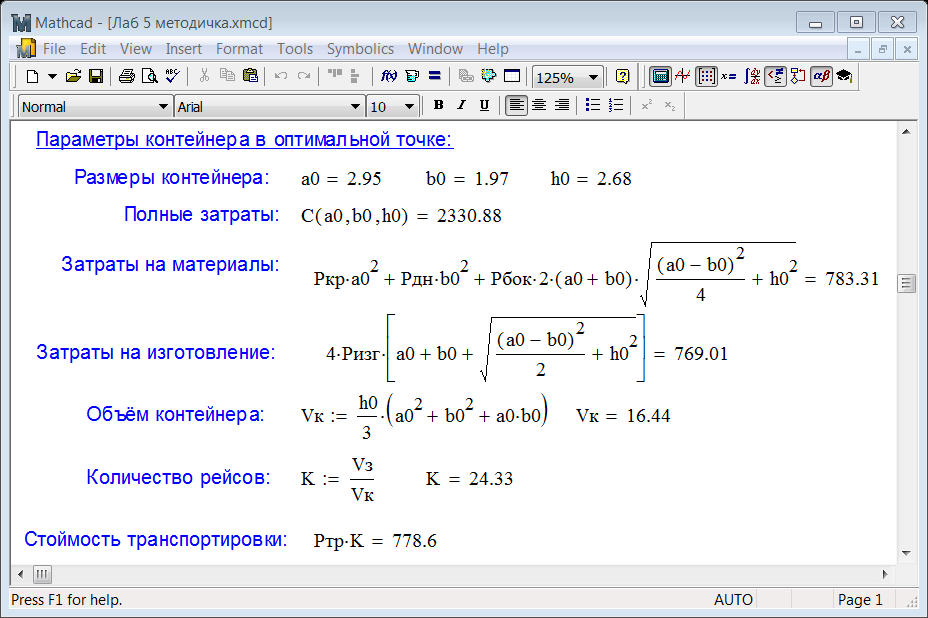
Анализ решения показывает, что количество рейсов, необходимых для транспортировки зерна, равно 24.5, то есть фактически 25, что означает – дополнительный 25-й рейс будет совершен с полупустым контейнером. Поэтому надо сравнить, что для нас экономически выгодно: сделать контейнер немного меньшего объема (более дешёвый) и 25 рейсов, либо контейнер чуть больше, но перевезти зерно за 24 рейса, сэкономив к тому же время на перевозку.

Для проведения такого анализа необходимо ввести в блок решения оптимизационной задачи дополнительное ограничение на выбранное число рейсов и выполнить оптимизацию дважды, задав в этом ограничении поочередно 24 и 25 рейсов.

Ограничение на число рейсов задается в виде тождества:

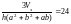или

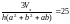
Для ввода данного выражения в Mathcad необходимо использовать знак «тождественно равно», находящийся на панели команд Boolen. В качестве стартовой точки выберем найденные оптимальные значения факторов:

Выведем результаты решения для числа рейсов 24:

Аналогично найдём решение для числа рейсов 25:

Для сравнения полученных результатов и выбора наиболее экономичного варианта сведём данные в таблицу:

Факторы и параметры	Число рейсов
	N = 24	N = 25
Размеры контейнера, м:
a	2,97	2,92
b	1,97	1,95
h	2,70	2,66
Объём контейнера, V, м3	16,67	16,00
Затраты, у.е:
на материалы	790,43	769,29
на изготовление	772,55	762,04
на транспортировку	768,01	799,99
полные	2330,99	2331,33

10. Анализ результатов показывает, что полные затраты для числа рейсов 24 и 25 практически одинаковы (разница составляет 0,34 у.е.). Будем считать, что если разница в стоимости 2-х вариантов не превышает 1 у.е., то она для нас не существенна. Поэтому нет смысла делать дополнительный 25-й рейс, так как к существенному сокращению затрат это не приведёт, но увеличит время, затраченное на транспортировку. Следовательно, рекомендуем решение, соответствующее 24-м рейсам.

11. Оформление результатов: