Утверждаю Заведующий кафедрой ОНИП докт. техн. наук, профессор

__________ Дашков В.Н.

«__» ______ 2013

Основы научных исследований и моделирование м5. Контрольное задание № 3

Оптимизация многофакторных технических систем

Составители:

М.М. Дечко, доцент кафедры «Основы научных исследований и проектирования» Учреждения образования «Белорусский государственный аграрный технический университет», кандидат технических наук

Лабораторная работа № 4

Оптимизация многофакторных технических систем

Цель работы: Освоить методы математического моделирования и оптимизации многофакторных технических систем.

Построение модели для решения задачи оптимизации включает следующие этапы:

1. Установить границы системы, подлежащей оптимизации.

2. Определить количественный параметр (критерий оптимизации), на основе которого можно произвести анализ вариантов для выявления наилучшего.

3. Выбрать внутрисистемные независимые переменные (факторы), которые используются для расчёта параметров системы и сравнения вариантов решений.

4. Построить математическую модель, отражающую взаимосвязь между факторами и параметрами системы.

5. Определить систему ограничений на допустимые значения факторов и параметров.

Критерий оптимизации: ― количественная оценка оптимизируемой характеристики системы, позволяющая выбрать наилучший вариант из множества возможных. Наилучшему варианту всегда соответствует минимальное или максимальное значение критерия оптимизации. Только один критерий может использоваться для определения оптимума.

Уравнение, описывающее зависимость критерия оптимизации от факторов моделируемой системы, называется ― целевая функция.

Необходимо определить основные независимые переменные, которые оказывают существенное влияние на функционирование системы. Количество выбранных переменных – компромисс, так как большое количество переменных усложняет решение задачи, малое количество может привести к неоптимальному решению.

М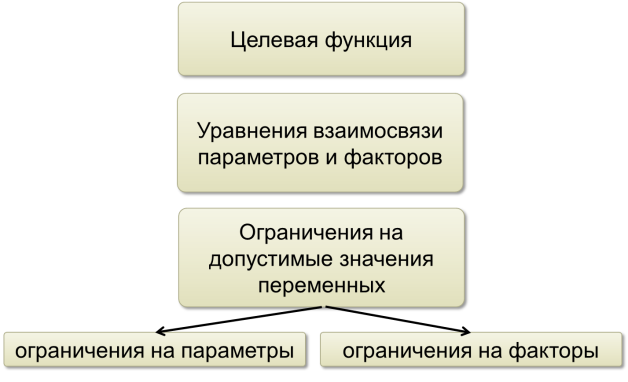 атематическая модель включает уравнения, описывающие физические процессы, протекающие в системе, уравнения материальных и энергетических балансов, а также соотношения, связанные с проектными решениями. Такие уравнения позволяют рассчитывать параметры системы, характеризующие ее функционирование. Эти уравнения обычно дополняются неравенствами, которые определяют область допустимых значений независимых переменных, накладывают ограничения на верхние и/или нижние границы изменения характеристик функционирования системы (параметров) или устанавливают лимиты имеющихся ресурсов. Таким образом, элементы математической модели содержат всю информацию, которая обычно используется при расчетах и оценках качества проекта или прогнозирования характеристик инженерной системы. Структура математической модели для решения оптимизационной задачи приведена на рисунке.

Для решения задачи оптимизации технической системы с помощью программы Mathcad необходимо выполнить следующие шаги:

1. Задать целевую функцию, как функцию пользователя от оптимизируемых факторов.

2. Задать стартовые значения оптимизируемых факторов, реализующие любое допустимое решение (решение, соблюдающее все ограничения на допустимые значения факторов и параметров).

3. Создать блок решения с помощью ключевого слова Given.

4. Задать ограничения на факторы и параметры.

5. Найти оптимальное решение с помощью функции Minimize() (при поиске минимума целевой функции) или Maximize() (при поиске максимума целевой функции).

Пример решения задачи (вариант 30).

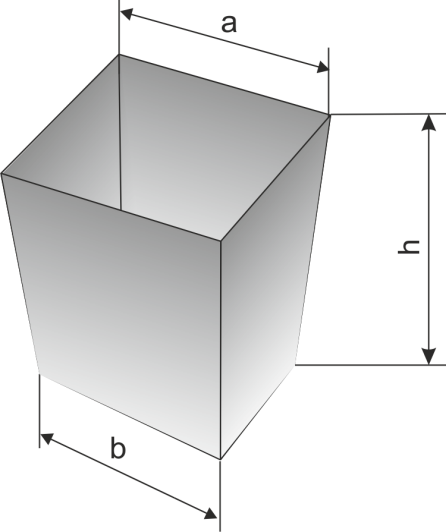
Формулировка задачи. Требуется перевезти из зернохранилища на переработку 400 м³ зерна. Для перевозки груза необходимо спроектировать и изготовить контейнер, показанный на рисунке. По условиям транспортировки размеры контейнера в каждом измерении не должны превосходить 4 м. Контейнер изготавливается из листовой стали с применением резки и сварки. Известны следующие данные:

• стоимость каждого рейса по транспортировке контейнера с зерном к переработчику и обратно к зернохранилищу равна 32 у.е.;

• стоимость материалов для изготовления днища контейнера – 30 у.е/м², боковых стенок контейнера – 20 у.е./м²; крышки контейнера – 15 у.е./м².

• с тоимость работ по резке и сварке материалов зависит от суммарной длины рёбер контейнера и на единицу длины равна 35 у.е./м.

Сконструируйте контейнер с такими размерами a b h, чтобы минимизировать полные затраты на изготовление контейнера и перевозку зерна.