7.4.4 Контактномеханический метод

Особенности метода. К особенностям метода относится протекание процесса при временном контакте электродов, что возможно только в случае использования низкого напряжения, когда сопротивление окисных пленок достаточно для предотвращения импульса тока. Окисные пленки на металлах являются полупроводниками, и между электродами протекает ток, который, ввиду малой толщины пленки, создает плотность выше предельной, т.е. обеспечивает анодный съем припуска в местах контакта электродов. При этом скорость удаления металла зависит от толщины пленки, изменяющейся под действием контактного давления, например, в зубчатых передачах. В этом случае достигается локальное удаление припуска на аноде и его выравнивание относительно теоретического профиля. Такой процесс используется при ремонте и восстановлении контактных пар (зубчатых колес, шлицевых соединений), когда одна из деталей сохраняет требуемую точность профиля (например, зубчатое колесо большого диаметра) или такая деталь заменена на новую, изготовленную с заданной точностью.

В случае износа профиля зубьев (шлицев) на обоих колесах и при наличии припуска на обработку за счет остаточной (после эксплуатации) части допуска на толщину зуба можно использовать переменную полярность, где обработка происходит по схеме притирки и может снизиться имеющееся нарушение теоретического профиля, например, эвольвенты.

Механизм протекания процесса. На примере зубчатых передач показано, что местные разрушения профиля при эксплуатации, как правило, вызывают концентрацию напряжений, несовместимую с дальнейшей эксплуатацией узлов, и такие зубчатые колеса необходимо заменять.

При расчете технологических режимов учитывают, что в любом случае износ одного из колес (как правило, меньшего диаметра) существенно выше, поэтому параметры процесса находят, принимая колесо с меньшим износом кондиционным (что в большинстве случаев отвечает реальности).

Тогда расчетная схема для управления процессом отвечает приведенной на рис. 7.12, где приняты следующие начальные условия: износ по профилю зуба имеет плавные переходы между участками; минимальный припуск имеет положительное значение относительно нижнего предельного контура зуба (граница 3 на рис. 7.12); металлический контакт между сопрягаемыми зубьями отсутствует, т.е. в точке «а» (рис. 7.12) имеется некоторый слой рабочей среды, препятствующий соприкосновению частей 1;2 при доводке.

Граничным условием будет

, (7.30)

где z_min – минимальный припуск относительно нижней границы допуска на толщину зуба для заданной степени точности зубчатой передачи.

Для выполнения граничного условия (7.30) необходимо рассчитать величину неравномерности припуска (Δz) в конце доводки.

Рис 7.12. Расчетная схема процесса при доводке профиля зуба:

1 - профиль не изношенного зуба; 2 - контур сечения изношенного зуба с рабочей стороны; 3 - нижняя граница по толщине изношенного зуба;

4 - вязкий приэлектродный слой; Zmax – предельный допуск на обработку изношенного зуба; Zmin – минимальный припуск на обработку изношенного зуба; z – неравномерность припуска по профилю.

Если принять, что в точке «а» (рис. 7.12) имеется пограничный слой с повышенной вязкостью, то его толщина, определяющая минимальный межэлектродный зазор при доводке, рассчитывается по зависимости [4]:

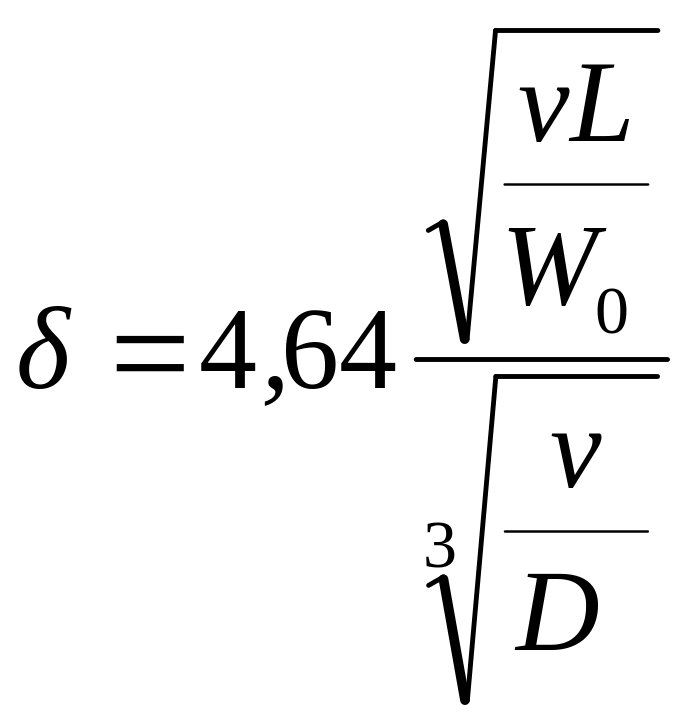, (7.31)

где ν - кинематическая вязкость среды;

L – длина зоны обработки;

W₀- средняя скорость перемещения рабочей среды;

D – коэффициент диффузии.

Для расчета D предлагается [4] эмпирическая зависимость

D=0,96 10^-3 1+0,0289 (Т-273).

Вязкость  в рабочей среде [10] в зоне точки «а» (рис. 6.21) имеет значение, соответствующее вязкости индустриального машинного масла при Т=315 К.

Длина зоны обработки может быть принята равной дуге перекрытия зубчатой передачи, которая составляет

L=p_i,

где  - коэффициент перекрытия. Величина «» выбирается в пределах 1,2-1,5;

p_i –шаг между зубьями по начальной окружности

p_i = ,

где m - модуль колеса.

Среднюю скорость перемещения рабочей среды W₀ можно найти при условии, что вязкая среда перемещается в зоне контакта зубьев с проскальзыванием. Тогда для дуги перекрытия L при частоте вращения n

W₀ = KLn= K p_in, (7.32)

где К – коэффициент проскальзывания, учитывающий отставание жидкости от зоны контакта колес; выбирается аналогично параметрам шестеренчатых насосов.

Из [4] известно, что нижний предел скорости течения рабочей среды для электрохимической размерной обработки составляет 0,5 м/с.

Тогда можно найти частоту вращения передачи

, (7.33)

где z_зуб – число зубьев колеса;

D_д – диаметр обрабатываемого колеса по делительной окружности.

Правомерно также предположение, что для оценочных расчетов неравномерности припуска в конце обработки профиля зуба, когда z_min0, величина z не должна превышать величины допуска на толщину зуба. Плотность тока (а следовательно и локальный съем припуска) на всех участках профиля изменяется обратно пропорционально изменению межэлектродных зазоров. По рис. 7.12 минимальный зазор в точке «а» составляет S₁, а максимальный (точка «б») –

S₂ = S₁ + z(),

где z() – изменение неравномерности припуска в течение времени обработки .

Тогда без учета перекрытия зубьев скорость съема материала (V) при доводке по [4], в точках «а» и «б» составит

. (7.34)

Время удаления припуска _б определяется через съем z_min (точка «б» на рис. 7.12) при условии достижения z  _n .

Из (7.58)

.

После преобразований

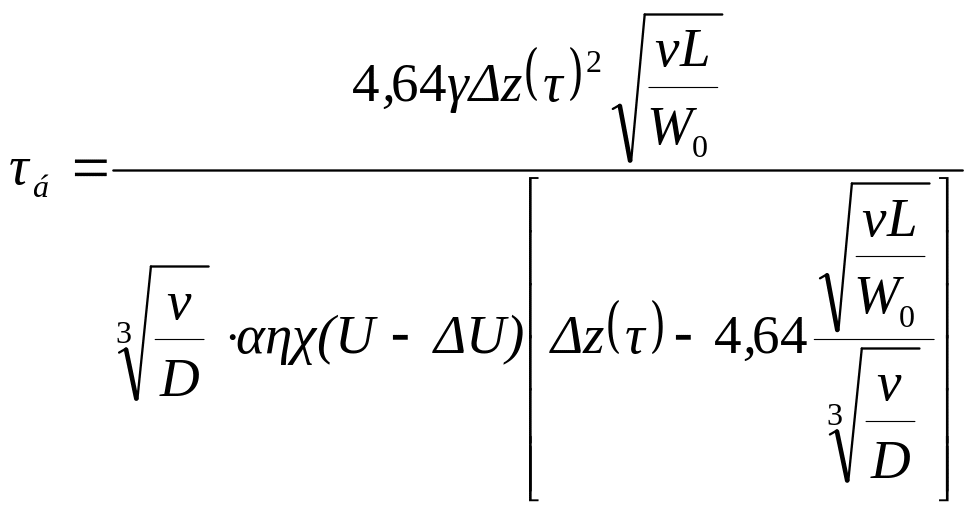. (7.35)

Очевидно, что время обработки участков в точках «а» и «б» одинаково (_а = _б = ), хотя скорость анодного растворения в точке «а» будет существенно выше, т.к. величина «» измеряется микронами и при выполнении условия массовыноса [4] повышенный съем материала в точке «а» будет снижать неравномерность припуска.

Для выполнения граничного условия необходимо в конце доводки получить (рис. 7.12)

z  0.

C учетом (7.59)

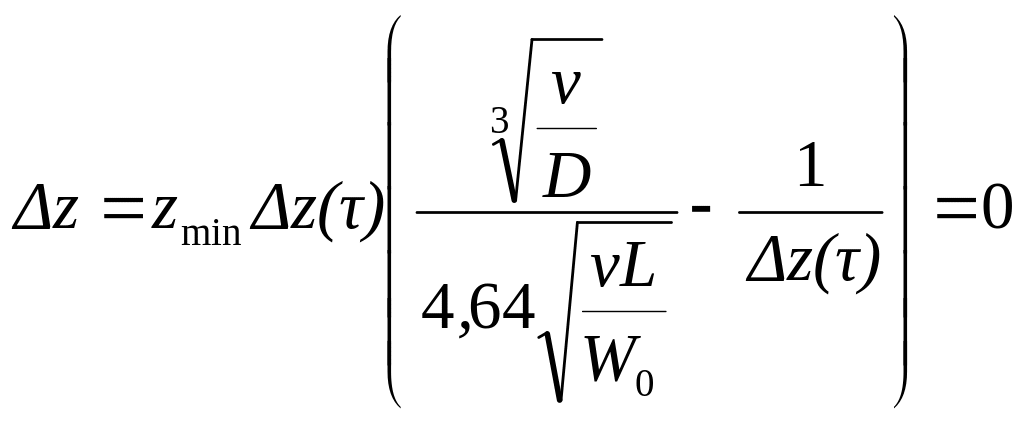, (7.36)

где L, W₀ – находят по (7.35).

Откуда находят z_min, определяющий пригодность колеса к ремонту.

Решение уравнения (7.35) позволяет также найти время обработки (), при котором выполняется условие (7.36). Учитывая малую величину z относительно общего припуска, решение может быть выполнено дискретным методом последовательных приближений.

Число проходов в процессе доводки можно найти, зная из зависимости (7.34), какое количество металла с поверхности удаляется за 1 оборот колеса (z'). Тогда отношение припуска на обработку к величине съема металла за проход даст искомую величину.

Число проходов при доводке должно быть кратным отношению z_min к предельной погрешности z' c округлением в сторону увеличения до целого числа (m_пер):

. (7.37)

Если m_пер=1, то расчет выполняется по (7.35). В других случаях находят суммарное время обработки ₀.

Съем z_min можно представить как дискретное удаление припуска z_{m min} при числе переходов m _пер.

, (7.38)

где

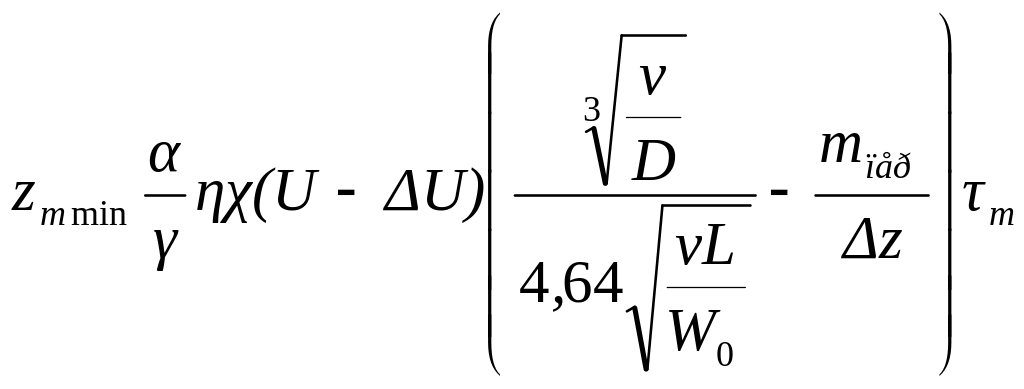. (7.39)

_m - общее время обработки одного зуба.

Управление дискретным процессом доводки с удалением припуска z_min возможно по времени обработки ₀

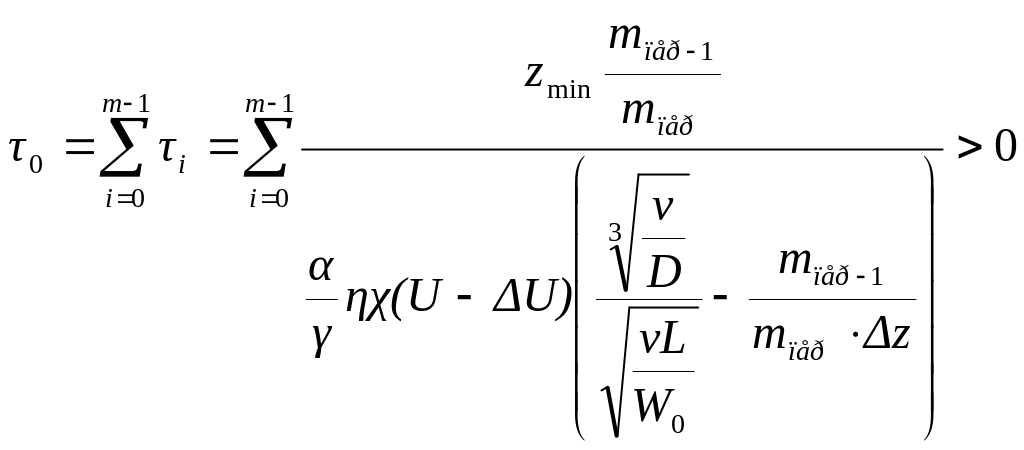. (7.40)

Если полученное время обработки превышает расчетное по зависимости (7.35), то его берут равным  по (7.35).

Если расчетное ₀0, то принимают ₀=0, что показывает возможность получения требуемого профиля при сохранении части припуска на обработку по контуру зуба без доводки.

Следует отметить, что величина ₀ определяет время обработки изношенной поверхности одного участка , а не всего колеса.

Общее время обработки определяется как

_общ = ₀, (7.41)

где Н – длина обрабатываемой поверхности, то есть поверхности, на которой происходит контакт зубьев;

– длина участка, на котором обработка идет в данный момент времени.

В работах по трибологии приводится частная зависимость для цилиндрических поверхностей, разделенных смазкой, где средний зазор «S» определяется по формуле

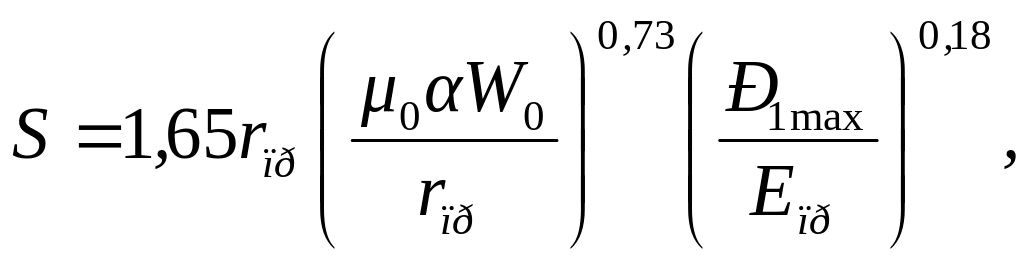(7.42)

где Р_{1 max} – максимальное давление среды в зоне контакта;

₀ – средняя динамическая вязкость среды в зазоре;

r_пр – приведенный радиус кривизны;

W₀ – скорость относительного перемещения поверхностей;

Е_пр – приведенный модуль упругости (выбирается из справочников);

 - пьезокоэффициент вязкости среды при температуре входа ее в зону контакта (выбирается из справочников).

Из (7.42) при средней вязкости среды ₀ можно найти силу давления в зоне контакта Р₁:

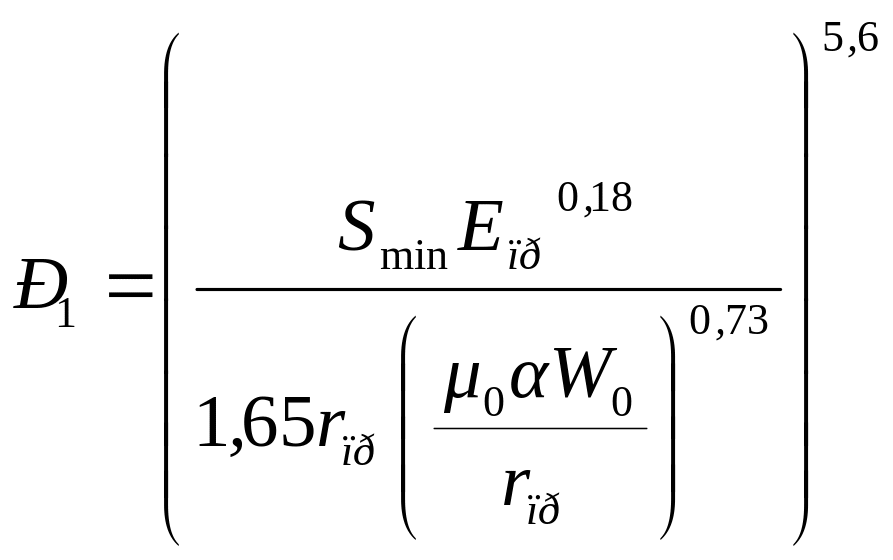(7.43)

С некоторым приближением величину S_min можно оценить по зависимости

S_min=K₁(Rz₁+Rz₂), (7.44)

где К₁ – коэффициент, учитывающий максимальные неровности профиля (К₁=1,2-1,5).

Имея геометрические размеры рычагов установки и колес определяют силу торможения, при которой следует выполнить доводку колеса.

372