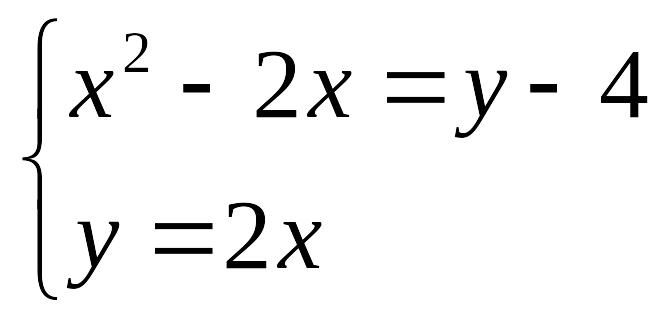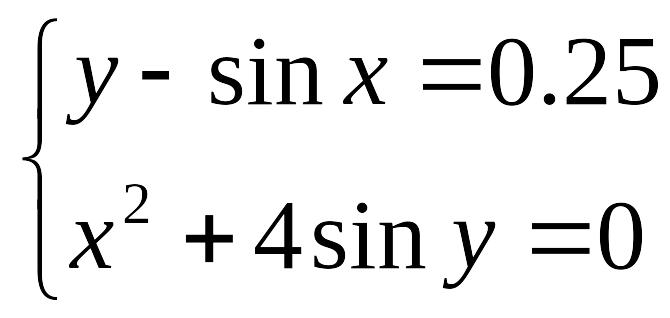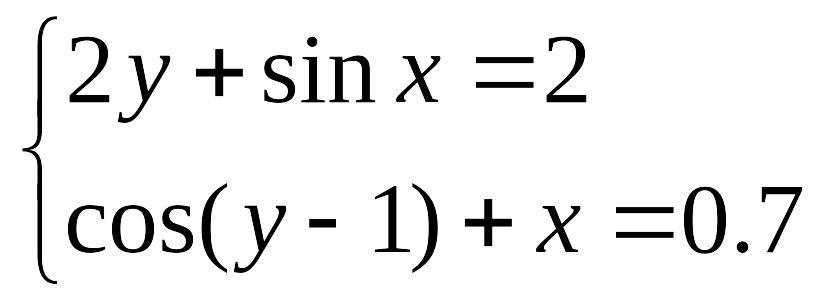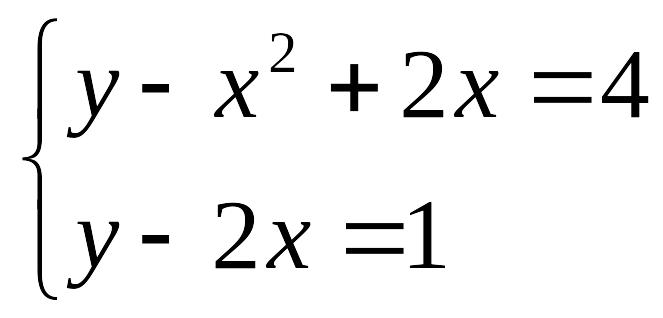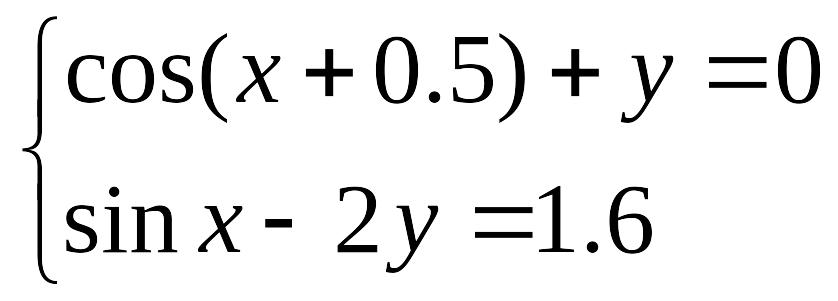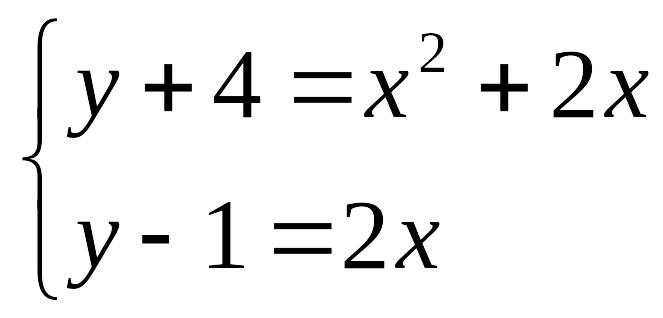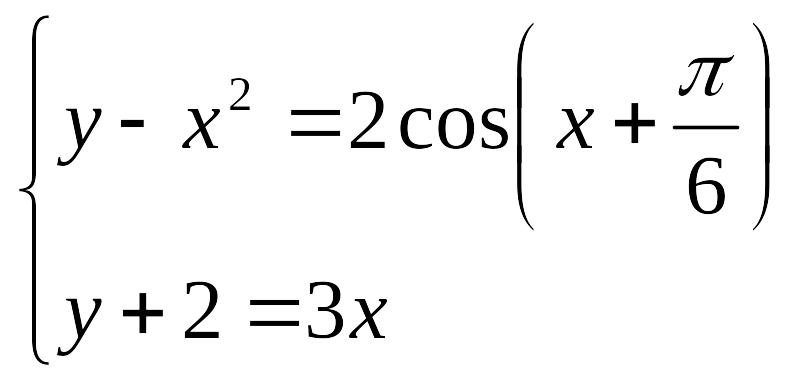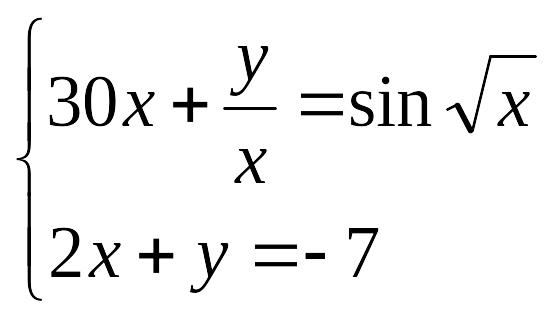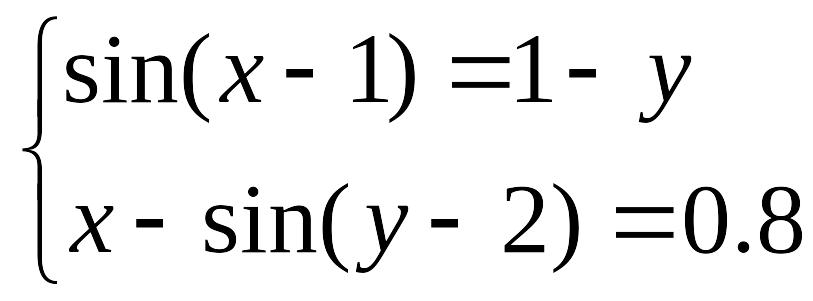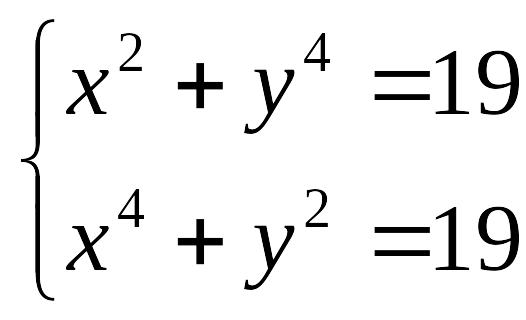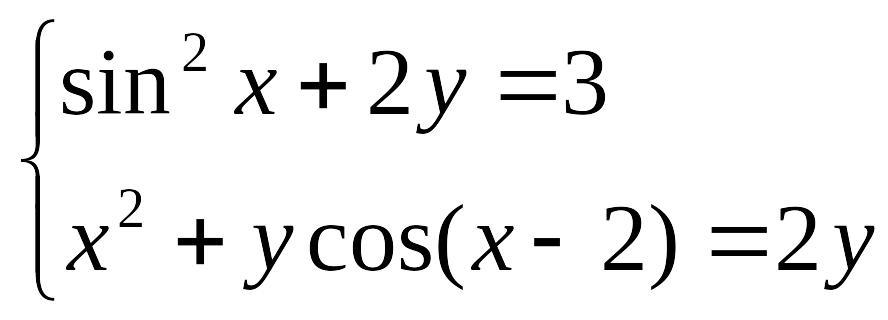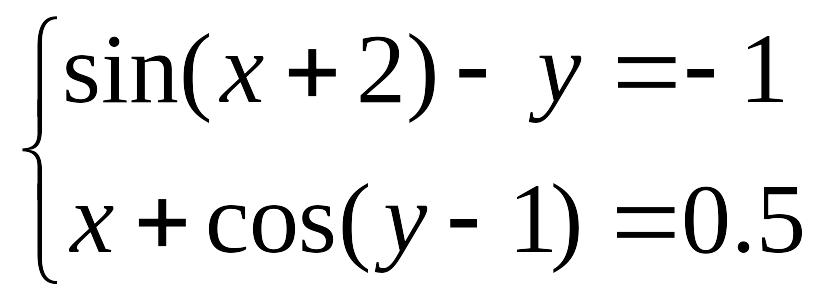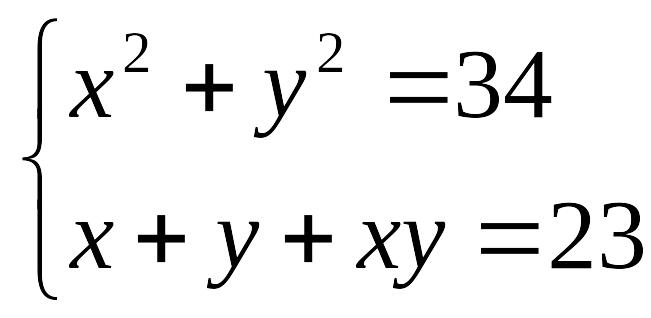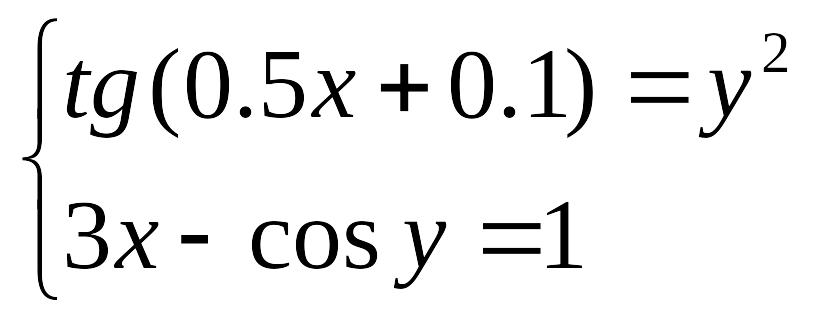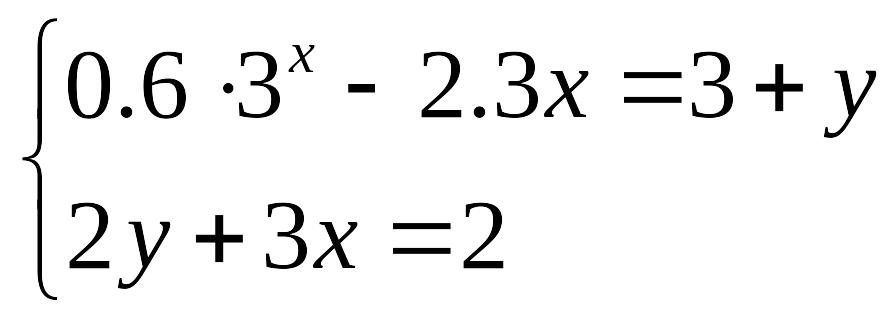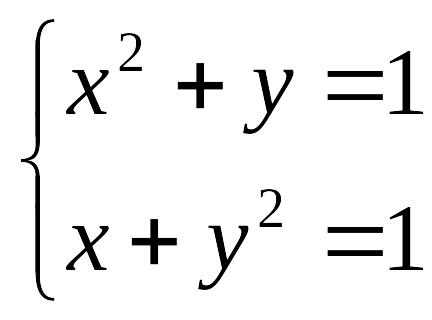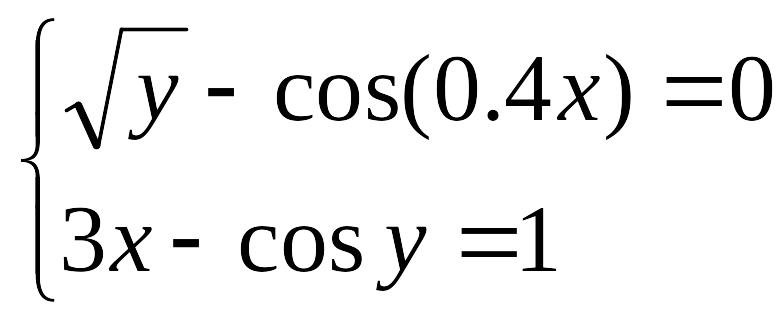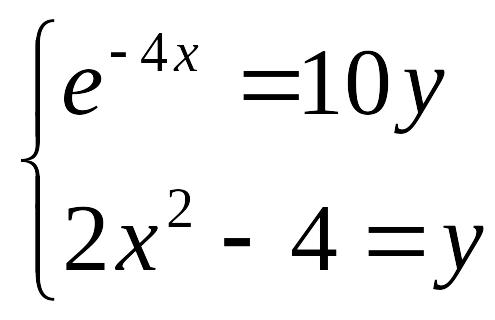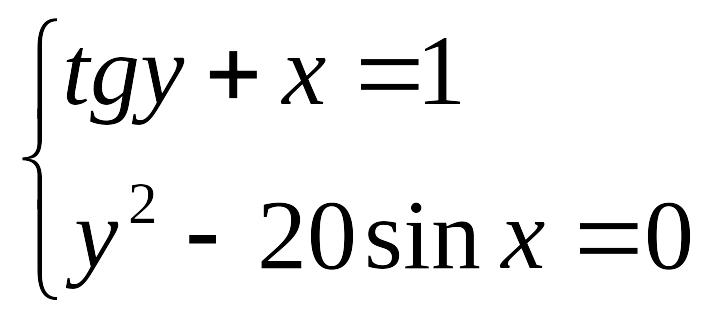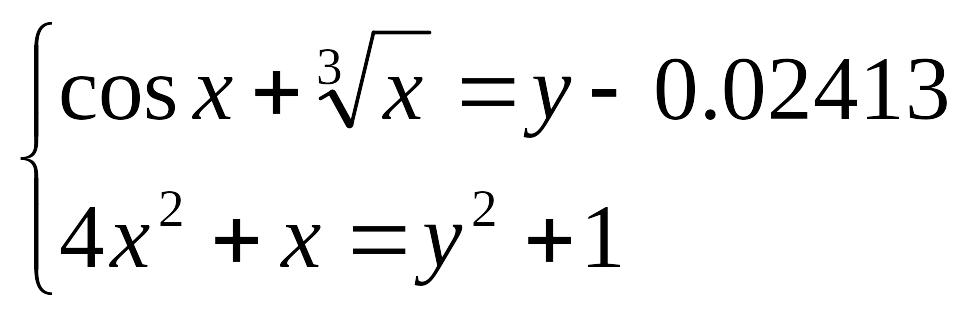- •2.1. Пример выполнения задания 18
- •6.2.1. Варианты заданий по теме: 61
- •Лабораторная работа тема: «Алгебраические и статистические вычисления»
- •Пример выполнения задания по теме: «Алгебраические выражения»
- •Варианты заданий по теме «Алгебраические выражения» [1.1]
- •Пример выполнения задания с использованием статистических функций
- •Варианты заданий по теме «Статистические функции»
- •Лабораторная работа по теме: «Логические вычисления»
- •Пример выполнения задания «Описание геометрического места точек»
- •Варианты заданий по теме «Описание геометрического места точек»
- •Пример выполнения задания по теме «Развилки»
- •Варианты задания по теме «Развилки»
- •Пример выполнения задания по теме «Логические выражения в таблице»
- •Варианты задания по теме «Логические выражения в таблице»
- •Лабораторная работа по теме: «Адресация»
- •Пример выполнения задания по теме «Адресация»
- •Варианты заданий по теме «Адресация»
- •Пример выполнения задания по теме:
- •Лабораторная работа по теме: «Диаграммы»
- •Пример выполнения задания по теме: «Диаграммы»
- •Работа Мастера диаграмм
- •Варианты заданий по теме: «Диаграммы»
- •Коническая
- •Гистограмма
- •Цилиндрическая
- •Лабораторная работа по теме: «»
- •Табулирование функции
- •П ример выполнения задания: «Табулирование функции»
- •Варианты заданий по теме: «Табулирование функции»
- •Решение нелинейного уравнения
- •П ример выполнения задания: «Решение нелинейного уравнения»
- •Решение нелинейного уравнения с помощью подбора параметра.
- •Пример выполнения задания:
- •Варианты заданий по теме: «Решение нелинейного уравнения»
- •Решение системы 2-х нелинейных уравнений
- •П ример выполнения задания:
- •Варианты заданий по теме:
- •Лабораторная работа по теме: «Массивы»
- •Вычисление определителя матрицы и получение обратной матрицы
- •Р ешение матричных уравнений
- •Варианты заданий по теме:
- •Варианты заданий по теме: «Решение матричного уравнения»
- •Решение систем линейных уравнений
- •Вычисление матричных выражений
- •Скалярное произведение векторов
- •Применение скалярного произведения в экономических задачах
- •Варианты заданий «Вычисление скалярного произведения векторов»
- •Варианты заданий: «Решение системы линейных уравнений методом обратной матрицы»
- •Варианты заданий: «Вычисление матричных выражений»
- •Лабораторная работа по теме: «Финансовые функции»
- •Варианты заданий «Простые и сложные проценты»
- •Контрольные вопросы
- •К онтрольные задания
- •Литература
Выполнить команду СервисПодбор параметра.
З аполнить
диалоговое окно команды:
аполнить
диалоговое окно команды:
Установить в ячейке: адрес ячейки, в которой вычисляется f(x);
Значение ввести 0 (нас интересует значение х, при котором f(x)=0);
Изменяя значение ячейки: адрес ячейки-параметра с изменяемым значением – х.
Р
 езультат
выполнения команды выводится в
диалоговом окне «Результат подбора
параметра»:
езультат
выполнения команды выводится в
диалоговом окне «Результат подбора
параметра»:
Если точность решения удовлетворяет заданной – ОК, то в исходные ячейки выводится решение уравнения:
Д
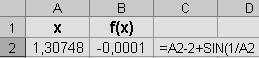 ля
примера 5.3.1. Ответ: х
= 1,3075,
ля
примера 5.3.1. Ответ: х
= 1,3075,
точность решения: 0,0001
Варианты заданий по теме: «Решение нелинейного уравнения»
Решить уравнение f(x) = 0 таблично-графическим способом с точностью
= 0,001. Выполнить проверку методом подбора параметра.
Варианты для функции f(x) взять из 5.1.2 с соответствующими номерами.
Решение системы 2-х нелинейных уравнений
приближённым способом с заданной точностью
Напоминание из курса математики:
Р
 ешением
системы 2-х нелинейных уравнений вида:
F1(x,y)
= 0
ешением
системы 2-х нелинейных уравнений вида:
F1(x,y)
= 0
F2 (x,y) = 0
с неизвестными x и y называется множество значений неизвестных, обращающих одновременно оба уравнения системы в тождества.
Графическим решением системы 2-х нелинейных уравнений являются
координаты (x,y) точки пересечения графиков функций:
y = f1(x) и y = f2(x)
Приближённое решение системы 2-х уравнений состоит из трёх этапов:
определение отрезка оси Ох из области определения функций f1(x) и f2(x), в котором могут быть решения системы;
нахождение грубо приближённых значений решения системы;
уточнение найденных грубых приближений до заданной точности.
Алгоритм решения системы 2-х нелинейных уравнений приближённым
(таблично- графическим) способом с заданной точностью ε:
Отделить решение – установить отрезок [a;b] оси Ох, в котором могут быть решения данной системы.
Протабулировать функции y=f1(x) и y=f2(x) в этом отрезке (см. рис.17).
Построить графики функций по полученным табличным значениям.
В
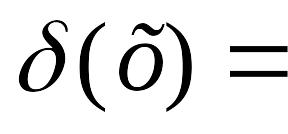 ычислить
f1(x)
- f2(x)
на выбранном отрезке.
ычислить
f1(x)
- f2(x)
на выбранном отрезке.
П![]()
![]() о
таблице значений функций определить
отрезок, на концах которого выражение
принимает значения разных знаков
(в графическом представлении – графики
функций пересекаются). Таким образом,
отрезок содержит значения х,
при которых = 0,
т.е. решение системы.
о
таблице значений функций определить
отрезок, на концах которого выражение
принимает значения разных знаков
(в графическом представлении – графики
функций пересекаются). Таким образом,
отрезок содержит значения х,
при которых = 0,
т.е. решение системы.
Е сли требуемая точность не достигнута, т.е. | | > ε, уточнить решение итерационным способом: задать новые значения а и b, возвратиться к шагу 5). Повторяя этот процесс («итерируя») несколько раз, получить решение системы с заданной точностью, т.е. | | ≤ ε – значение х, удовлетворяющее этому неравенству, и y – одно из значений f1(x) или f2(x), соответствующих этому x.
П ример выполнения задания:
Задание. Решить систему уравнений
таблично-графическим способом с точностью =0,0001.
Выполнить проверку с помощью подбора параметра.
Методические указания к выполнению задания
О
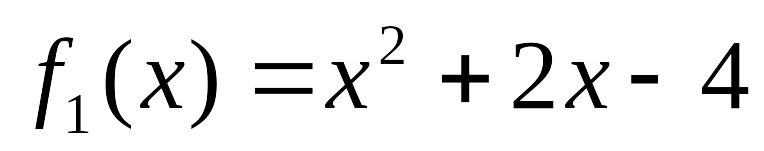 пределить
приближенные значения отрезка Ох, в
котором может быть решение данной
системы. Возьмем отрезок [0;1]. (Отрезок
выбирать исходя из области допустимых
значений х).
пределить
приближенные значения отрезка Ох, в
котором может быть решение данной
системы. Возьмем отрезок [0;1]. (Отрезок
выбирать исходя из области допустимых
значений х).П
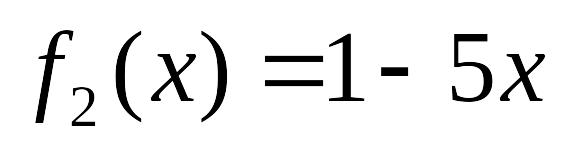
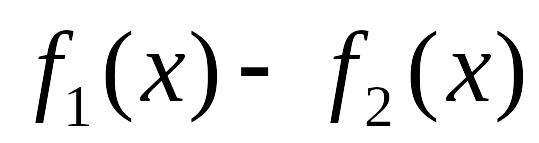 ротабулировать
функции и
в этом отрезке (см. рис.17).
ротабулировать
функции и
в этом отрезке (см. рис.17).Для всех значений аргумента х вычислить .
Построить графики функций по полученным табличным значениям.
И![]() з
графика следует, что функции в отрезке
[0;1] имеют общую точку, т.е. пересекаются,
но разность далека от
заданной точности =0,0001.
з
графика следует, что функции в отрезке
[0;1] имеют общую точку, т.е. пересекаются,
но разность далека от
заданной точности =0,0001.
Р
 ис.17.
Решение системы 2-х нелинейных уравнений
(пример
5.4.1.)
ис.17.
Решение системы 2-х нелинейных уравнений
(пример
5.4.1.)
У точнить решение:
задать значения а=0,6, b=0,7 (в концах этого отрезка разность принимает значения разных знаков);
о братить внимание на изменения в графиках и табличные значения;
наименьшая разность = -0,03;
п олученная точность не удовлетворяет заданной, потому задаем новые значения a=0,65; b=0,66 (рис.17).
в этом отрезке достигается необходимая точность: = 0,0001
решение системы в отрезке [0,65;0,66]: х=0,65330, у=-2,6660 получено за два шага уточнений (итераций).
В ыполнить проверку подбором параметра (СервисПодбор параметра, см.5.3)
п
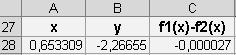 одобрать
=0 для х;
одобрать
=0 для х;вычислить y как y =f1(x) или y =f2(x).
Варианты заданий по теме:
«Решение системы 2-х нелинейных уравнений»
Решить систему нелинейных уравнений с заданной точностью = 0,001. Выполнить проверку с помощью итераций.
№ |
задание |
№ |
задание |
№ |
задание |
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Лабораторная работа по теме: «Массивы»
Цель работы: изучение матричных операций и операций с векторами в Excel, реализуемых с помощью формул массива.
Теоретическая справка. Формулы массива называют также табличными формулами. Формулы массива — очень мощное средство Excel, позволяющее в формулах обращаться с блоком ячеек, как с единым целым. Такие формулы позволяют давать компактные решения сложных задач.
Массивы можно использовать для создания формул, которые возвращают некоторое множество результатов или оперируют множеством значений, а не отдельными значениями.
Формула массива использует
несколько множеств значений,
называемых массивами аргументов,
и возвращает одно или несколько
значений.

Диапазон
массива –
это блок ячеек,
который имеет
общую
формулу
массива
Правила применения формулы массива:
выделить ячейку или диапазон, который будет содержать результаты (диапазон такого же размера и формы, что и диапазон с исходными данными);
ввести формулу вычисления выражения, содержащего массивы аргументов;
нажать Ctrl + Shift + Enter для фиксации ввода формулы массива Excel заключает формулу в фигурные скобки (признак формулы массива).
Примечания.
Редактировать отдельные ячейки массива нельзя. Ячейки в диапазоне массива рассматриваются как единое целое, и редактировать их надо все сразу.
Для изменения или очистки массива следует выделить весь массив и активизировать строку формул. (Фигурные скобки вокруг формулы исчезнут.) Изменить или очистить формулу и нажать Ctrl + Shift + Enter.
Вычисление определителя матрицы и получение обратной матрицы
Задание. Вычислить определитель матрицы А.
Найти матрицу, обратную А.
Примечание. Напоминание из математики по поводу операций с матрицами и векторами здесь и далее не будет, т.к. потребуется более объёмный пояснительный текст. Для воспоминаний отсылаем к [ 5 ].

Рис.18. Выполнение
задания 6.1.
Методические указания к выполнению задания
Ввести в блок В2:D4 исходную матрицу.
Ввести формулу в В6: = МОПРЕД(В2:D4) для вычисления определителя (КатегорияМатематическиеМОПРЕД).
Ввести формулу массива: {=МОБР(B2:D4)} в блок В8:D10 для получения обратной матрицы (КатегорияМатематическиеМОБР).
Варианты заданий по этой теме см. 6.2.1.