ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №2

“СТРУКТУРА РАЗВИЛКА”

В каждом варианте задания необходимо определить требуемые входные и выходные данные , для вычисления предложенных функций составить схемы алгоритмов и программы решения задач. Предусмотреть печать всех входных и выходных данных.

Подготовить контрольные варианты, самостоятельно выбрать значение входных данных, отладить программы.

ВАРИАНТ 1

1. y=

печать значений l и p , если l < p

2. Z₁=

где m = x³

ВАРИАНТ 2

1. y = 0,75z +

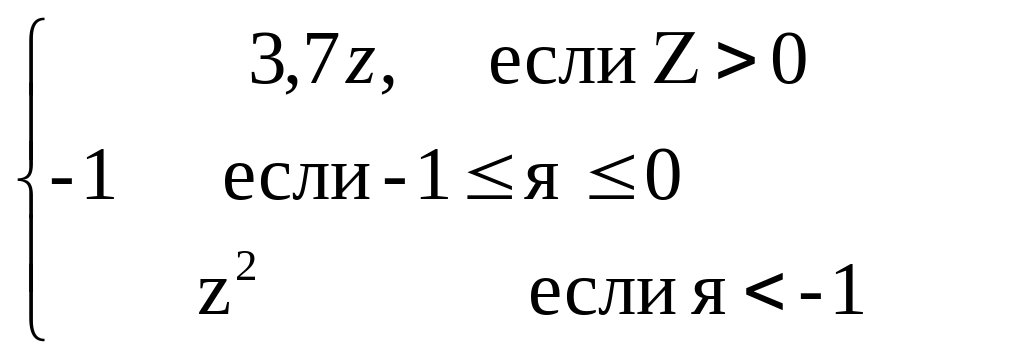
2. q = где к =

ВАРИАНТ 3

1. F = 4,19 + y₁ + y₂, где

2. y =

принять У равным 0, если а < 1

ВАРИАНТ 4

1. z =

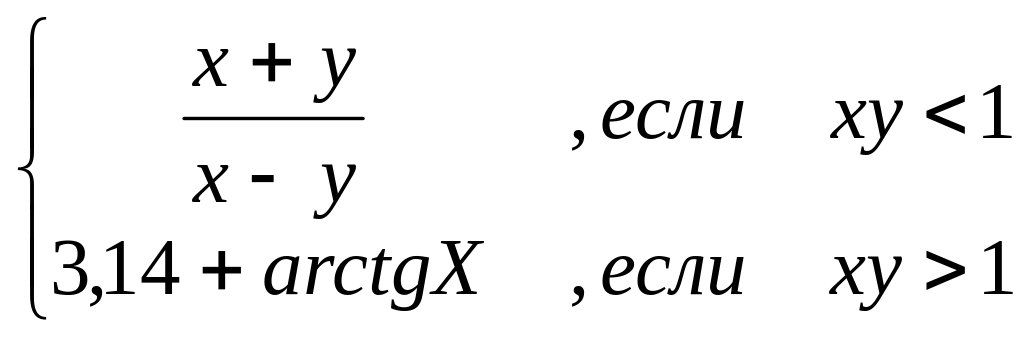
печать значений x и y, если xy = 1

2. Ввести значения r и напечатать c + r, если d

y = 1.5 C²+3.1, если d > 0,

где d = c + 3.25.

ВАРИАНТ 5

1 . g₁ = sinL , g₂ = 1+lg L , если L

g₁ = x⁴+ , если L > 0,5,

где L =

1700 - 0,485x² , если x-120 < 0

2. Y = 0 , eсли x-120 = 0

, если x-120 > 0

Вариант 6

1. y₁= ak² + bk ; y₃ = a + b cosk , если k  10

y₃ = 16,7k + 1,02 , y₁=0 , если k > 10 ,

где k = d - 3

x² - 0,3 , если x < 0

2. L = -407,6  10³ + 0 , если x = 0

x² + 0,3 , если x > 0

Вариант 7

x²ⁿ , если x  0

1. Y =

x ^{2n + 1} , если x < 0, n – натуральное число

(d + b ), z₃ = 1,5 , если a > b

2. Z₂ = a² , если a< b

, если a = b

Вариант 8

1. y = x³ + 3x , если x > 0

y = x³ - 3x , если x  0

2. g₁₌ ; q₂ = 0 , если L > 1

g₁ = , если L < 1

g₁ = , если L = 1

Вариант 9

.

d³ + 1 , если d в интервале 1,10

1. C = , если d < 0

0 , в остальных случаях

x + 5 , если x < 2

2. N = 8,5 + Z₂ , где Z₂ = , если x  2 ,

где x = a - 2,1

Вариант 10

Sinx , если x > 

1. Y = 0 , если  x  

Cosx , если -

, если b  10

2. C = Ln10  Lgb , если b > 10,

где b = qa

Вариант 11

Sinx , если x < 0

1. F = 0 , если 0  x 

Cosx , если x >

2. Y₁ = 1 - 0,5a ; Y₂ = a , если m  3,5

ввести Y₁ и Y₂ , если m > 3,5,

где m = r²

Вариант 12

Lnx , если 2 < x  3

1. Q = d₁ + , где d₁ = Lgx , если x > 4

0. , в остальных случаях

2.

Arctg x , если x > 0

F = ax , если x  0, где а – целое число