4. Обчислимо похідну даної функції:

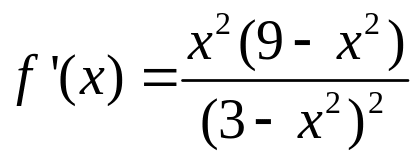. (11)

Визначимо критичні точки I-го роду. Прирівнюючи до нуля чисельник дробу в (11), знаходимо:

х₁=-3; х₂=0; х₃=3. До критичних точок I-го роду відносяться також точки, в яких похідна не існує або дорівнює нескінченності. В прикладі, що розглядається, похідна не існує в точках 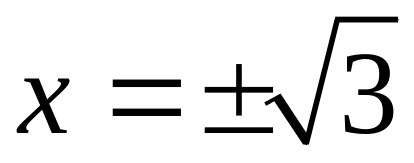(при знаменник відношення (11) обертається в нуль). Але оскільки в цих точках функція не визначена, то вони не являються критичними.

При переході зліва направо через точку х₂=0 похідна не змінює свій знак f ' (-1)0, f ' (1)0. Отже, в цій точці функція не має екстремуму. При переході через точку х₃=3 похідна змінює знак з + на – (f ' (2)0, f ' (4)0), тому точка х₃=3 являється точкою максимуму функції: y_max = f(3)= –4,5.

Для визначення інтервалів зростання та спаду функції необхідно пам’ятати про те, що похідна може змінювати свій знак при переході через точки розриву функції. Враховуючи це, знаходимо, що в інтервалах ( ) та ( ) функція зростає (9–х²>0), а в інтервалі (3;+) – спадає (9-х² 0).

5. Знайдемо

.

Звідси бачимо, що f"(x)=0 тільки при х=0. Точки х= , в яких

f"(x) не існує, не відносяться до критичних точок II роду, бо не належать до області визначення функції. Але при переході через них f"(x) може змінити знак.

При 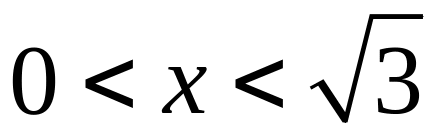f "(x)0 – крива ввігнута ().

При f "(x)<0 – крива випукла ().

При переході через точку х=0 друга похідна f "(x) змінює знак з – на +. Отже, х=0 – абсциса точки перегину графіка. Так як при х=0 f '(x)=0, то дотичною до кривої в точці перегину графіка є вісь абсцис.

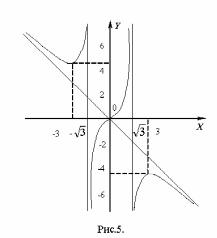
За результатами проведеного дослідження будуємо графік функції для х0 та продовжуємо його симетрично відносно початку координат на підставі п.1 (рис.5).

Література.

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов.-М,:Наука,1970-1978, т.1,2.

2. Задачи и упражнения по математическому анализу для втузов /Под ред. Б.П. Демидовича. – М.:Физматгиз,1956-1963; Наука, 1964-1978.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа,1980. ч.І, ІІ.

4. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов.-М.:Наука,1971. 736 с.

5. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление.-М:Наука,1980,1984.-432 с.

6. Липман Берс. Математический анализ. – М.: Высшая школа., 1975.- 544с.

7. Запорожец Г.И. Руководство к решению задач по математическому анализу. –М.: Высшая школа.,1966.-.479 с.

8. И.А. Каплан. Практические занятия по высшей математике. Части I,V. Издательство Харьковского университета. 1970,1972.

9. Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М. Высшая математика. Линейная и векторная алгебра. Аналитическая геометрия. Введение в математический анализ. Дифференциальное и интегральное исчисление. –К.:Вища школа. Головное издательство, 1987.-552 с.