Правила обчислення похідних

Якщо у – функція від змінної u, а змінна u в свою чергу – функція від змінної х, тобто у=f(u) та u=(x), то функція f((x)) називається функцією від функції або складною функцією. Змінна u в цьому випадку називається проміжним аргументом.

Наприклад, функція у =lntgx є складна функція, оскільки y=ln u, де u = tgx.

Має місце наступна теорема: похідна складної функції у=f(u), де u =(x), по аргументу х дорівнює добутку похідної даної функції у по проміжному аргументу u та похідної проміжного аргумента u по незалежній змінній х, тобто справедлива формула: y’=f’(u) u’.

Покажемо на прикладах, як диференціюється складна функція:

1. .

.

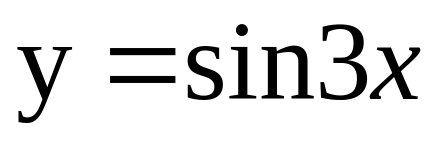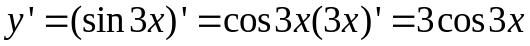2. .

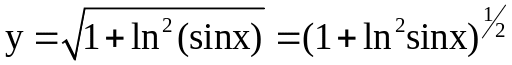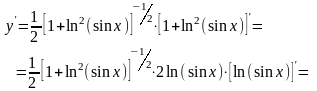
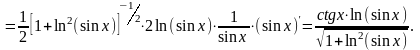
3. .

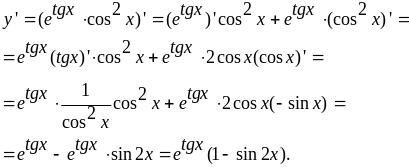
4. .

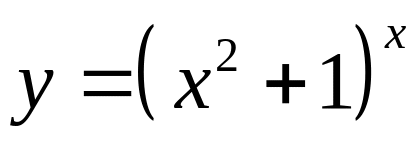Щоб знайти похідну у′ даної функції у=(х²+1)^х, спочатку прологарифмуємо за основою е обидві частини рівності.

lny = xln(х²+1).

Тепер диференціюємо обидві частини отриманої рівності, враховуючи, що lny складна функція змінної х:

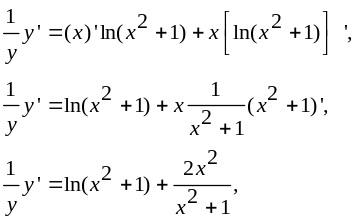
звідки

.

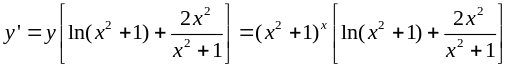Диференціювання функцій, заданих параметрично.

Якщо функція задана параметрично: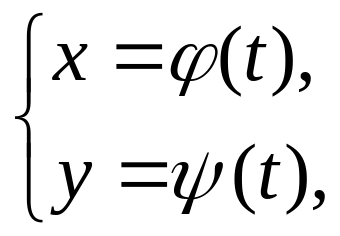 то її похідна у'_x знаходиться за формулою:

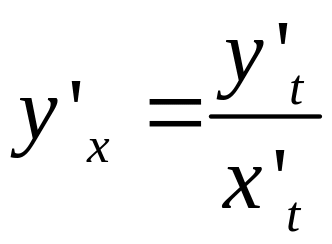, якщо х'_t0.

Приклад. Знайти похідну по незалежній змінній х від функції у, заданої параметрично:

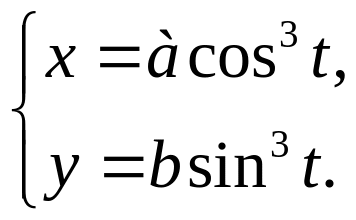
Розв’язання.

.

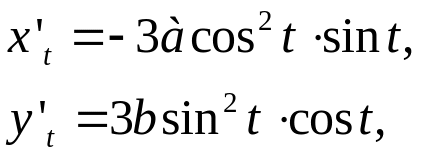
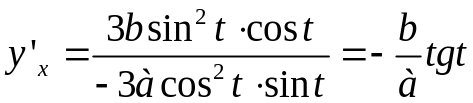Диференціювання неявних функцій

Нехай у є функція від х і зв’язок між х та у задано рівнянням F(x,y)=0; в цьому випадку говорять, що у є неявною функцією від х. Її похідна може бути знайдена з рівняння:

,

де F(x,y)розглядається як складна функція змінної x.

Приклад. Дано функцію 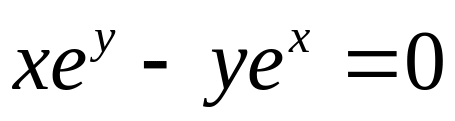, знайти похідну _.

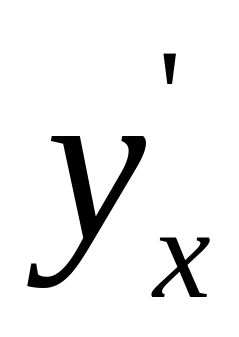Розв’язання. Диференціюючи по х обидві частини рівності та враховуючи, що:

1. у є функція від х;

2. похідна правої частини рівності дорівнює нулю,

отримаємо

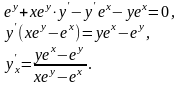
Похідні вищих порядків

Припустимо, що функція у=f(x), має похідну f '(x) на деякому інтервалі змінної х. Похідна від називається похідною другого порядку або другою похідною від первісної функції f(x) та позначається f " (x):

.

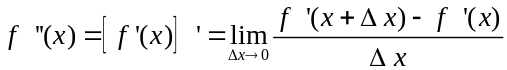Таким чином, похідна n-го порядку f⁽ⁿ⁾(х) від функції у= f(x) називається похідна від похідної (n - 1)-го порядку:

.

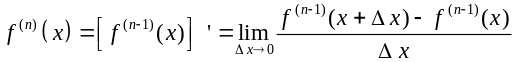Приклад 1. Знайти похідну другого порядку від функції y=cos²2x.

Розв’язання.

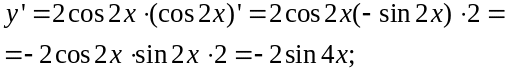
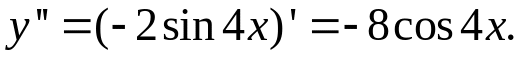
Приклад 2. Знайти похідну другого порядку функції, яку задано параметрично:

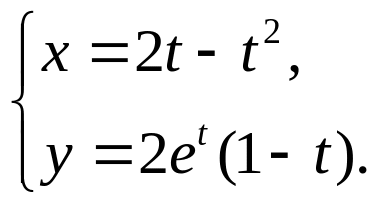
Розв’язання.

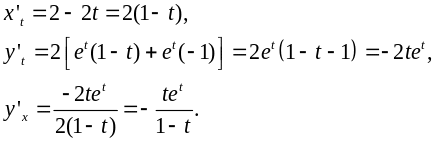
Для похідної другого порядку має місце формула:

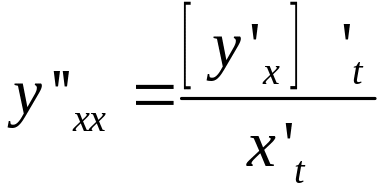або .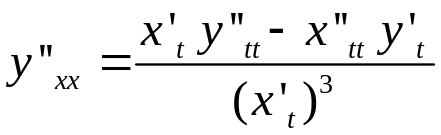

Знаходимо

, ,

.

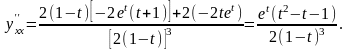7. Дослідження функцій та побудова графіків. Завдання 91-100.

Похідні першого та другого порядків дозволяють дослідити різні властивості функцій. На підставі цих властивостей можна скласти чітку уяву про характерні особливості функції та побудувати математично грамотний ії графік.

Дослідження функції y = f(x) доцільно проводити за наступною загальною схемою.

1. Вияснити область визначення функції D, знайти точки розриву (якщо вони є) та встановити характер поведінки функції біля точок розриву та на границях області D. Корисно також дослідити функцію на парність та непарність, періодичність.

2. Знайти, якщо це не складно, точки перетину кривої y = f(x) з осями координат. Розв’язавши рівняння f(x) = 0, визначити нулі функції f(x) та вияснити її знак в різних інтервалах, враховуючи те, що знак може змінюватись лише при переході через нуль або через точку розриву функції.

3. Якщо область визначення функції D не обмежена, треба вияснити існування асимптот та розташування кривої відносно асимптот. Для існування вертикальної асимптоти необхідно та достатньо, щоб ліміт функції f(x) при наближенні аргументу х до точки розриву х₀ дорівнював нескінченності, тоді х=х₀ – рівняння вертикальної асимптоти. Якщо існують ліміти

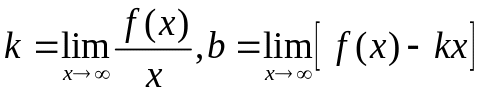, (8)

то крива має похилу асимптоту y = kx + b. При цьому треба розрізняти два випадки: х + та х -. Якщо к=0, а b0, то пряма y = b-горизонтальна асимптота.

4. Знайти критичні точки I роду для функції f(x). Визначивши знак похідної f ' (x) в кожному з проміжків між двома сусідніми критичними точками, визначити інтервали зростання та спадання функції та її екстремуми.

5. Знайти критичні точки II роду для функції f(x). Вияснити знак f " (x) в кожному з проміжків між двома сусідніми критичними точками, встановити інтервали випуклості та ввігнутості функції та точки перегину графіка.

За результатами дослідження будується графік функції у=f(x). Побудову кривої рекомендується почати з нанесення на площину її асимптот і характерних точок (граничні точки області визначення функції, точки розриву, перетину графіка з осями координат, екстремуму, перегину графіка). Іноді для більш точного зображення кривої знаходять значення функції в деяких допоміжних точках. Знаючи інтервали зростання та спадання функції, а також інтервали випуклості та ввігнутості, можна правильно нарисувати криву. В тому випадку, коли f(x) – парна, непарна чи періодична функція, побудова графіка функції спрощується: графік парної функції є симетричний відносно осі ординат, а непарної – відносно початку координат, графік періодичної функції повторюється через рівні відрізки осі абсцис.

Проілюструємо застосування викладеної методики дослідження функції.

Задача 13. Дослідити функцію 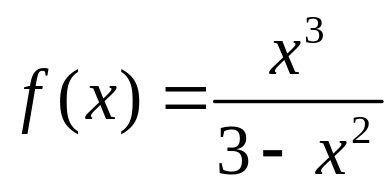та побудувати її графік.

Розв’язання. Функція представлена відношенням двох многочленів, тому вона визначена та неперервна скрізь на числовій осі, крім точок 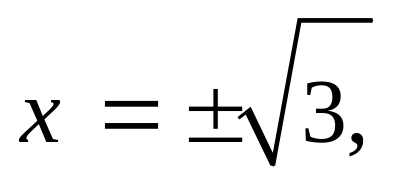в яких знаменник дорівнює нулю, тобто . Функція непарна, так як

.

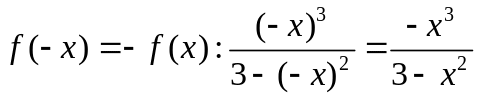Отже, її графік симетричний відносно початку координат. Це дозволяє обмежитись дослідженням функції тільки при х0. Іншу частину графіка побудуємо, користуючись його симетрією.

Функція не являється періодичною, оскільки для всіх х є D рівність 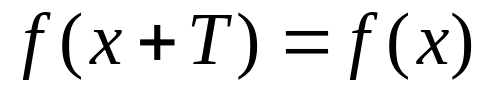виконується тільки при Т = 0.

Знайдемо граничні значення (на границі області D).

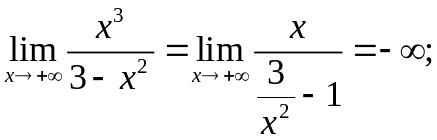
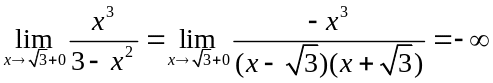; (9)

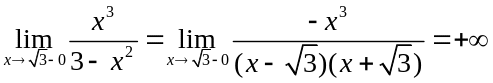. (10)

2. Якщо х=0, то f(x)=0, тобто графік функції проходить через початок координат. Інших точок перетину кривої з осями координат немає. Інтервали, в яких функція зберігає знак, такі:

якщо 0х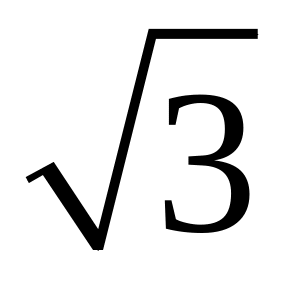 , то y = f(x)  0;

якщо х , то y = f(x)  0.

3. З умов (9), (10) видно, що пряма х= є вертикальна асимптота. Вияснимо питання про існування похилої асимптоти. За формулами (8) знайдемо k та b:

,

.

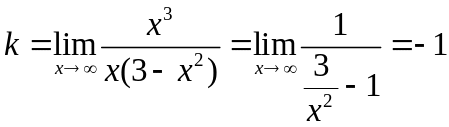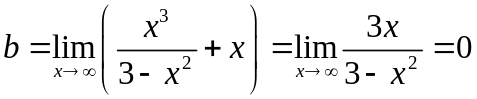Отже графік функції має асимптоту у = –х. Для того, щоб зробити висновок про взаємне розташування кривої та асимптоти, розглянемо різницю

.

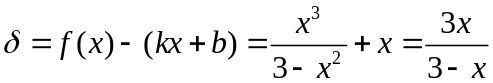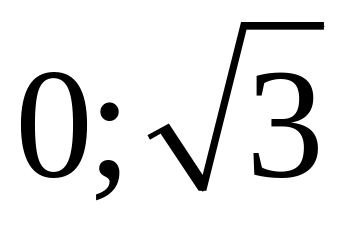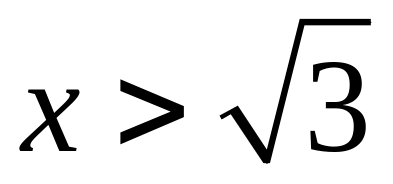Звідки   0, якщо х 0 і 3 – х²  0, тобто в інтервалі ( ) крива повинна знаходитися над асимптотою (нагадаємо, що нас цікавить тільки значення х0). Аналогічно знаходимо, що 0, при , і в цьому інтервалі крива розташована під асимптотою. В точці х=0 =0, отже асимптота перетинається з кривою.