39

Контрольна робота № 2. Завдання №№ 51-60, 61-70, 81-90, 91-100.

4. Знаходження границь функцій

Завдання 51-60.

Перед тим, як шукати границі, важливо засвоїти поняття границі (ліміту) змінної величини, границі (ліміту) функції та способи їх знаходження.

Стале число а називається границею (лімітом) змінної величини х, якщо для будь-якого додатного числа 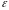абсолютне значення різниці х-а, починаючи з деякого моменту, стає та в подальшому буде залишатися меншим, ніж ε:

|x-a|<ε . (6)

Це можна записати так: хa (x наближається до а), або lim x=a (ліміт х дорівнює а).

Геометрично стала величина а зображується фіксованою точкою на числовій осі, а змінна х – рухомою точкою.

Якщо стала а є границею змінної х, то геометрично це означає, що точки, які зображують х, починаючи з деякого моменту, попадуть всередину проміжку довжиною 2ε з центром в точці а, і в подальшому всередині цього проміжку будуть залишатися.

Очевидно, що при цьому буде виконуватись нерівність (6). Змінна величина  називається нескінченно малою, якщо її границею є число нуль. Записують: || ε , або ε , або lim =0.

Змінна величина х називається нескінченно великою, якщо яким би не було, нехай і дуже великим, додатне число М, серед значень х завжди знайдуться такі, що для них буде виконуватись нерівність:

|x| М.

Це записується в вигляді: х, (х прямує до нескінченності), або

lim х=.

Між нескінченно великими та нескінченно малими існує зв’язок: величина, обернена до нескінченно малої, є нескінченно велика, та, навпаки, величина, обернена до нескінченно великої, являється нескінченно малою. Символічно це можна записати в вигляді:

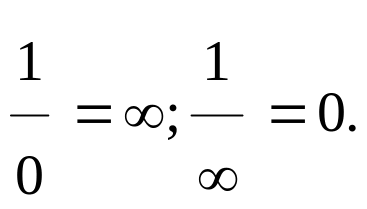
Стале число А називається границею (лімітом) функції y=f(x) в точці х=а, якщо абсолютне значення різниці f(x)-А стає меншим, ніж будь-яке наперед задане додатне число ε, нехай і як завгодно мале, як тільки |x-а| буде меншим від деякого достатньо малого додатного числа 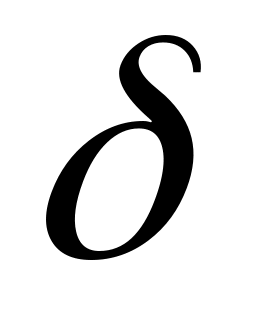, яке, взагалі говорячи, залежить від ε.

Це можна записати: f(x)А при ха, або .

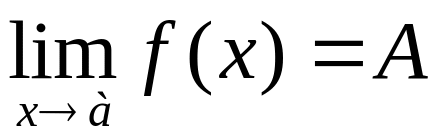При знаходженні границь функцій треба користуватися наступними теоремами про границі:

1. Границя (ліміт) алгебраїчної суми двох змінних дорівнює алгебраїчній сумі границь цих змінних

lim (xy)=lim x lim y, якщо останні існують.

2. Ліміт добутку дорівнює добутку лімітів цих змінних

lim (xy)=lim x lim y, якщо останні існують.

3. Ліміт частки від ділення двох змінних дорівнює частці від ділення лімітів цих змінних

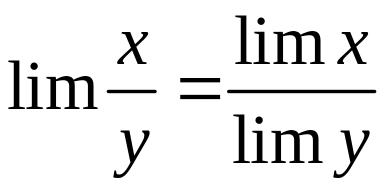, якщо останні існують і, якщо ліміт знаменника не дорівнює нулю.

При знаходженні границь (лімітів) функції можуть зустрітися сім видів невизначеності:

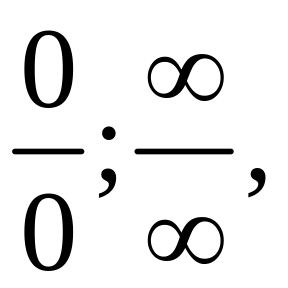0. , -, 0⁰ , ⁰, 1^.

Розкриваються вказані невизначеності або за допомогою алгебраїчних чи трансцендентних перетворень долімітних виразів, або використанням уже відомих лімітів

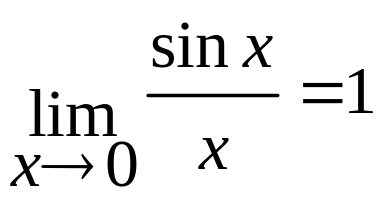
та

, (7)

де е=2,718281828459045... – ірраціональне число, а також використовуючи наслідки останніх формул, наприклад

,

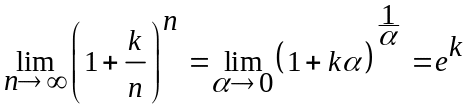де к = const.

При розкритті невизначеностей виду 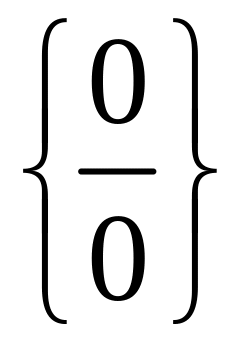іноді ефективно застосовувати теореми про еквівалентні нескінченно малі функції.

Дві нескінченно малі функції називаються еквівалентними, якщо ліміт їх відношення дорівнює одиниці. Це записується символічно так:

(х) (x).

Теорема: ліміт відношення двох нескінченно малих функцій дорівнює ліміту відношення еквівалентних їм функцій.

Корисно пам'ятати такі еквівалентні нескінченно малі функції при 0 та m=const:

sinmm, tgmm, arcsinmm, arctgmm, ln(1+m)m, e^m - 1m, a^m –1mlna,  .

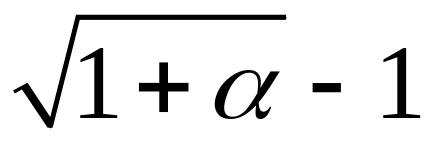
Розглянемо декілька типових задач на знаходження лімітів.

Знайти границі, не користуючись правилом Лопіталя.

Задача 6. Знайти

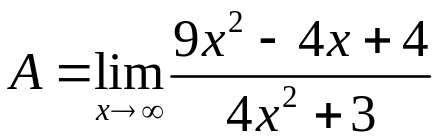
Розв’язання. При х і чисельних 9х² – 4х + 4 і знаменник 4х²+3 безмежно збільшуються. В цьому випадку ми маємо невизначеність виду . Для розкриття невизначеності тут рекомендується поділити чисельник і знаменник долімітного виразу на найвищий степінь х, у нас – на х². А потім застосовуємо теорему про границі та отримуємо:

Задача 7. Знайти

.

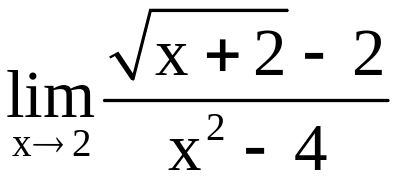Розв’язання. При х2 чисельник і знаменник прямують до нуля, тобто ми маємо невизначеність виду . Щоб розкрити цю невизначеність, треба позбавитись від ірраціональності в чисельнику, для чого помножимо чисельник і знаменник на вираз :

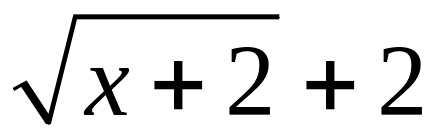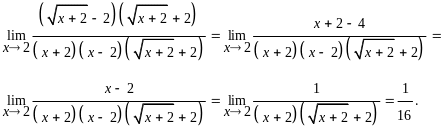
Задача 8. Знайти

.

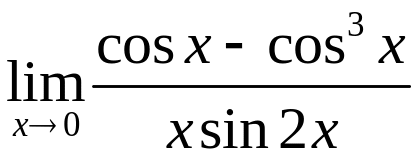Розв’язання. При х0 чисельник і знаменник прямують до нуля.

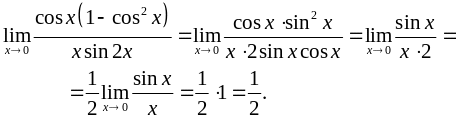
Задача 9. Знайти

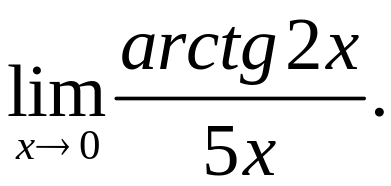
Розв’язання.

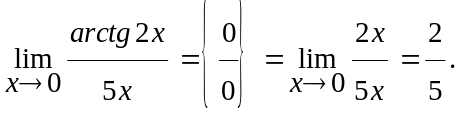
Тут ми врахували, що при х0 arctg2x2x, та застосували теорему про еквівалентні нескінченно малі функції.

Задача 10. Знайти

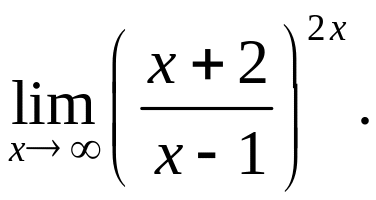
Розв’язання. При х основа степеня 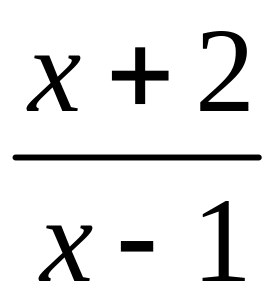прямує до одиниці

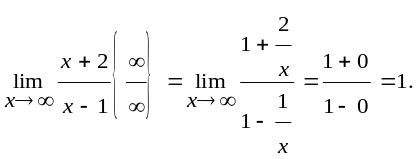
Тобто ми маємо невизначеність виду {1^}.

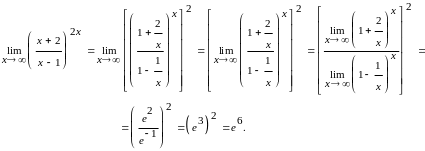
Тут ми застосували формулу (7).

Задача 11. Знайти

.

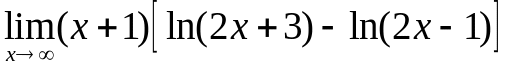Розв’язання. При х в квадратних дужках маємо невизначеність виду { -}.

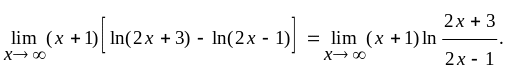
При х . Дійсно

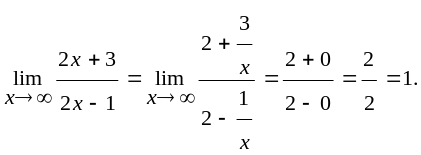
Отже, знову маємо невизначеність виду {, 0}, оскільки ln1=0.

Продовжимо перетворення:

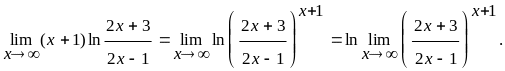
Тепер ми маємо невизначеність виду {1^}.

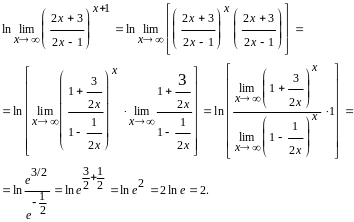
Тут знову застосували формулу (7).