23

Зміст

1. Розв’язування систем лінійних рівнянь. Завдання 1-10………..4

2. Елементи векторної алгебри та аналітичної геометрії.

Завдання 11-20……………………………………………………..8

Завдання 21-30…………………………………………………….9

Завдання 31-40…………………………………………………….15

3. Побудова ліній в полярній системі координат.

Завдання 41-50……………………………………………………..19

4. Знаходження границь функцій. Завдання 51-60………………...22

5. Неперервність функції. Точки розриву. Завдання 61-70……….27

6. Похідна. Завдання 71-80, 81-90…………………………………29

7. Дослідження функцій та побудова графіків.

Завдання 91-100……………………………………………………34

Література………………………………………………………….38

Контрольна робота № 1.

Завдання №№ 1-10, 11-20, 21-30, 31-40, 41-50.

1. Розв’язування систем лінійних рівнянь.

Завдання 1-10.

Задача 1. Довести сумісність даної системи лінійних рівнянь та розв’я-зати її трьома способами:

1. методом Гауса;

2. засобами матричного числення;

3. за допомогою формул Крамера.

Розв’язання. Обчислимо визначник системи

Оскільки визначник системи   0, то надана система сумісна і має тіль-ки один розв’язок.

1) Розв’яжемо систему методом Гауса. Для цього виберемо одне рівнян-ня системи, наприклад, перше, як ведуче.

За допомогою ведучого рівняння виключимо х₁ з другого та третього рівнянь. Для цього помножимо перше рівняння на –2 та складемо його з другим; потім помножимо перше рівняння на –1 і додамо його до третього. Одержимо систему

Тепер розглянемо підсистему, яка складається з другого та третього рівнянь. Друге рівняння приймаємо як ведуче та х₂ приймаємо за друге ведуче невідоме. За допомогою цього другого рівняння виключаємо х₂ з третього рівняння. Для цього помножимо друге рівняння на 1/5 та складемо його з третім. Отримаємо систему:

Залишилось знайти розв’язок. З третього рівняння маємо х₃=2. Потім з другого рівняння знаходимо

.

І, нарешті, з першого рівняння отримуємо

х₁ = –2х₂–3х₃+5=2–6+5=1.

Відповідь: система має тільки один розв’язок

х₁ =1, х₂ = –1, х₃ = 2.

2) Розв’яжемо дану систему засобами матричного числення.

Випишемо матрицю, що складається з коефіцієнтів при невідомих

,

яка називається матрицею системи, матрицю – стовпець, що складається з невідомих

,

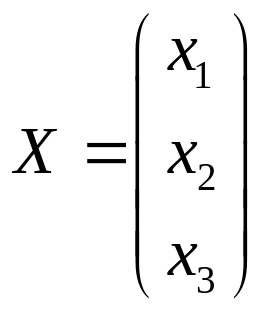та матрицю – стовпець, що складається з вільних членів

.

Якщо помножити матрицю А на матрицю Х, то отримаємо матрицю-стовпець, яка складається з лівих частин заданої системи рівнянь.

.

Таким чином, наша система рівнянь може бути переписана в наступному матричному вигляді

АХ=В.

Помножимо цю рівність на матрицю А^-1, обернену до матриці А, будемо мати

А^-1АХ= А^-1В.

Але, за визначенням, А^-1А=Е, де Е– одинична матриця

.

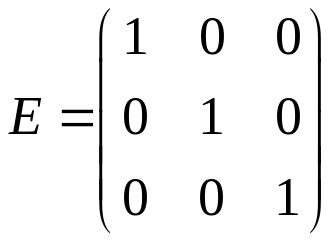Тоді остання рівність набуває вигляду

EX=A^-1B,

або, оскільки EX = X, то

Х=А^-1В.

Звідси випливає, що треба знайти матрицю А^-1, обернену до матриці А, помножити її на матрицю-стовпець В, який складається з вільних членів, і ми отримаємо матрицю-стовпець, складену з шуканих невідомих.

Обернену матрицю знаходимо за формулою

,

де =2 – вже обчислений нами визначник матриці даної системи, а А_ik – алгебраїчне доповнення елемента а_ik матриці А, що стоїть на перетині і-того рядка та к-го стовпця.

Обчислимо всі алгебраїчні доповнення

; ;

; ;

; ;

;

.

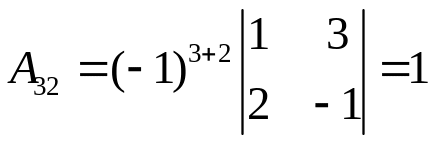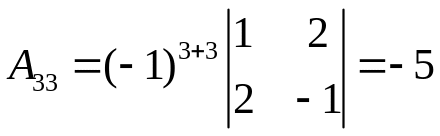Тепер можна виписати обернену матрицю

.

Для того, щоб перевірити вірність знайденої оберненої матриці А^-1, помножимо її на матрицю А, одержимо матрицю Е:

= .

Залишилось помножити матрицю А^-1 на матрицю В. Одержимо шуканий розв’язок:

.

Таким чином, одержимо відповідь: система має єдиний розв’язок

х₁= 1, х₂= -1, х₃= 2.

2. Елементи векторної алгебри та аналітичної геометрії.

Завдання 11-20.

Задача 2. Задано чотири вектора та у деякому базисі. Показати, що вектори утворюють базис, та знайти координати вектора у цьому базисі.