За умови дисконтування m разів на рік використовують номінальну облікову ставку f. У кожному періоді дисконтування здійснюється за ставкою f/m:
P = S (1 – f/m)mn,
де mn — загальна кількість періодів дисконтування.
Під ефективною обліковою ставкою розуміють складну річну облікову ставку, еквівалентну номінальній за заданого значення кількості дисконтувань на рік:
Ефективна облікова ставка менша за номінальну.
Нарощення за складною обліковою ставкою визначають так:
;
Знаходження процентних ставок
1. Для простої процентної ставки:
2. У разі нарощення за складною річною ставкою:
3. У випадку нарощення за номінальною ставкою процентів m разів на рік:
4. За умови дисконтування за простою обліковою ставкою:
5. У разі дисконтування за складною обліковою ставкою:
6. У випадку дисконтування за номінальною обліковою ставкою m разів на рік:
Визначення строку позички
1. За простою ставкою процентів:
2. За складною ставкою процентів:
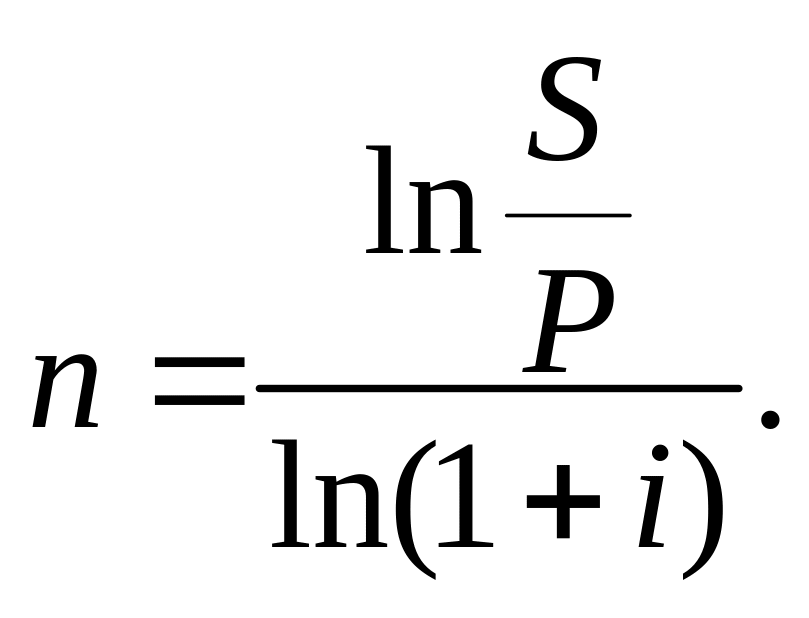
3. У разі нарощення за номінальною ставкою процентів j/m разів на рік:
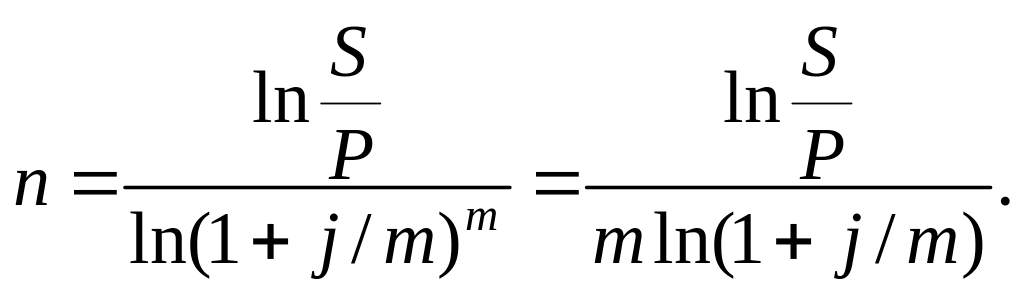
4. У випадку дисконтування за простою обліковою ставкою:
5. За умови дисконтування за складною обліковою ставкою:
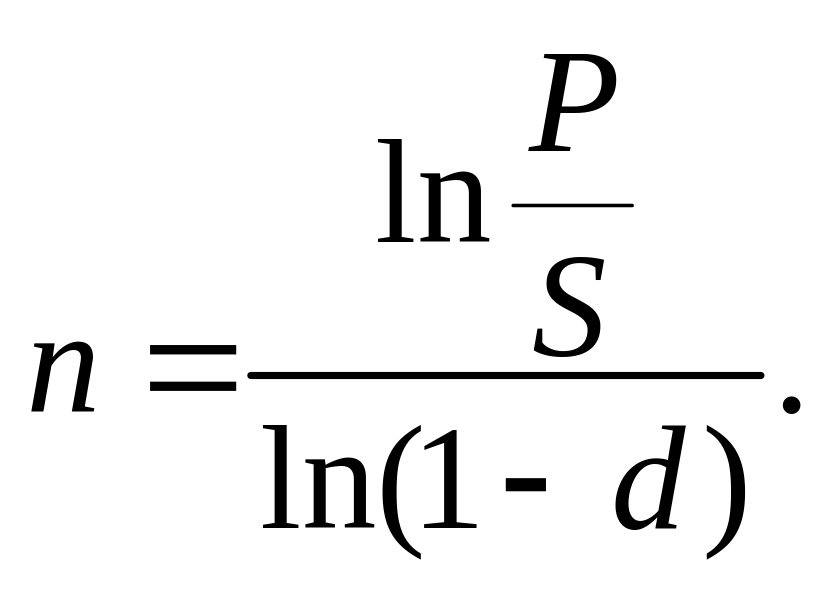
6. У разі дисконтування за номінальною обліковою ставкою m разів на рік:
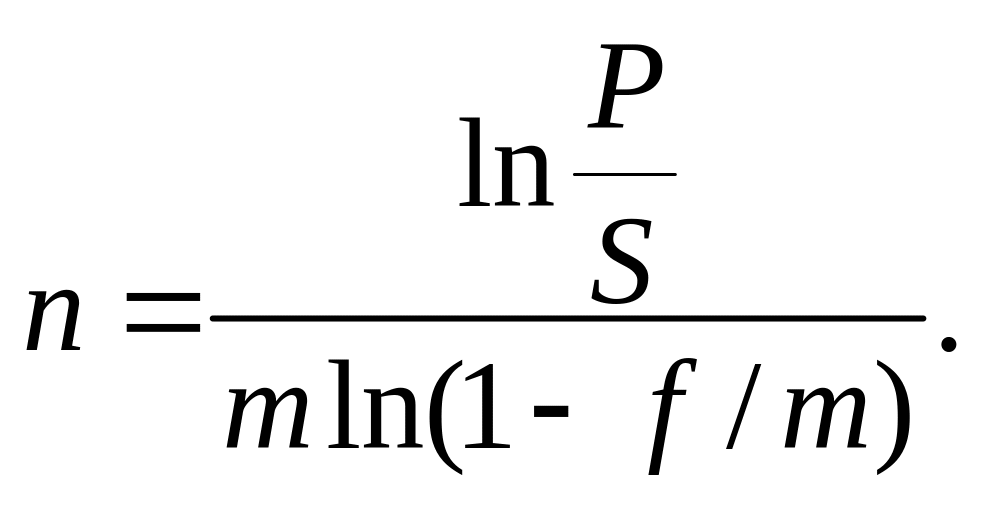
Урахування інфляції здійснюють у розрахунках таким чином. Основним показником, що характеризує динаміку інфляційних процесів, є індекс купівельної спроможності грошей. Тоді
,
де
— реальна нарощена сума; S —
нарощена сума за n
років.
,
де — темп інфляції.
,
— реальна нарощена сума з урахуванням темпу інфляції.
Приклади розв’язання задач до теми Задачі на розрахунок складних процентів
1. Розрахуйте, що вигідніше для вкладника: отримати 20 000 грн сьогодні або отримати 35 000 грн через 3 роки, якщо процентна ставка дорівнює 17%.
Розв’язання:
Розрахуємо майбутню вартість 20000 грн через 3 роки зі ставкою 17% річних.
FV = 20000 ∙ (1 + 0,17)3 = 32032 грн.
Отже, отримати 35000 грн через 3 роки вигідніше за такого значення процентної ставки.
2. Визначити, скільки років буде потрібно для того, щоб сума в 1000 грн, покладених в банк, зросла до 20000 грн, якщо процентна ставка дорівнює 14% річних.
Розв’язання:
Перетворимо формулу для розрахунку складних процентів до такого вигляду:
(1 + r) n = FV / PV і підставимо значення;
1,14n = 20000 / 1000 = 20, звідси, n = log 1,14 20 = 22,86 року.
Отже, 1000 грн збільшиться до 20000 грн за 14%-ї річної ставки за 22,86 року.
У процесі розрахунку кількості років необхідно враховувати, що у формулі мається на увазі ціла кількість років і цифри, що розраховуються після коми, мають приблизні значення і характеризують близькість до цілого значення років.
3. Якою має бути ставка позикового процента, аби сума в 10 000 грн зросла до 30 000 грн за термін вкладу 5 років?
Розв’язання:
Перетворимо формулу для розрахунку складних процентів до такого вигляду:
r = (FV / PV)1/n - 1 і підставимо значення;
r = (30 000 / 10 000)1/5 - 1;
r = 0,24573 або 24,573 %.
Тобто, 10 000 грн зростуть до 30 000 грн за 5 років, якщо ставка позикового процента дорівнюватиме 24,573% .