Кінцеві вартості: початкова сума 1000 грн, ставка позикового процента 4, 12, 20, 28% річних

Для оцінки руху фінансових потоків в часі також застосовують розрахунок приведеної вартості або метод дисконтованих грошових потоків.

Дисконтування є операцією, оберненою до операції розрахунку складних процентів. У той час коли інфляція більше нуля, гроші на дійсний момент часу коштують дорожче, ніж на майбутнє. Для того щоб визначити сьогоднішню вартість грошей і застосовують дисконтування грошових потоків.

Сутність розрахунку полягає в тому, що плановані грошові надходження перераховують у сьогоднішню вартість з врахуванням кількості періодів і ставки дисконтування за формулою, оберненою до розрахунку складних процентів.

Наприклад, плановані 1000 грн через 1 рік інвестування за ставки дисконтування 15%, еквівалентні сьогоднішнім 869,57грн; через 2 роки – 756,14 грн.; через 3 роки –657,52 грн.

У даному прикладі величина 869,57 грн є поточною вартістю величини 1000 грн, отриманих від інвестиції строком на 1 рік за ставки дисконтування 15%.

Формула для розрахунку дисконтованого грошового потоку така:

PV = FV/ (1 + r) ⁿ,

де FV – майбутня вартість; PV – поточна вартість; r – ставка дисконтування; n – кількість років.

Чим довший термін отримання доходу від інвестиції і чим вища процентна ставка дисконтування, тим менша поточна вартість (рис. 3).

Грн

Роки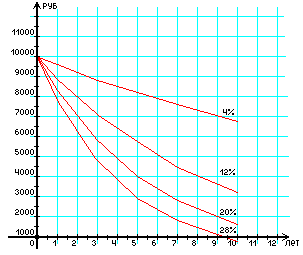

Рис. 3. Графік приведеної вартості;

Поточні вартості: початкова сума 10000 грн, ставка дисконтування 4, 12, 20, 28% річних

Якщо передбачаються зміни у часі, але застосовано фіксовані (змінні) ставки процентів, то формула нарощення за складними процентами матиме такий вигляд:

S = P (1 + i₁)ⁿ¹(1 + i₂)ⁿ²… (1 + i_k)^nk,

де i₁, i₂,..., i_k — послідовні значення ставок процентів;

n₁, n₂,...,n_k — періоди, протягом яких здійснюється нарахування за відповідними ставками.

Загальний випадок, коли необхідно визначити число років, протягом яких початкова сума збільшиться в N разів:

а) для простих процентів (1 + ni_n) = N; ;

б) для складних процентів (1 + i_c)ⁿ = N; .

Для N = 2;

а) подвоєння за простими процентами:

б) подвоєння за складними процентами:

.

У випадках, коли n не ціле число, тобто складається з цілої й дробової частин, нарощення визначають двома способами: за формулою нарощення складних процентів і на основі змішаного методу, згідно з яким за ціле число років нараховують склад­ні проценти, а за дробове — прості:

S = P (1 + i)^a(1 + bi),

де n = a + b, a — ціле число років, b — дробова частка року.

Для m разів нарахування процентів на рік нарощену суму визначають за формулою:

S = P (1 + j/m)^mn.

Ефективну ставку процентів визначають за такою формулою:

I = (1 + j/m)^m – 1.

Якщо необхідно визначити на основі ефективної номінальну ставку, то можна застосувати таку формулу:

j = m ((1 + i)^1/m – 1).

Розрізняють два методи дисконтування — математичне дисконтування і банківський облік.

Математичне дисконтування застосовують у тих випадках, коли за заданими S, n та i необхідно знайти P:

,

де — множник дисконтування.

Величину P, якщо вона визначена за S, називають дисконтованою величиною S, або сучасною величиною платежу S, або теперішньою вартістю.

Величину V ⁿ називають обліковим або дисконтованим множником.

Якщо проценти нараховують m разів на рік, формула матиме такий вигляд:

.

Дисконтний множник дорівнює

.

Дисконтування за складною обліковою ставкою здійснюють за формулою:

P = S (1 – d_c)ⁿ,

де d_c — складна облікова ставка;

S — сума майбутніх платежів, на яку нараховують процентну ставку;

(1 – d_c)ⁿ — множник дисконтування.

Дисконт у такому разі:

D_d = S – S (1 – d_c)ⁿ = S (1 – (1 – d_c)ⁿ).