Приклади розв’язання задач до теми

1. Сума кредиту, виданого на строк 2 роки під 5 % річних — 1000 грн. Визначити процент, який отримує кредитор, та суму, яку боржник виплатить наприкінці строку.

Розв’язання:

Спочатку визначимо величину процента:

І = P · i · n = 1000 · 0,05 · 2 = 100 грн,

а потім нарощену суму S = P + I = 1000 + 100 = 1100 грн.

Цю задачу можна розв’язати також іншим способом:

S = P(1 + n · i) = 1000 (1 + 2 · 0,05) = 1100;

I = S – P = 1100 – 1000 = 100 грн.

2. Яка буде нарощена сума позички, якщо угодою передбачено за перші два роки нарахування 10 % річних, а в наступні два роки ставка простих процентів збільшуватиметься кожні півроку на 1 процентний пункт. Початкова сума позички — 1000 грн.

Розв’язання:

3. Визначити суму, яку видасть кредитор і суму дисконту, якщо через три місяці з моменту видачі кредиту боржник сплатить кредитору 1025 грн. Кредит надано під 10 % річних.

Розв’язання:

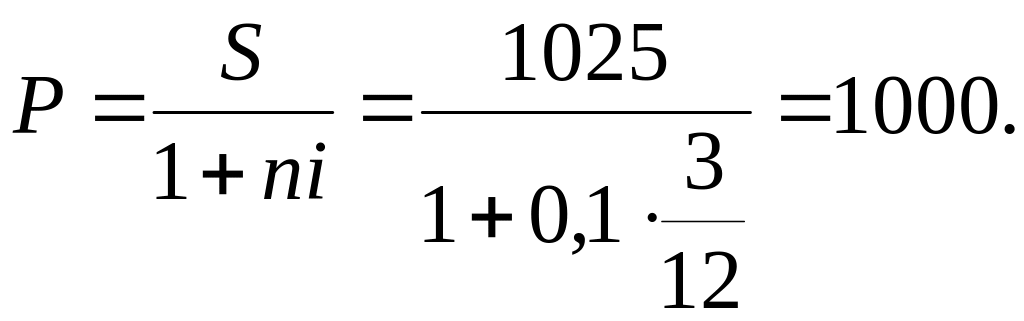
Величина дисконту D = S – P = 1025 – 1000 = 25 (грн).

4. Знайти під час обліку векселів суму, яку банк виплатить власнику, якщо останній врахував його в банку 15 жовтня. Вексель було надано на суму 1000 грн. з оплатою 15 листопада. Облікова ставка 10 %.

Розв’язання:

З цієї суми банк може утримувати і комісійні за проведення операції.

5. Визначити суму, яку потрібно поставити в бланку векселя за умови, що строк векселя 3 місяці, облікова ставка — 10 %, під вексель надано 1000 грн.

Розв’язання:

6. Визначити, яку облікову ставку застосував банк, заплативши 1240 грн під час обліку векселя, викупна ціна якого 1300 грн. Термін платежу за векселем настає через 4 місяці.

Розв’язання:

7. Сума кредиту 1000 грн. Процентна ставка 10 % річних. Нараховують прості проценти. У кінці строку боржник поверне суму в розмірі 1040 грн. Необхідно визначити, на який строк надано цей кредит.

Розв’язання:

Завдання та запитання для самостійної роботи

1. Виведіть формули для обчислення нарощеної суми за схемою простих позичкових процентів для різних випадків задавання процентних ставок і процентних періодів.

2. Виведіть формули для обчислення нарощеної суми за схемою простих авансових процентів для різних випадків встановлення процентних ставок і процентних періодів.

3. Дайте визначення поняття «дисконтування за простою процентною ставкою» і напишіть усі можливі формули для позичкових процентів.

4. Напишіть усі можливі формули для обчислення дійсної вартості майбутніх грошей для авансових про­центів.

5. Чим відрізняється нарощення грошей від компаудингу?

6. Розрахуйте, застосовуючи англійський метод, якою буде сума на депозитному рахунку через 47 днів, якщо на неї нараховують прості проценти виходячи з річної про­центної ставки 30%. Початковий внесок складає 3 тис. грн.

7.1 січня 2012 р. (високосний рік) на депозитний внесок помістили 5 тис. грн під 20% річних. Розрахуйте нарощену суму грошей через 5 міс., застосовуючи англійську, французьку і німецьку схеми нарахування процентів.

8. Визначте на підставі річної ставки прибутковості, що вигідніше для вкладника, який має суму 1 тис. грн, — віддати її на 6 міс., розраховуючи одержати 1700 грн, або на 8 міс., плануючи одержати 1800 грн.

9. Визначте прибутковість до погашення і поточну при­бутковість операції купівлі ОВДП номіналом 1000 грн, якщо на момент випуску облігації продавалися за ціною 700 грн, а через 2 міс. — по 850 грн. Термін погашення настане через 8 міс.

10. Розрахуйте нарощену суму грошей, якщо початко­ва сума 1000 грн. Банк на неповний рік нараховує прості проценти: перші 5 міс. — 10% на місяць, наступні 2 квар­тали — 20% за квартал і останнє півріччя — 30% за півріччя.

11. Визначте нарощену суму грошей, якщо початкова сума внеску 1000 грн, протягом 5 міс. нараховувалися авансові проценти (10% річних), далі протя­гом 2 місяців нараховувалися позичкові проценти (30% річних) і, нарешті, протягом останніх 45 днів — 24% річних.

12. Курс акцій на 1 березня 2012 р. складає 50%. Виз­начте прибутковість вкладення грошей в акції, якщо дата погашення акцій 1 жовтня 2012 р.

13. Яку суму грошей потрібно вкласти на півроку під 18% річних, щоб одержати 12 тис. грн?

14. Відомо, що акції фірми банк купує за ціною 350 грн, дисконтна ставка — 40% річних, а дата погашення на­стає через 1 місяць. Визначте номінал цього цінного папе­ра.

15. Річна ставка простих процентів — 12,5%. Через скільки років початкова сума подвоїться?

16. Вексель на суму 200 тис. грн містить зобов'язання виплатити власникові векселя суму до 15 бе­резня 2012 року. Власник подав банку вексель достроково — 1 лютого 2012 року, і банк погодився врахувати вексель, але з дисконтом 120%. Скільки одержить влас­ник векселя?

17. Ви можете купити квартиру за 50 тис. дол. готівкою сьогодні або, заплативши 54000 дол. ,через рік, якщо розмі­стите 50 тис. дол. на депозит у банку на рік під 7% річних. Яка альтернатива є переважнішою?

Практичне заняття 3

складні проценти

(Розраховано на 4 год)

План практичного заняття

1. Нарощування за ставкою складних процентів.

2. Дисконтування за ставкою складних процентів.

3. Порівняння інтенсивності процесів нарощування та дисконтування за різними процентними ставками.

Необхідні теоретичні відомості

Для оцінки руху фінансових потоків у часі застосовують різні формули фінансової математики, у тому числі і розрахунок складних процентів. Сутність розрахунку полягає в тому, що проценти, нараховані за період на інвестовані кошти, в наступному періоді приєднаються до основної суми, внаслідок чого в наступному періоді проценти будуть нараховані і на основну суму, і на додані проценти. При цьому відбувається капіталізація процентів у міру їх нарахування, і база, з якою нараховують проценти, постійно зростає.

Наприклад, інвестована 1 грн за ставки 20% дасть 1,20 грн (1 грн інвестовано + 20 коп. процентів); другий рік — 1,44 грн. (до 1 грн інвестицій додають 40 коп. як проценти за основною сумою і 4 коп. як проценти на проценти за перший рік), третій рік — 1,728 грн. (до 1 грн інвестицій додають 60 копійок як проценти за основною сумою і 12,8 коп. як проценти на проценти за два роки) і т. д. У даному прикладі величина 1,20 грн є майбутньою вартістю величини 1 грн, інвестованої строком на 1 рік за процентної ставки 20%.

Формула для розрахунку складних процентів:

FV = PV ∙ (1 + r)ⁿ,

де FV – майбутня вартість; PV – поточна вартість; r – процентна ставка (позиковий відсоток, банківський відсоток); n – кількість років.

Чим довше діє інвестиція і чим вища процентна ставка, тим більша майбутня вартість (рис. 2). Для інвестора за умови нарахування процентів 1 раз на рік вигідніше вкладати гроші за схемою складних процентів, ніж за схемою простих, якщо термін більший 1 року.

Грн

Роки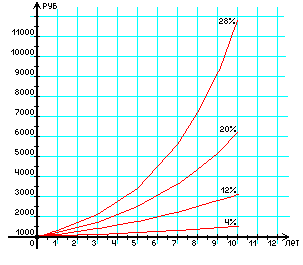

Рис.2. Графік нарахування складних процентів;