Завдання та запитання для самостійної роботи

1. Розкрийте сутність поняття «процент».

2. У чому полягає відмінність між процентом та процентною ставкою?

3. Яким чином встановлюють період нарахування процентів? Як його вимірюють?

4. Розкрийте сутність звичайних (декурсивних) та авансових (облікових) процентів.

5. Що лежить у основі процесу нарощення процентів?

6. Чим прості процентні ставки відрізняються від складних?

7. Визначте порядок розрахунку ставки процента.

8. Розкрийте сутність облікової ставки та порядок її розрахунку.

9. Які особливості застосування на практиці фіксованих та плаваючих ставок?

10. Розкрийте сутність поняття «маржа».

11. Яку ставку вважають базовою (або «прайм рейт»)?

Практичне заняття 2

Прості проценти

(Розраховано на 4 год)

План практичного заняття

1. Нарощення за простою ставкою.

2. Дисконтування за простою ставкою.

Необхідні теоретичні відомості

Під нарощеною сумою позички розуміють початкову суму разом з нарахованими на неї процентами до закінчення строку позички. Процес зміни суми боргу разом з нарахованими процентами за простою ставкою процентів можна записати у вигляді арифметичної прогресії P, P + P · i, P + P · i + P · i і т.д. Перший член дорівнює Р, різниця Рі, останній член являє собою суму боргу S = P + P · i · n.

Сума, накопичена до кінця строку, складається з двох елементів — початкової суми боргу та процентів:

S = P + I,

де І = P · i · n.

Процес нарощення суми боргу за простими процентами являє собою лінійну залежність нарощеної суми S від строку позички (рис. 1).

Очевидно, що сума процентів прямо пропорційно залежить від початкової суми позички, ставки процентів і строку позички. Нарощену суму визначають множенням початкової суми позички на множник нарощення, який показує, у скільки разів нарощена сума більша за початкову. Формула розрахунку множника нарощення залежить від виду застосовуваної процентної ставки та умов нарощення.

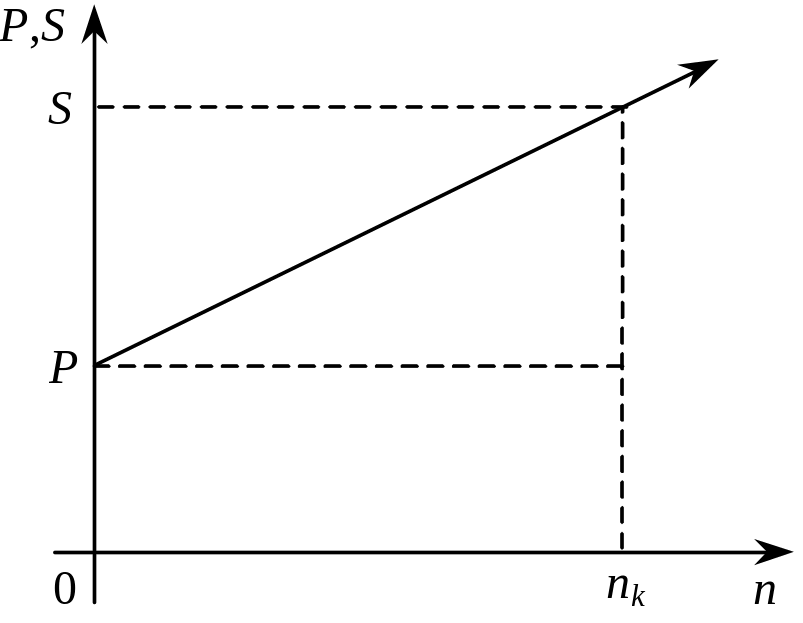
Рис.1. Графік залежності суми боргу від строку позички

За простими процентами

Якщо при цьому використовують просту процентну ставку, то нарощену суму позички визначають за такою формулою:

S = P + I = P (1 + ni).

Величину S називають нарощеною сумою платежу, наведену формулу — формулою нарощення за простими процентами, а множник (1 + ni) — множником нарощення.

Якщо ставка процентів змінюється з часом, то формулу нарощення за простою фіксованою змінною ставкою розраховують таким чином:

,

де i_k — ставка простих процентів для періоду k; n_k — тривалість періоду k.

Як правило, прості проценти застосовують у короткострокових фінансово-кредитних операціях, тобто коли строк позички не перевищує одного року. Оскільки строк позички менший одного року, а процентну ставку встановлюють у розрахунку на один рік, виникає необхідність визначити частину процентів, належну кредитору. Якщо q — кількість днів користування грошима протягом року; К — кількість днів у році (база року), тоді строк користування грошима в роках n можна подати таким чином:

.

Величини q та К можуть набувати різних числових значень. Кількість днів позички (q) обчислюють або точно за календарем, або приблизно, коли вважають, що у місяці 30 днів.

Це стосується також і бази для нарахування процентів, тобто кількості днів у році. Кількість днів у році можна розраховувати точно, за календарем (365 або 366 днів), або приблизно (360 днів). У другому випадку розраховують звичайні або комерційні проценти. Якщо рік визначають за календарем, то обчислюють точні проценти.

Різні значення q та К приводять до різних результатів у нарахуванні простих процентів. Для короткострокових фінансово-кредитних операцій у такому разі застосовують формулу простих процентів:

.

Тут можливі три варіанти розрахунку процентів:

а) звичайні проценти з приблизною кількістю днів позички, коли q має приблизне значення, а К = 360 днів. Такий метод нарахування процентів називають німецькою методикою нарахування процентів. Його застосовують, коли не потрібна велика точність у нарахуванні процентів;

б) комерційні проценти, коли q точне, а К = 360 днів. Цей метод нарахування процентів найчастіше застосовують для обліку векселів та інших операцій у комерційних банках. Цей метод нарахування процентів іноді називають банківським або французьким;

в) точні проценти з точною кількістю днів позички, коли q точ­не, а К = 365 днів. Цей метод дає найточніші результати. На прак­тиці його називають англійським методом нарахування процентів.

Іноді прості проценти можуть використовуватися не лише для короткострокових, а й довгострокових операцій, коли проценти нараховують у споживчому кредиті, як правило, надаваному на кілька років. У такому випадку виникає проблема визначення величини разового погашувального платежу. Його визначають виходячи з суми кредиту і величини нарахованих процентів. Погашення суми кредиту разом з нарахованими процентами відбувається рівними частинами протягом всього строку кредиту. Величину погашувального платежу (q) обчислюють за формулою:

,

де Р — ціна товару або сума кредиту; m — кількість платежів на рік; n — строк кредиту у роках; і — проста річна ставка процентів, під яку надано кредит; q — сума одного платежу для погашення кредиту.

У разі застосування такої методики погашення кредиту фактична сума боргу постійно зменшується, а проценти залишаються сталими протягом усього строку. У даному разі дійсна процентна ставка за споживчим кредитом виявляється більшою, ніж став­ка за умовами кредиту.

Дисконтування та облік за простими процентами

У деяких випадках залежно від умов фінансової угоди необхідно визначати початкову суму боргу за заданою нарощеною сумою боргу S, процентною ставкою і та строком позички n. Проблема полягає в тому, що за відомою сумою S, яку необхідно сплатити через деякий час n, необхідно визначити суму отриманої позички Р. Операцію такого характеру у фінансових розрахунках називають дисконтуванням, а різницю між нарощеною сумою S і початковою величиною Р — дисконтом.

Якщо проценти утримуються безпосередньо під час видачі позички, тоді застосовують облікову ставку. У разі використання облікової ставки для видачі позички головним завданням є визначення початкової суми боргу (Р) або суми на будь-яку дату до моменту сплати нарощеної суми (S).

У такому разі вважають, що сума дисконтується, а різницю S – P = D називають дисконтом.

Необхідність визначення P за S виникає також під час купівлі банком векселів.

Існує два види дисконтування:

1) математичне дисконтування;

2) банківський облік.

До математичного дисконтування вдаються в тих випадках, коли за заданими S, n та i необхідно знайти Р:

,

де — дисконтний множник.

Величину Р, якщо її знайдено за S, називають дисконтованою величиною S, або сучасною величиною платежу S, або теперішньою вартістю.

Банківський, або комерційний, облік полягає в тому, що банк до кінцевої дати платежу за векселем або іншим короткостроковим зобов’язанням купує його у власника і бере на себе весь ризик з отримання грошей. При цьому ціна, за якою банк купує вексель, повинна бути менша за ціну, вказану на векселі. Таким чином банк, продавши його векселедавцю, отримає дохід, реалізуючи тим самим дисконт.

Необхідність визначення дисконту виникає для різних фінансових операцій, зокрема обліку векселів та інших короткострокових зобов’язань. У такому разі звичайно застосовують не математичний, а банківський облік. Згідно з цим методом проценти за користування позичкою розраховують із суми, яку необхідно виплатити в кінці строку позички. Ставку, за якою нараховані проценти, називають обліковою або дисконтною (d). Річні облікові ставки розраховують за такою формулою: тоді як звідси P = S (1 – nd).

Дисконт P = S – D = S – Sdn = S (1 – nd).

Величину (1 – nd) називають дисконтним множником, який показує, у скільки разів початкова величина Р менша за нарощену величину S.

Дисконтування за обліковою ставкою здійснюють, як правило, за умови, що рік дорівнює 360 днів, а кількість днів у періоді приблизна, тобто місяць дорівнює 30 дням, незалежно від кількості днів у місяці за календарем.

Необхідно враховувати таку властивість простих облікових ставок: якщо n > 1/d, величина Р буде від’ємна.

Якщо необхідно на основі облікової ставки визначити суму, яку потрібно поставити в бланку векселя, тоді на основі початкової величини та облікової ставки визначають нарощену суму.

Формула нарощення за обліковою ставкою має такий вигляд:

де коефіцієнт 1/(1 – nd) - множник нарощення, в основу якого покладена облікова ставка.

Еквівалентність ставки процентів і облікової ставки систематизовані нижче.

Показник	Ставка процентів	Облікова ставка
Нарощення	S = P (1 + ni)
Визначення початкової суми		P = S (1 – nd)
Процент, дисконт	Ii = S – P = Pni	Dd = S – P = Snd

Часто в процесі укладання кредитних угод виникає необхідність визначення строку, на який може бути надана позичка, якщо відома початкова величина, сума, яку необхідно погасити в кінці строку, та рівні процентної ставки.

Строк позички і рівень процентних ставок визначають за такими формулами: