Сведение многокритериальной задачи к однокритериальной

Рассмотрим подробнее формальную постановку метода сведения многокритериальной задачи к однокритериальной. В случаях, когда информированность ЛПР о целях выбора является достаточно полной для введения метрики в критериальное пространство, в качестве критериальной постановки можно использовать обобщенный (интегральный) критерий q₀(x), выражаемый целевой функцией. Введем интегральный критерий q₀(x) как скалярную функцию векторного аргумента:

q₀(x)= f((q₁(x), q₂(x),…, q_n(x)). (9.1)

Интегральный критерий позволяет упорядочить альтернативы по величине q₀, выделив тем самым наилучшую (в смысле этого критерия). Вид функции q₀ определяется тем, как конкретно представляется вклад каждого критерия в интегральный критерий. Обычно используют аддитивные и мультипликативные функции:

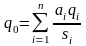^{при ai > 0; (9.2)}

^{при bi > 0, (9.2)}

где a_i – весовой коэффициенты соответствующих показателей критерия;

s_i – нормирующий коэффициент.

Коэффициент a_i отражают относительный вклад частных критериев q_i в интегральный критерий. А коэффициент s_i обеспечивают:

• безразмерность числа a_iq_i/s_i (различные частные критерии могут иметь разную размерность, и тогда над ними нельзя производить арифметических операций и свести их в интегральный критерий);

• нормировку, т.е. обеспечение условия a_iq_i/s_i<1;

• сохранение целевой функции в диапазоне от 0 до 1, для чего сумма s_i должна равняться 1.

Итак, в многокритериальной постановке задача принятия решения о выборе одной из альтернатив сводится к максимизации интегрального критерия:

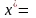
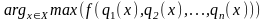. (9.3)

Основная проблема в многокритериальной постановке задачи принятия решений состоит в том, что необходимо найти такой аналитический вид коэффициентов a_i, который бы обеспечил следующие свойства модели:

• высокую степень адекватности в предметной области с точки зрения экспертов;

• минимальные вычислительные трудности максимизации интегрального критерия, т.е. его расчета для разных альтернатив;

• устойчивость результатов максимизации интегрального критерия от малых возмущений исходных данных.

Последнее означает, что малое изменение исходных данных должно приводить к малому изменению величины интегрального критерия и соответственно к малому изменению принимаемого решения. Таким образом, если исходные данные практически те же, то и решение должно приниматься или то же самое, или очень близкое.

Для оценки весовых коэффициентов наибольшее распространение получил метод экспертных оценок, среди которых по распространенности выделяются:

1. Метод предпочтения. В этом методе каждый эксперт должен проранжировать показатели качества так, чтобы на первое место поставить наименее важный показатель качества, на второе – следующий за ним и т. д. Весовой коэффициент i-го фактора рассчитывается по формуле

^,

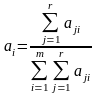где r – количество экспертов;

m – количество показателей качества;

а_ji – место, на которое поставлена весомость i-го фактора у j-го эксперта.

Это достаточно грубый метод, предполагающий равные градации по шкале относительной важности.

2. Метод ранга. Предполагает, что эксперт должен оценивать важность каждого фактора по шкале относительной значимости в диапазоне от 1 до 10. Разрешается выбирать и дробные значения. Весовые коэффициенты определяются по формуле

^{при , (9.6)}

где r_ji – оценка значимости i-го фактора у j-гo эксперта.

3. Метод последовательных сопоставлений. Этот метод основан на следующей процедуре оценки важности критериев. Эксперт ранжирует критерии в порядке предпочтения. Для наиболее важного показателя назначается a₁ = l, а для остальных показателей из {q} – значения, взятые в интервале a_i = [0, 1] в соответствии с их приоритетами. Далее ЛПР решает, будет ли коэффициент a₁ = l у первого по важности критерия q₁ превосходить все остальные вместе взятые коэффициенты a₂ + а₃ + ... + a_m или необходимо увеличить значение а₁ так, чтобы оно становилось больше, чем сумма всех последующих

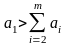, (9.7)

В противном случае изменяется величина а₁ так, чтобы выполнялось условие

. ^(9.8)

На следующих шагах эксперт повторяет эту процедуру со всеми оставшимися m – 1 показателями качества. По совокупности экспертов обработка результатов производится по формулам метода ранга (9.5).