Кодирование звуковой информации

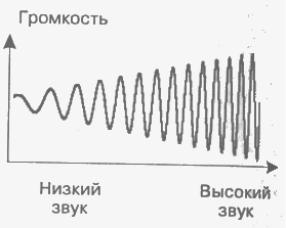
Звуковой сигнал - это непрерывная волна с изменяющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче звук, чем больше частота сигнала, тем выше тон.

Для того чтобы компьютер мог обрабатывать непрерывный звуковой сигнал, он должен быть преобразован в цифровую дискретную форму с помощью временной дискретизации.

Ч астота дискретизации звука – это количество измерений звука за одну секунду. Чем больше количество измерений производится за 1 секунду, тем качественнее звук.

Глубина кодирования звука (I)– это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.

Количество уровней громкости рассчитывается по формуле N =2^I=2¹⁶=65536

Информационный объем цифрового стерео звукового файла длительностью звучания 1 секунда при среднем качестве звука (16 битов, 24 КГц) будет равен:

16 бит 24000  2 = 768 000 бит=96 000 байт=93,75 Кбайт

Количество выборок в секунду может быть в диапазоне от 8000 до 48000, т.е. частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 Кгц.

Кодирование числовой информации

Система счисления – совокупность правил наименования и изображения чисел с помощью набора символов (цифр).

Цифры – это символы, через которые выражается число.

Число – это количественное выражение.

Системы счисления	Позиционные системы счисления – количественное значение символа зависит от его места (позиции) в числе.	Непозиционные системы счисления - количественное значение символа определяется только изображением и не зависит от его места (позиции) в числе.
Пример	Десятичная, (15, 51) восьмеричная, шестнадцатеричная, двоичная.	Римская система (VI, IV) I(1); V(5); X(10); L(50); C(100); D(500); M(1000).
Свойства	представляются дробные и отрицательные числа, действия над числами имеют правила.	не представляются дробные и отрицательные числа, действия над числами не имеют правил, используются для обозначения томов, дат, глав книг.

Запись числа 1998 в римской системе счисления

MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1

Развернутая запись числа в десятичной системе счисления

1978₍₁₀₎= 8 * 10 ⁰+ 7 * 10 ¹ + 9 * 10 ² + 1 *10 ³

3 2 1 0 – разряд

Основание системы равно количеству цифр (символов в ее алфавите), определяет, во сколько раз различаются значения цифр соседних разрядов.

Позиционные системы счисления

Система счисления	используемые цифры	основание
Десятичная	0 1 2 3 4 5 6 7 8 9	10
Двоичная	0 1	2
Восьмеричная	0 1 2 3 4 5 6 7	8
Шестнадцатеричная	0 1 2 3 4 5 6 7 8 9 A(10) B(11) C(12) D(13) E(14) F(15)	16

Перевод целых чисел из двоичной в десятичную систему счисления

101₍₂₎= 1 х 2 ⁰ + 0 х 2 ¹ + 1 х 2 ² = 5

^{2 1 0}

десятичная	1	2	3	4	5	6	7	8	9	10
двоичная	1	10	11	100	101	110	111	1000	1001	1010