Контрольні питання та завдання:
Які методи використовує SADT-аналітик для вивчення предметної області?
Що є джерелами інформації?
Як проводити процес опитування? Що потрібно пам’ятати при опитуванні?
З чого починається моделювання SADT?
Що означає декомпозиція діаграми?
Лекція 17. Тема: побудова sadt-діаграм
17.1 Побудова SADT-діаграми для процесу "Скласти навчальний розклад"
Опишемо весь процес моделювання, використовуючи SADT-методологію, на прикладі процесу "скласти навчальний розклад".
Нагадаємо про допущення зроблені в цьому завданні. Для простоти завдання вважатимемо, що в нашому випадку завжди є вільні викладачі, вільні аудиторії.
Спершу складемо список даних і список функцій, які є в даному процесі (рис17.1).
Список даних |
Список функций |
|
|
Рисунок 17.1 – Організувати процес “Скласти розклад занять”
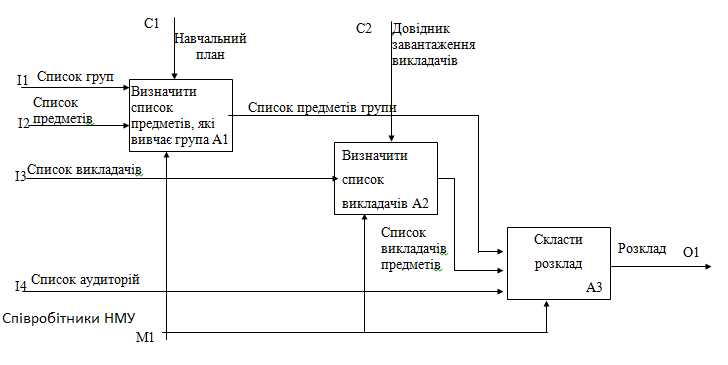
Рисунок 17.2 – Діаграма А0
Р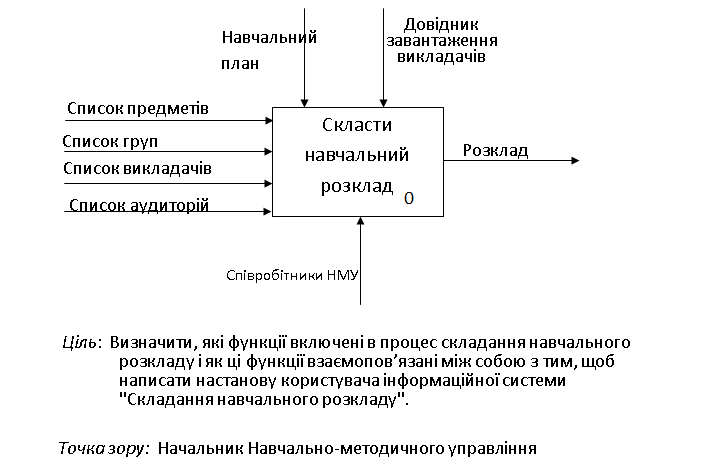
исунок
17.3 – Діаграма А-О
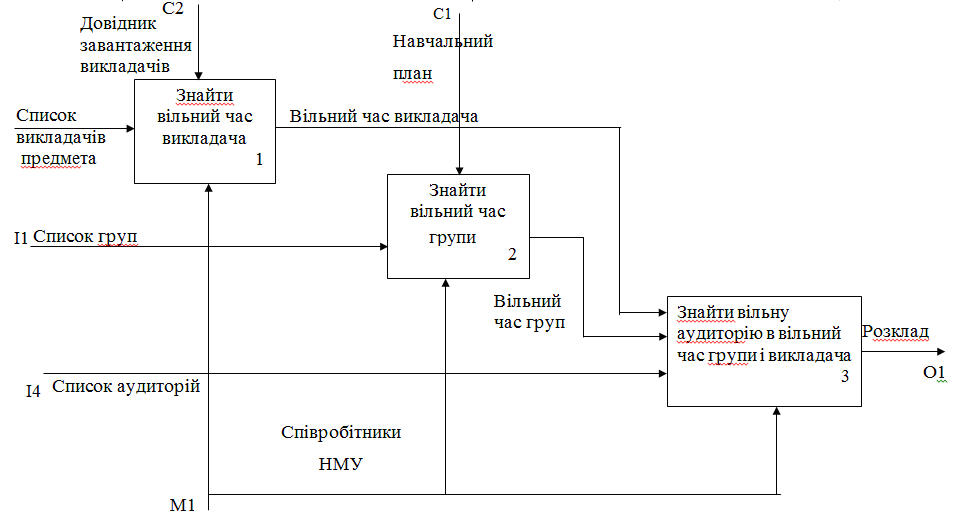
Рисунок 17.4 – Декомпозиція блоку А3
17.2. Побудова sadt-діаграми для процесу “Побудова таблиць/графіків функцій однієї змінної”
Розробимо функціональну діаграму на прикладі уточнення специфікацій програми побудови таблиць/графіків функцій однієї змінної. Діаграма, показана на рис. 17.5, а, є діаграмою верхнього рівня. На ній добре видно, що є початковими даними для програми, і яких результатів роботи від неї чекають.
Діаграма, представлена на рис. 17.5, б, уточнює функції програми. На ній показані чотири блоки: Введення/вибір функцій і її розбір, Додавання функції в список, Побудову таблиці значень і Побудова графіка функції. Для кожного блоку визначені початкові дані, керуючі дії і результати. Згідно правилам найменування входів/виходів, що мають продовження на батьківській діаграмі, на діаграмі використані наступні позначення:
I1 - функція
I2 - відрізок
I3 – крок
С1 - вигляд графік/таблиця
О1 - графік функції на відрізку
О2 - таблиця значень функції на відрізку.
С
ловник
в цьому випадку повинен містити опис
всіх даних, що використовуються в
системі.
Функціональну модель доцільно застосовувати для визначення специфікацій програмного забезпечення, що не передбачає роботу з складними структурами даних оскільки вона орієнтована на декомпозицію функцій. SADT-модель – це ще не специфікація. Вона містить добре організовану і точну сукупність інформації, за допомогою якої можна створити специфікацію.
Типи зв'язків між функціями
На SADT-діаграмах явно не вказані ні послідовність, ні час. Проте, зворотні зв'язки, ітерації, процеси, що продовжуються, і функції, що перекриваються (за часом), можуть бути зображені за допомогою дуг. Розрізняють сім типів зв’язування.
Тип випадкового зв'язування
Зв'язок між функціями малий або повністю відсутній.
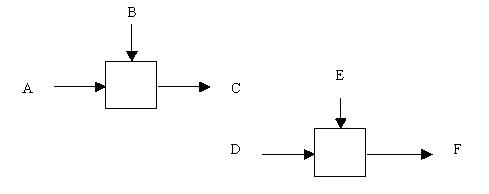Рисунок
17.6 – Випадкове зв’язування
Тип логічного зв'язування.
Дані і функції потрапляють в загальний клас або набір елементів, але функціональних відносин між ними немає.
Тип тимчасового зв'язування.
Функції зв’язані в часі, коли їх дані використовуються одночасно або функції включаються паралельно, а не послідовно.
Тип процедурного зв'язування.
Функції виконуються протягом однієї і тієї ж частини циклу або процесу (рис.17.7).
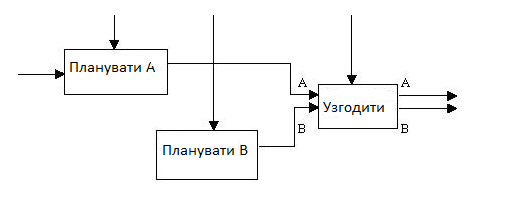Рисунок
17.7 - Процедурне зв’язування
Тип комунікаційного зв'язування.
Блоки використовують одні і ті ж вхідні дані і/або проводять одні і ті ж вихідні дані (рис.17.8).
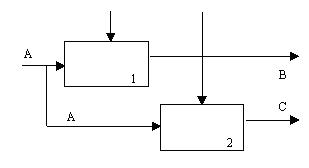Рисунок
17.8 – Комунікаційне зв’язування
Тип послідовного зв'язування.
Вихід однієї функції служить вхідними даними для наступної функції. Моделює причинно-наслідкові залежності (рис.17.9).
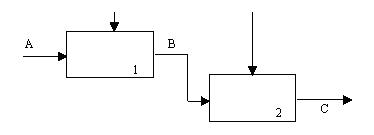Рисунок
17.9 – Послідовне зв’язування
Тип функціонального зв'язування.
Відображає наявність повної залежності однієї функції від іншої. (рис.17.10).
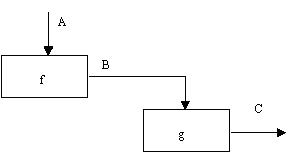Рисунок
17.10 – Функціональне зв’язування
Функціональний зв'язок, показаний на рисунку, в математичних термінах може мати вигляд: C = g(B)= g(f(A)).