3. Геометрическое распределение

Геометрическое распределение (Фарри). Это закон распределения дискретной случайной величины, связанный с последовательностью независимых испытаний, при этом случайной величиной является число проведённых испытаний до первого осуществления наблюдаемого события.

Например

• число выстрелов до первого попадания в цель;

• число проверенных изделий до первого появления бракованного изделия;

• число подбрасываний кубика до выпадения шести очков и т.п.

Если случайная величина Х имеет геометрическое распределение, то она будет принимать значения k - натуральные числа 1, 2, 3,…, счетное число значений, и p это вероятность наступления события в одном испытании, то вероятность

₍₁₄₎

Замечание: при любом значении p, не равном нулю или единице, наивероятнейшим значением является единица. C ростом k вероятности монотонно убывают.

Вероятности 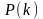для последовательных значений k образуют геометрическую прогрессию с первым членом р и знаменателем (1-p), откуда и название «геометрическое распределение».

Основные числовые характеристики геометрического распределения:

1. Математическое ожидание

₍₁₅₎

2. Дисперсия

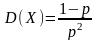₍₁₆₎

Пример 5: Кубик подбрасывается до тех пор, пока не выпадет 6 очков. Найти вероятность, что выпадение 6 очков случится за 5 бросков.

Решение:

Для первого броска (k = 1), вероятность успеха p(1) = 1/6.

Для второго (k = 2) это вероятность успеха во втором броске и неудачи в первом по формуле (14):

для третьего броска:

для четвертого броска:

для пятого броска:

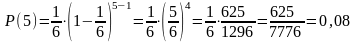
Ответ: вероятность, что выпадение 6 очков случится за 5 бросков равна 0,08.

Пример 6: Ролик кодового замка содержит 7 возможных цифр, из которых нужно выбрать одну. Какова вероятность, что его можно открыть точно с 3-го раза.

Решение:

Вероятность правильного единичного выбора

Распределение геометрическое значит искомую вероятность найдем по формуле (14)

Если замок состоит из нескольких независимых роликов, то вероятность его случайного открывания подчиняется уже другому распределению – биномиальному.

Ответ: вероятность, что замок откроется точно с 3-го раза равна 0,105.

Пример 7: Контроль качества партии продукции проводится до обнаружения первого бракованного изделия. В результате серии проверок обнаружили, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить вероятность появления брака.

Решение:

Пусть Х – число испытаний до первого появления бракованного изделия. Х случайная величина имеет геометрическое распределение. По условию ее среднее значение равно

Так как , то _.

Ответ: вероятность появления брака равна 0,1.

4. Гипергеометрическое распределение

Гипергеометрическое распределение имеют случайные величины, которые имеют место при выборочном контроле некоторой совокупности N объектов по некоторому определенному свойству. Для каждого рассматриваемого объекта дают ответ на вопрос - обладает он свойством А, или нет. Гипергеометрическое распределение имеет случайная величина Х, равная числу объектов, обладающих свойством А в случайной выборке объема n, где n<N.

Например:

• число некачественных единиц изделий в случайной совокупности объема n из партии объема N, если n<N;

• лотерея, в которой свойство А билета – это «быть выигрышным», тогда всего билетов N, а некоторое лицо приобрело n из них, в этом случае число выигрышных билетов у этого лица имеет гипергеометрическое распределение.

Таким образом, гипергеометрическое распределение - дискретная случайная величина Х состоящая в том, что в выборке из N объектов, из которых т обладают свойством А, будет именно k, обладающих свойством А, в выборке из п конкретных объектов взятых из совокупности.

₍₁₇₎

При этом т объектов обладают свойством А, k – объектов попало в выборку, всего попало в выборку п элементов из N.

Таким образом, гипергеометрическое распределение определяется тремя параметрами – объемом генеральной совокупности N, числом объектов т в ней, обладающих рассматриваемым свойством А, и объемом выборки n.

Основные числовые характеристики гипергеометрического распределения: