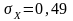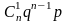6. Примеры законов распределения дискретных случайных величин

1. Биномиальное распределение

Рассмотрим осуществление схемы Бернулли, т.е. прозводится серия повторных независимых испытаний, в каждом из которых данное событие А имеет одну и ту же вероятность 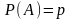, не зависящую от номера испытания. И для каждого испытания имеются только два исхода:

1. событие А – успех;

2. событие 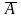- неуспех,

с постоянными вероятностями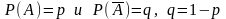

Введем в рассмотрение дискретную случайную величину Х – «число появлений события А при п испытаниях» и найдем закон распределения этой случайной величины. Величина Х может принимать значения

Вероятность того, что случайную величину Х примет значение x_k находится по формуле Бернулли

(1)

Закон распределения дискретной случайной величины, определяемый формулой Бернулли (1), называется биномиальным законом распределения. Постоянные п и р (q=1-p), входящие в формулу (1) называются параметрами биномиального распределения.

Название «биномиальное распределение» связано с тем, что правая часть в равенстве (1) это общий член разложения бинома Ньютона ,т.е.

(2)

А так как p+q=1, то правая часть равенства (2) равна 1

(3)

Это означает, что

(4)

В равенстве (3) первый член qⁿ в правой части означает вероятность того, что в п испытаниях событие А не появится ни разу, второй член 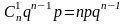вероятность того, что событие А появится один раз, третий член – вероятность, что событие А появится два раза и наконец, последний член р^п – вероятность того, что событие А появится ровно п раз.

Биномиальный закон распределения дискретной случайной величины представляют в виде таблицы:

Х	0	1	…	k	…	n
Р	qn		…		…	рп

Основные числовые характеристики биномиального распределения:

1. математическое ожидание (5)

2. дисперсия 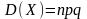(6)

3. среднее квадратическое отклонение (7)

4. наивероятнейшее число появление события k₀ – это число которому при заданном п соответствует максимальная биномиальная вероятность

При заданных п и р это число определяется неравенствами

(8)

если число пр+р не является целым, то k₀ равно целой части этого числа, если же пр+р – целое число, то k₀ имеет два значения

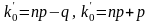
Биномиальный закон распределения вероятностей применяется в теории стрельбы, в теории и практике статистического контроля качества продукции, в теории массового обслуживания, в теории надежности и т.д. Этот закон может применяться во всех случаях, когда имеет место последовательность независимых испытаний.

Пример 1: Проверкой качества установлено, что из каждых 100 приборов не имеют дефекты 90 штук в среднем. Составить биномиальный закон распределения вероятностей числа качественных приборов из приобретенных наугад 4.

Решение: Событие А – появление которого проверяется это – «приобретенный наугад прибор качественный». По условию задачи основные параметры биномиального распределения:

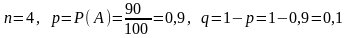
Случайная величина Х – число качественных приборов из взятых 4, значит значения Х - Найдем вероятности значений Х по формуле (1):

Таким образом, закон распределения величины Х - число качественных приборов из взятых 4:

Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561

Для проверки правильности построения распределения проверим чему равна сумма вероятностей

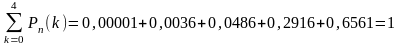
Ответ: Закон распределения

Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561

Пример 2: Применяемый метод лечения приводит к выздоровлению в 95 % случаев. Пятеро больных применяли данный метод. Найти наивероятнейшее число выздоровевших, а так же числовые характеристики случайной величины Х – число выздоровевших из 5 больных применявших данный метод.

Решение: Событие А - больной применявший лечение выздоровел, тогда основные параметры биномиального распределения:

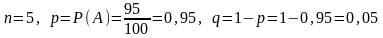
По формуле (8) найдем 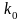наивероятнейшее число выздоровевших из 5. Найдем 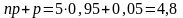получили не целое число значит равно целой части, т.е. .

Теперь найдем числовые характеристики Х – число выздоровевших из 5 больных применявших данный метод лечения:

1. математическое ожидание по формуле (5)

2. дисперсия по формуле (6)

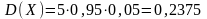
3. среднее квадратическое отклонение по формуле (7)

Ответ: