
- •Оглавление
- •Предисловие
- •1. Методические рекомендации
- •1.1. Рекомендации по выполнению заданий
- •1.2. Рекомендации по написанию реферата
- •1.3. Рекомендации по подготовке доклада для конференции
- •2. Тематика исследовательских работ
- •Тема 1. Простые и составные числа
- •Литература:
- •Тема 2. Простые числа «близнецы»
- •Литература:
- •Тема 3. Проблема Гольдбаха
- •Литература:
- •Тема 4. Совершенные числа
- •Литература:
- •Тема 5. Приветливые, дружественные и общительные числа
- •Литература:
- •Тема 6. Магические квадраты
- •Литература:
- •Дополнительная литература:
- •Тема 7. Полумагический числовой коврик
- •Литература:
- •Тема 8. Магические треугольники
- •Литература:
- •Тема 9. Магические квадраты из простых чисел
- •Литература:
- •Тема 10. Задача Пуассона
- •Литература:
- •Тема 11. Лабиринты
- •Литература:
- •Тема 12. Окружность и круг
- •Литература:
- •Тема 13. Принцип Дирихле3
- •Литература:
- •Тема 14. Положительные и отрицательные целые числа
- •Литература:
- •Целочисленные прямоугольные треугольники
- •Введение
- •Часть 1. Основные понятия, используемые в работе
- •1.1. Понятие прямоугольного треугольника
- •1.2. Теорема Пифагора
- •1.3. Понятие целочисленного прямоугольного треугольника
- •Часть 2. Постановка и решение задач исследования
- •2.1. Постановка первой задачи
- •2.2. Постановка второй задачи
- •2.3. Теорема о примитивной пифагоровой тройке
- •Заключение
- •Литература:
- •Темы исследовательских работ по математике для учащихся 5-6 классов
Литература:
1.Баврин И.И., Фрибус Е.А. Старинные задачи: Кн. для учащихся. –М.: Просвещение, 1994. С. 36, 86-87.
2. Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред. шк. –М.: Просвещение, 1989. С.265-267.
3.Задачи для внеклассной работы по математике в 5-6 классах: Пособие для учителей /Сост. В.Ю. Сафонова; Под ред. Д.Б. Фукса, А.Л. Гавронского.- М.: МИРОС, 1993.- С.29-30.
4. Оре О. Приглашение в теорию чисел: Пер. с анг. –М.: Наука. Гл. ред. ф.-м. лит-ры, 1980. (Б-чка «Квант». Вып. 3).С.15- 22.
Дополнительная литература:
1.Берколайко С.Т. Условия существования магических квадратов 3х3 и их свойства // Математика в школе. 1992. №4-5.С. 33-35.
2. Гуревич Е.Я. Тайна древнего талисмана. М.: Наука, 1969.
3. Постников И.М. Магические квадраты. – М.: Наука, 1964.
Тема 7. Полумагический числовой коврик
Так условно называют числовой квадрат 9х9, который предлагает искусно «соткать» из девяти девятиклеточных квадратов Ф.Ф. Егоров [1].
Задание:
№1. «Соткать» полумагический коврик с учетом следующих требований:
В каждом из девяти одинаковых девятиклеточных квадратов требуется ( в разных вариантах) разместить все натуральные числа от 1 до 9 и затем соединить все девять квадратов в один квадратный числовой коврик размером 9х9.
Числа должны быть размещены так, чтобы:
1) сумма чисел по каждой диагонали в любом девятиклеточном варианте равнялась 15;
2) сумма чисел в каждом из четырех квадратов 2х2, входящих в состав девятиклеточного квадрата, а также сумма чисел, расположенных в клетках, прилегающих к сторонам центрального квадратика, равнялась 16 в первом девятиклеточном квадрате коврика, 17 во втором, 18 –в третьем и далее последовательно 19, 20, 21, 22, 23, 24. Например, в таблицах 1 и 2 каждая из пяти сумм
|
1 |
9 |
2 |
||||||
|---|---|---|---|---|---|---|---|---|---|
|
5 |
6 |
4 |
||||||
|
7 |
3 |
8 |
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
3 |
4 |
2 |
8 |
7 |
9 |
6 |
1 |
5 |
3) в каждом столбце и каждой строке полного «сотканного» квадрата 9х9 содержались бы все числа от 1 до 9 в произвольной последовательности.
№2. Придумай алгоритм составления требуемого числового квадрата 9х9.
№3. Выяви как можно больше интересных числовых свойств у образовавшегося квадрата.
После выполнения всех заданий напиши реферат по теме «Полумагический числовой коврик».
Литература:
1.Кордемский Б.А. «Полумагический» числовой коврик // Математика в школе. 1977. №3. С. 84.
Тема 8. Магические треугольники
Если девять первых натуральных чисел расположить в форме треугольника так, чтобы вдоль каждой из сторон была одна и та же сумма, то такой треугольник называют магическим (Рис. 1).
Рис. 1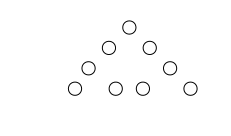 З
З
№1. Найди хотя бы один такой треугольник.
№2. Найди всевозможные магические треугольники с суммой 17. Опиши, как ты их нашел.
№3. Найди всевозможные магические треугольники с суммой 19. Опиши, как ты их нашел.
№4. Найди всевозможные магические треугольники с суммой 20. Опиши, как ты их нашел.
№5. Найди всевозможные магические треугольники с суммой 21. Опиши, как ты их нашел.
№6. Найди всевозможные магические треугольники с суммой 23. Опиши, как ты их нашел.
№7. Доказать, что не могут быть треугольники с другим значением суммы, кроме указанных в № 2- 6.
№8. Можно ли придумать какой-нибудь способ составления магического треугольника
После выполнения всех заданий напиши реферат по теме «Магические треугольники»
