3.2Двоичная арифметика

Двоичная система счисления является минимальной системой, в которой реализуется принцип позиционности в цифровой форме записи числа. В двоичной системе счисления значение каждой цифры по месту при переходе от любого данного разряда к следующему старшему разряду увеличивается вдвое.

Утверждение двоичной арифметики в качестве общепринятой основы при конструировании ЭВМ с программным управлением состоялось под влиянием работы А. Беркса, Х. Гольдстайна и Дж. фон Неймана над проектом первой ЭВМ с хранимой в памяти программой.

Арифметика двоичной системы счисления, как и всякой другой позиционной системы, основывается на использовании таблиц сложения и умножения цифр.

X	0	1
0	0	0
1	0	1

+	0	1
0	0	1
1	0	10

Сложение двух многозначных двоичных чисел проводится «столбиком». Выравниваем два числа по запятой, а затем складываем соответствующие разряды этих чисел. При сложении двух единиц в соответствующем разряде суммы записываем ноль и единицу переносим в соседний старший разряд. Например:

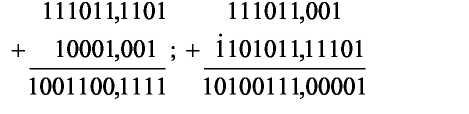
3.3Компьютерное представление чисел

Для представления чисел в компьютере используется две формы:

с фиксированной запятой

с плавающей запятой

Первая форма применятся для целых чисел, которые могут быть как со знаком (+/-), так и без знака. Формат записи целых чисел без знака:

Однобайтовый формат записи числа 73.

27	26	25	24	23	22	21	20	Веса разрядов
1	0	0	0	1	1	1	0
7	6	5	4	3	2	1	0	Номера разрядов

Количество чисел, которое можно записать в одном байте – 2⁸-1 = 255. Двухбайтовый формат:

215	214	213	212	211	210	29	28	27	26	25	24	23	22	21	20	Веса разрядов
0	0	0	0	0	0	0	0	1	0	0	0	1	1	1	0
15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0	Номера разрядов

Количество чисел, которое можно записать в двух байтах – 2¹⁶-1 = 65535.

При представлении целых числа со знаком старший (крайний слева) разряд отображает знак числа и называется знаковым, остальные разряды являются числовыми и образуют поле числа. Если число положительное, то знаковый разряд равен 0. Если отрицательное, то единице.

Пример записи числа со знаком:

А = 11011₂, В = -1011

Знак	26	25	24	23	22	21	20	Веса разрядов
0	0	0	1	1	0	1	1
7	6	5	4	3	2	1	0	Номера разрядов

Знак	26	25	24	23	22	21	20	Веса разрядов
1	0	0	0	1	0	1	1
7	6	5	4	3	2	1	0	Номера разрядов

Форма с плавающей запятой используется для представления вещественных чисел и соответствует экспоненциальной записи числа в математике. Например, 0,00256=2,5610^-3=0,25610^-2. Чтобы исключить неоднозначность записи значение мантиссы должно удовлетворять следующему неравенству 0,1 |М| 1.

Пример записи двоичного числа 0,11001012^-10

Знак числа	Знак порядка	24	23	22	21	20	2-1	2-2	2-3	2-4	2-5	2-6	2-7	2-8	2-9	Веса разрядов
0	1	0	0	0	1	0	1	1	0	0	1	0	1	0	0
15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0	Номера разрядов
	Поле порядка						Поле мантиссы

Запись чисел с плавающей запятой позволяет записать большее количество чисел по сравнению с записью с фиксированной запятой. Однако устройства, которые реализуют вычисления с числами в этом представлении значительно сложнее и обладают меньшим быстродействием.