2.7. Застосування методу Ньютона для знаходження

екстремальних точок функції

Задачу обчислення значень аргументу функції , за яких функція досягає своїх екстремальних значень (максимального чи мінімального), можна звести до задачі розв’язання нелінійних рівнянь, оскільки в даних точках похідна від функції дорівнює нулю, тобто . При цьому ітераційна формула набуває вигляду:

, (2.23)

Приклад 7. Користуючись методом Ньютона знайти координати екстремальної точки функції , яка знаходяться на відрізках .

Лістинг обчислення координати екстремальної точки та значення екстремуму, реалізованого в пакеті Mathcad, наведено на рис. 12. На цьому ж лістингу наведено результат, одержаний за допомогою вбудованої процедури root.

Рис. 12.

2.8. Метод хорд

Нехай потрібно розв’язати рівняння (2.1), яке має єдиний корінь на інтервалі , для якого виконується умова (рис. 13). Для побудови ітераційної формули методу хорд запишемо рівняння прямої (хорди), яка проходить через дві точки і :

Поклавши в одержаному рівнянні , дістанемо формулу для обчислення наближень за методом хорд вигляду:

, (2.24)

де – нерухома точка.

Рис. 14

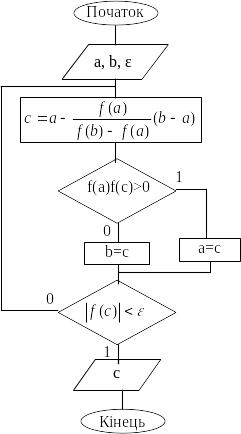
Рис. 13

Можна показати, що за нерухому точку береться той із кінців відрізка , для якого виконується умова . Інший кінець інтервалу приймається за початкове наближення . Ітераційний процес закінчується в разі виконання умови

, де , тому що існує оцінка . Блок-схема алгоритму показана на рис. 14.

2.9. Комбінований метод

О

Рис. 15

скільки в методах хорд і дотичних наближення кореня обчислюється відповідно з недостачею і з надлишком (залежно від вигляду кривої), то був розроблений метод, який об’єднав обидва підходи (рис.15). Процес закінчується, коли

.

Кінцеве наближення обчис­лю­­ється за формулою

,

де і – наближення кореня, отримані методами Ньютона та хорд.

Приклад 8. Користуючись методами хорд та комбінованим знайти корені рівняння .

Лістинги обчислення коренів указаними вище методами наведено, відповідно, на рис. 16, 17.

Зауважимо, що при знаходженні кореня рівняння, який знаходиться на відрізку за нерухому точку в комбінованому методі потрібно брати лівий кінець відрізка, тобто , а за початкове наближення правий кінець відрізка, тобто точку .

Рис. 16

Рис. 17

2.10. Застосування засобів пакету Mathcad для знаходження

коренів алгебраїчних рівнянь

Корені алгебраїчного рівняння, яке має дійсні або комплексні корені

(2.25)

можна знайти за допомогою вбудованої процедури polyroоts, яка має вигляд:

polyroоts(V),

де V – вектор з коефіцієнтів многочлена вигляду (Т – операція транспонування).

Приклад 9. На лістингу (рис. 18), наведеному приклади застосування процедури polyroоts для знаходження коренів рівнянь у випадку простих та кратних коренів. З наведених прикладів бачимо, що дана процедура, у випадку кратних коренів, може працювати не зовсім надійно (випадки 2, 3). Тому, при одержанні коренів потрібно виконувати їх перевірку.

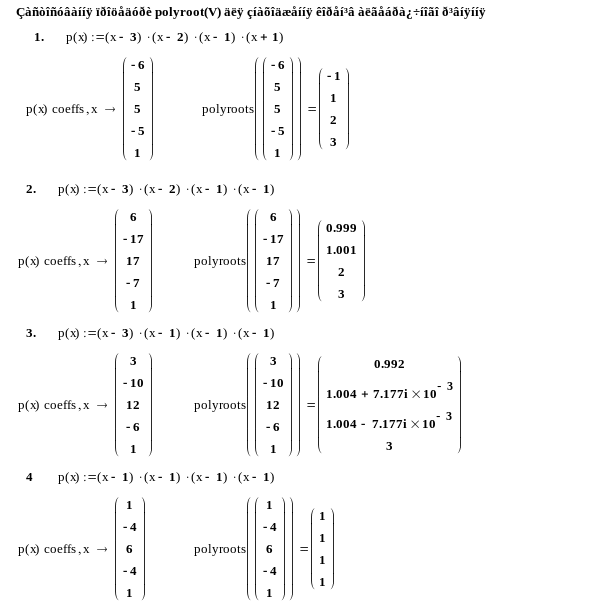
Рис. 18

15