2.5. Метод Ньютона

Для прискорення збіжності ітераційного процесу методу простої ітерації (2.6) функцію можна вибрати у вигляді

.

У цьому випадку чергове наближення буде знаходитись за формулою

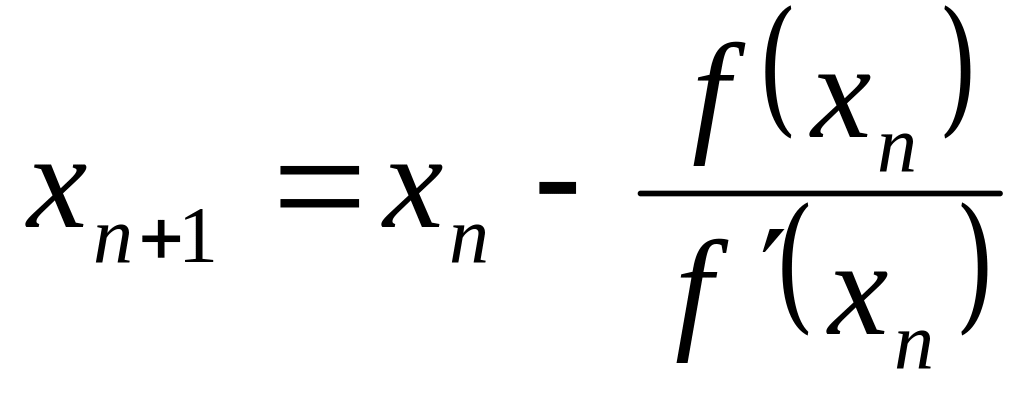, (2.17)

Формулу (2.17) можна отримати з рівняння дотичної до графіка функції в точці , де – -е наближення до кореня рівняння (рис.9).

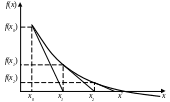
Рис. 9.

Як відомо, рівняння дотичної має вигляд

,

де – довільна точка на дотичній. Поклавши в рівнянні дотичної (точка перетину дотичної з віссю ОХ) дістанемо формулу (2.17).

Достатні умови збіжності методу Ньютона дає така теорема.

Теорема. Нехай на відрізку функція має неперервні із сталими знаками похідні , і . Тоді існує такий окіл кореня рівняння , що для будь-якого послідовність , обчислена за формулою (2.17), збігається до кореня .

Доведення. Для доведення збіжності послідовність до кореня досить показати, що похідна задовольняє умов для будь-якого , і взяття з околу кореня .

Для похідної маємо вираз

.

Оскільки неперервна і відмінна від нуля на , то існують такі додатні і , що і для будь-якого значення .

Тоді .

З неперервності функції випливає, що існує окіл кореня , на якому функція задовольняє нерівність , внаслідок чого, для будь-якого . А це і є достатня умова збіжності ітераційного процесу. Теорему доведено.

Припустивши, що в околі кореня і неважко одержати оцінку швидкості збіжності обчислень за формулою (2.17). Для чого в околі кореня рівняння розкладемо функцію в ряд Тейлора з урахуванням третього члена, що визначає нелінійність апроксимації:

, . (2.18)

Врахувавши, що рівність (2.18) можна перетворити до вигляду (з врахуванням (2.17)):

.

Оскільки і , то з умови, що , одержуємо квадратичну залежність похибки на послідовних ітераціях:

, де . (2.19)

Таким чином метод Ньютона має квадратичну збіжність

, , (2.20)

де .

Приклад 5. Користуючись методом Ньютона для простих коренів уточнити корінь рівняння , який знаходиться на відрізку .

Лістинг відокремлення кореня та обчислення його методом Ньютона, реалізованого в пакеті Mathcad, наведено на рис. 10.

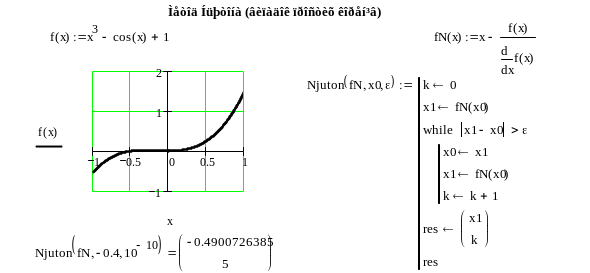
Рис. 10.

2.6. Метод Ньютона для кратних коренів

Швидкість збіжності методу Ньютона падає, якщо рівняння має кратні корені. Разом з тим квадратичну збіжність можна зберегти, якщо побудувати дещо іншу ітераційну формулу, яка базується на наступному відомому факті. Якщо функція має деякий корінь кратності , то її похідна має цей самий корінь кратності .

У більшості випадків кратність коренів невідома, тому для збереження квадратичної збіжності на базі заданого рівняння з кратним коренем розглядають рівняння

, (2.21)

яке має корінь кратності одиниця, незалежно від його кратності у вихідному рівнянні .

Як відомо, для рівняння ітераційний процес має вигляд

,

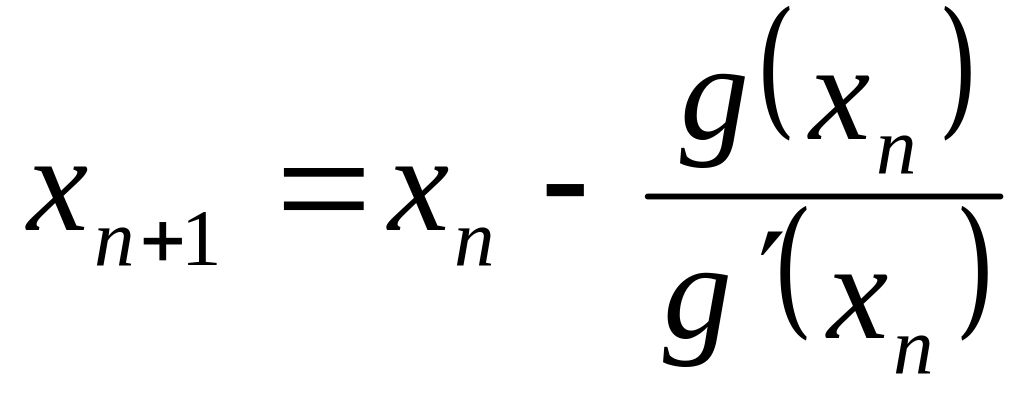Оскільки , то .

Враховуючи одержану рівність дістанемо формулу методу Ньютона для кратних коренів, яка має вигляд

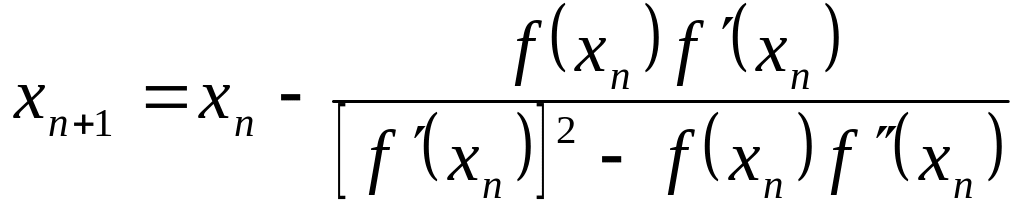, (2.22)

Приклад 6. Користуючись методом Ньютона для кратних коренів уточнити корінь рівняння , який знаходиться на відрізку . Неважко переконатись, що це є корінь , який має кратність два.

Лістинг відокремлення кореня та обчислення його методом Ньютона, реалізованого в пакеті Mathcad, наведено на рис. 11.

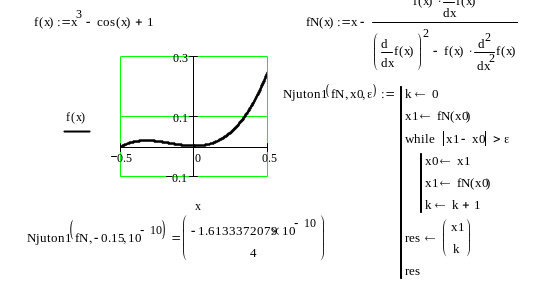
Рис. 11.