2.3. Метод поділу відрізку навпіл

Метод поділу відрізку навпіл (дихотомії) передбачає послідовне обчислення значень функції в ряді точок. Перед використанням методу необхідно визначити відрізок, який містить лише один корінь рівняння. Для пошуку такого відрізку можна скористатись графічним способом.

Нехай потрібно знайти корінь рівняння (2.1), який знаходиться на відрізку . У випадку єдиного кореня на вказаному відрізку буде виконуватись умова

. (2.2)

Далі відрізок починають зменшувати, визначаючи на кожному кроці алгоритму координати його нових граничних точок і за значеннями , та координати середини відрізка :

.

У залежності від знаку функції в точці новий відрізок знаходження кореня встановлюється за допомогою наступного правила:

(2.3)

де ; – середня точка відрізку (рис.3). Блок-схема алгоритму поділу відрізка навпіл наведено на рис. 4

Рис. 3

Рис. 4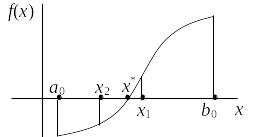

Довжина відрізка ізоляції кореня після виконання кроків зменшується до величини

,

а значення кореня , обумовлено координатою середньої точки, і його похибки задаються виразами:

. (2.4)

Із формули (2.4) випливає, що збіжність процесу обчислень дуже повільна, оскільки точність в одному десятковому розряді досягається за 3-4 кроки через те, що . Разом з тим, цей метод має абсолютну збіжність, тому ніяких вимог до вигляду і властивостей функції не висувається.

Приклад 2. Користуючись методом поділу відрізка навпіл обчислити корені рівняння із заданою точністю та підрахунком числа ітерацій.

Лістинг обчислення кореня рівняння, який знаходиться на відрізку методом поділу відрізка навпіл, реалізованого в пакеті Mathcad, наведено на рис. 5.

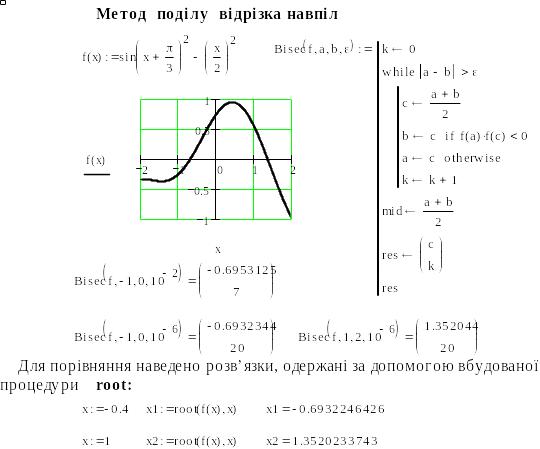
Рис. 5.

Таким чином: при значення кореня , число ітерацій ; при значення кореня , число ітерацій ;

2.4. Метод простої ітерації

Метод простої ітерації полягає в тому, що рівняння (2.1) записують у канонічному вигляді:

, (2.5)

а ітерації здійснюються за правилом

, (2.6)

де початкове наближення задається з відрізка , який містить корінь рівняння.

Якщо процес обчислень збігається до розв’язу рівняння (2.5), тобто , то припустивши, що функція визначена, неперервна і диференційована на відрізку, який містить шуканий корінь, можна встановити умову збіжності ітераційного процесу (зв’язок між похибками обчислень на двох сусідніх ітераціях):

, . (2.7)

Із рівності (2.7) випливає достатня умова збіжності методу простої ітерації, а саме, буде менше за умови

. (2.8)

Якщо покласти , то достатня умова збіжності методу простої ітерації має вигляд . Чим менше значення , тим швидше збігається ітераційний процес.

У випадку, коли в околі кореня похідна задовольняє умову похибки і будуть мати однакові знаки і збіжність до буде монотонною (рис.6, а). Якщо ж виконується умова – , похибки і матимуть різні знаки і наближення буде збігатися до , коливаючись біля (рис.6, б).

У випадку, коли , похибка за абсолютним значенням буде більшою за , і наближення буде знаходитись далі від розв’язку ніж , тобто процес буде розбіжний (рис.6, в, г).

Рис. 6. Можливі варіанти збіжності ітерацій: а) – монотонна збіжність;

б) – коливальна збіжність; в) – монотонна розбіжність; г) – коливальна розбіжність.

Зауважимо, що коли , то збіжність ітерацій замість лінійної, обумовленої виразом (2.7), стає нелінійною, зокрема квадратичною. Це має місце в методі Ньютона, який розглянемо пізніше.

Оцінювання глобальної похибки зручно виконувати на основі значень локальної похибки, тобто за значеннями наближень, отриманих на сусдніх ітераціях за аналогією з формулою (2.7). Для цього формулу (2.7) запишемо у вигляді:

,

або

.

Звідки отримуємо оцінку

, (2.9)

де .

Якщо обчислення починати від початкового значення , то для поточної похибки на -й ітерації згідно з формулами (2.7) і (2.9) можна одержати оцінку

. (2.10)

Приклад 3. Користуючись методом ітерацій уточнити корінь рівняння , який знаходиться на відрізку .

Лістинг відокремлення кореня та обчислення його методом ітерацій, реалізованого в пакеті Mathcad, наведено на рис. 7.

Рис. 7

Якщо покласти , , то оцінку (2.10) можна записати у вигляді

, (2.11)

Якщо похибка обчислення кореня рівняння не повинна перевищувати наперед заданого значення , то згідно з формулою (2.11) можна знайти необхідну кількість ітерацій

(2.12)

У тих випадках, коли не вдається явно розв’язати вихідне рівняння відносно невідомої , так щоб у рівнянні (2.5) функція задовольняла умову збіжності (2.8), ітерації можна виконувати за правилом:

(2.13)

Тут допоміжна функція не повинна змінювати свій знак на відрізку, де шукають корінь. Зокрема, якщо , одержимо метод релаксації:

(2.14)

для якого і умова збіжності має вигляд

, (2.15)

Якщо в деякому околі кореня виконуються умови

, ,

то метод релаксації збігається в разі . Оптимальне значення параметра в такому випадку має вигляд

. (2.16)

Приклад 4. Користуючись модифікованим методом ітерацій уточнити корінь рівняння , який знаходиться на відрізку .

Лістинг відокремлення кореня та обчислення його методом ітерацій, реалізованого в пакеті Mathcad, наведено на рис. 8.

Рис. 8.