Комп’ютерні системи та мережі

Розділ 2. Чисельні методи розв’язання нелінійних рівнянь

2.1. Постановка задачі

Нехай потрібно розв’язати нелінійне рівняння

, (2.1)

де функція визначена і неперервна на деякому проміжку . Якщо функція — алгебраїчний многочлен, то рівняння (2.1) називається алгебраїчним. Якщо функція містить тригонометричні, показникові або логарифмічні функції, тоді рівняння (2.1) називають трансцендентним.

Розв’язати рівняння означає знайти множину його коренів, тобто таких значень , при яких рівняння (2.1) перетвориться в тотожність. Корінь рівняння (2.1) ще називається нулем функції .

Знайти точні значення коренів заданого рівняння можна лише для найпростіших функцій : алгебраїчних многочленів не вище четвертого степеня, деяких многочленів степеня і деяких трансцендентних функцій.

Універсальних методів для знаходження точних значень коренів алгебраїчних рівнянь степеня і трансцендентних рівнянь не існує. Тому розв’язання нелінійних рівнянь виконується переважно чисельними методами, які базуються на ітераційності розв’язку і локальності апроксимації.

Нехай – точний корінь, а ­– його наближене значення. Кажуть, що корінь обчислено з наперед заданою точністю , якщо . Нехай, наприклад, і , тоді числа і — наближені значення кореня відповідно з недостачею і надлишком з точністю . У цьому випадку за наближене значення з точністю можна взяти будь-яке число з відрізка .

У загальному випадку процедура розв’язання нелінійних рівнянь складається з двох етапів:

• відокремлення коренів рівняння, тобто попереднє знаходження інтервалів, що містять лише один корінь (локалізація коренів);

• уточнення коренів, тобто обчислення коренів із заданою точністю.

Перший етап називають ще задачею визначення відрізків ізоляції коренів, а другий – уточненням наближених коренів. Перший етап, як правило, складніший за другий, оскільки для загального випадку немає досить ефективних методів відокремлення коренів. Для знаходження коренів з наперед заданою точністю застосовують методи, які дають можливість уточнювати знайдені наближення коренів. Такі методи називаються ітераційними.

2.2. Відокремлення коренів

Перший етап (відокремлення коренів) здійснюється, як правило, графічно. Для цього будується графік функції . Точки перетину графіка з віссю ОХ і є коренями рівняння. Часто рівняння (2,1) записують у вигляді і будують графіки функцій і потім знаходять межі, в яких містяться абсциси точок перетину графіків функцій і .

Інколи для відокремлення коренів можна скористатись табличним методом. Він полягає в знаходженні послідовності значень функції з певним кроком і виявлені зміни знака в значення членів послідовності. Для цього, за допомогою дискретної змінної, будують вектор із значень функції, який дає можливість побачити зміни знака функції, що свідчить про наявність коренів.

Приклад 1. Відокремити корені рівняння користуючись двома варіантами графічного та табличного методів.

Лістинг двох варіантів графічного метод відокремлення коренів, реалізований в пакеті Mathcad, наведено на рис. 1, табличного методу на (рис. 2).

Рис. 2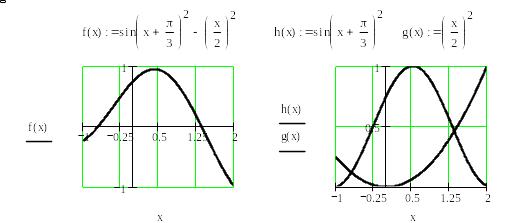

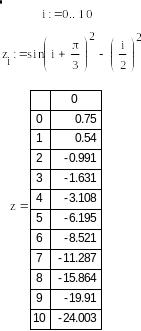
Рис. 1

Другий етап починається з вибору початкової точки (початкового наближення кореня) і обчислюється нев’язка . Якщо або достатньо близьке до нуля, то корінь знайдено. В іншому випадку, за певним алгоритмом, формується послідовність наближень з використанням інформації про знак нев’язки, про значення самої нев’язки тощо.

Вибір початкового значення є важливим етапом, який істотно впливає на ефективність процедури розв’язання і навіть на можливість одержання розв’язку.