5. Метод Ньютона для кратних коренів

Швидкість збіжності методу Ньютона падає, якщо рівняння має кратні корені. Разом з тим квадратичну збіжність можна зберегти, якщо побудувати дещо іншу ітераційну формулу, яка базується на наступному відомому факті. Якщо функція має деякий корінь кратності , то її похідна має цей самий корінь кратності .

У більшості випадків кратність коренів невідома, тому для збереження квадратичної збіжності на базі заданого рівняння з кратним коренем розглядають рівняння

, (21)

яке має корінь кратності одиниця, незалежно від його кратності у вихідному рівнянні .

Як відомо, для рівняння ітераційний процес має вигляд

,

Знайшовши похідну і підставивши її в останню дістанемо формулу методу Ньютона для кратних коренів, яка має вигляд

, (22)

Приклад 6. Користуючись методом Ньютона для кратних коренів уточнити кратний корінь рівняння , який знаходиться на відрізку . Неважко переконатись, що це є корінь , який має кратність два.

Лістинг з відокремленням кореня та обчислення його методом Ньютона для кратних коренів, реалізованого в пакеті Mathcad, наведено на рис. 7. Для порівняння на (рис. 8) наведено Лістинг уточнення кореня медом Ньютона для простих коренів. Різниця в кількості ітерацій значна – 4 і 25 відповідно.

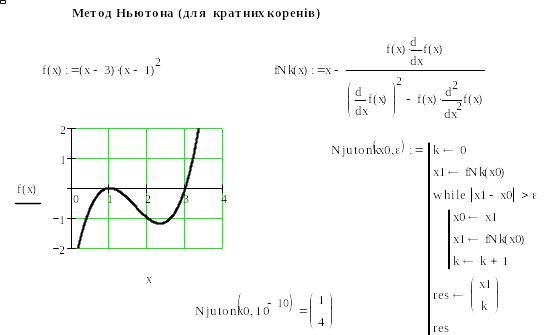
Рис.7.

Рис.8.

6. Застосування методу Ньютона для знаходження

екстремальних точок функції

Задачу обчислення значень аргументу функції , за яких функція досягає своїх екстремальних значень (максимального чи мінімального), можна звести до задачі розв’язання нелінійних рівнянь, оскільки в даних точках похідна від функції дорівнює нулю, тобто . При цьому ітераційна формула набуває вигляду:

, (23)

Приклад 7. Користуючись методом Ньютона знайти координати екстремальної точки функції , яка знаходяться на відрізках .

Лістинг обчислення координати екстремальної точки та значення екстремуму, реалізованого в пакеті Mathcad, наведено на рис. 9. На цьому ж лістингу наведено результат, одержаний за допомогою вбудованої процедури root.

Рис. 9.

7. Метод хорд

Нехай потрібно розв’язати рівняння (1), яке має єдиний корінь на інтервалі , для якого виконується умова . Для побудови ітераційної формули методу хорд запишемо рівняння прямої (хорди), яка проходить через дві точки і :

Поклавши в одержаному рівнянні , дістанемо формулу для обчислення наближень вигляду:

, (24)

де – нерухома точка.

М ожна показати, що за нерухому точку береться той із кінців відрізка , для якого виконується умова . Інший кінець інтервалу приймається за початкове наближення (рис. 10). Ітераційний процес закінчується в разі виконання умови

,

де , тому що існує оцінка

Рис. 10

.

1.9. Комбінований метод

Оскільки в методах хорд і дотичних наближення кореня обчислюється відповідно з недостачею і з надлишком (залежно від вигляду кривої) був розроблений метод, який об’єднав обидва підходи (рис.11). Процес закінчується, коли

.

Кінцеве наближення обчислюється за формулою

,

де і – наближення кореня, отримані методами Ньютона та хорд.

Рис. 11.