Задача 2

Исследовать динамику экономического показателя на основе анализа одномерного временного ряда

В течение девяти последовательных недель фиксировался спрос на кредитные ресурсы финансовой компании. Временной ряд этого показателя приведен в Таблице 9.

Таблица 9

№ наблюдения	Y(t), млн.руб.
1	20
2	27
3	30
4	41
5	45
6	51
7	51
8	55
9	61

1. Проверить наличие аномальных наблюдений.

2. Построить линейную модель Y(t)=a0+a1t, параметры которой оценить при помощи МНК (Y(t) – расчетные, смоделированные значения временного ряда).

3. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7 ÷ 3,7).

4. Оценить точность модели на основе использования средней относительной ошибки аппроксимации.

5. Осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности p=70%).

6. Фактические значения показателя, результаты моделирования представить графически.

Вычисления провести с тремя знаками в дробной части. Основные промежуточные результаты вычислений привести в таблицах. При использовании компьютера представить соответствующие листинги с комментариями.

1. Корреляционное поле представлено на Рис.3. Визуально - аномальных наблюдений не отмечено.

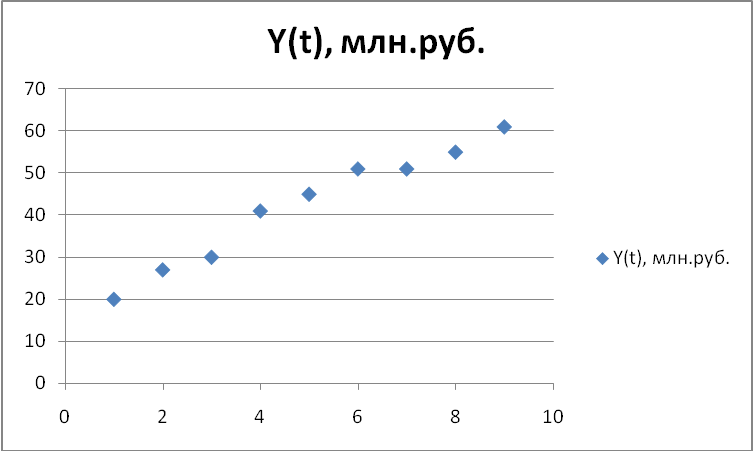
Рис.3

Проверим наличие аномальности наблюдений по методу Ирвина. Рассчитаем значения λ, Sy и сравним данные с табличными.

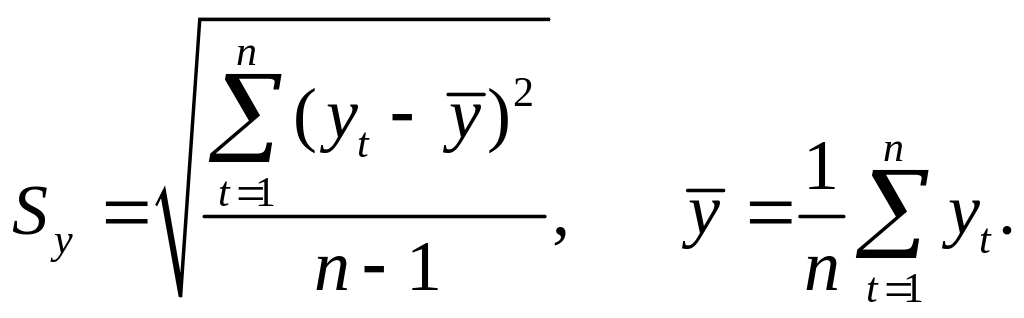
Результаты расчета приведены в таблице 9.

	№ наблюдения	Y(t), млн.руб.	λ	Y-Yср	(Y-Yср)^2
	1	20		-22,333	498,778
	2	27	0,502	-15,333	235,111
	3	30	0,215	-12,333	152,111
	4	41	0,789	-1,333	1,778
	5	45	0,287	2,667	7,111
	6	51	0,430	8,667	75,111
	7	51	0,000	8,667	75,111
	8	55	0,287	12,667	160,444
	9	61	0,430	18,667	348,444
Сумма	45	381			1554,000
Среднее		42,333
Sy		13,937

Сравним значения с табличными для количества наблюдений – 10.

Критические значения параметра . (Таблица 10).

Количество наблюдений n
	P=0,95	P=0,99
2	2,8	3,7
3	2,2	2,9
10	1,5	2,0
20	1,3	1,8

Произведенные расчеты доказывают отсутствие аномальности.

2. Линейная модель Y(t)=a0+a1t построена при помощи функции «регрессия» пакета анализа MS Excel. Параметры модели определены МНК.

Уравнение приняло следующий вид: Y = 17,333+5*t

Проведем анализ статистической значимости параметров модели.

Рассчитаем стандартную ошибку оценки остатков Se и среднеквадратические отклонения коэффициентов регрессии Sα и Sβ - стандартные ошибки(отклонения) по ниже приведенным формулам:

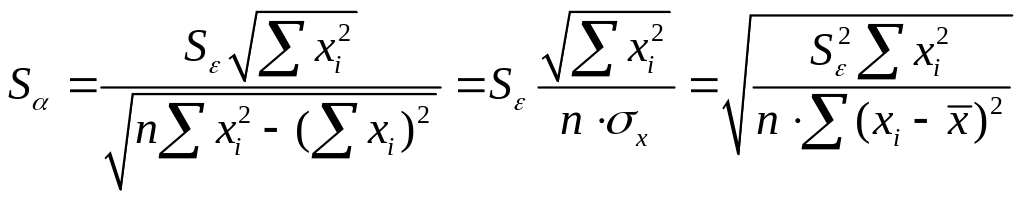
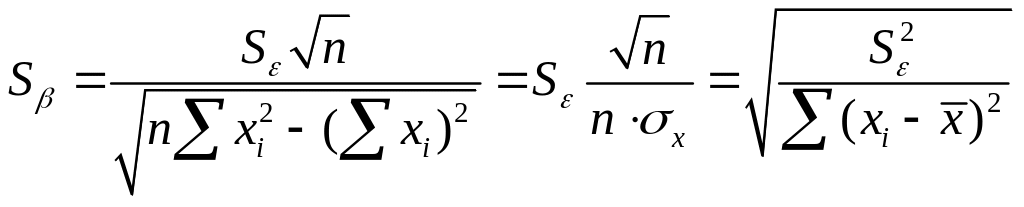
Проверку значимости коэффициентов регрессии определим рассчитав значения t-критерия (t–статистики) для соответствующих коэффициентов регрессии:

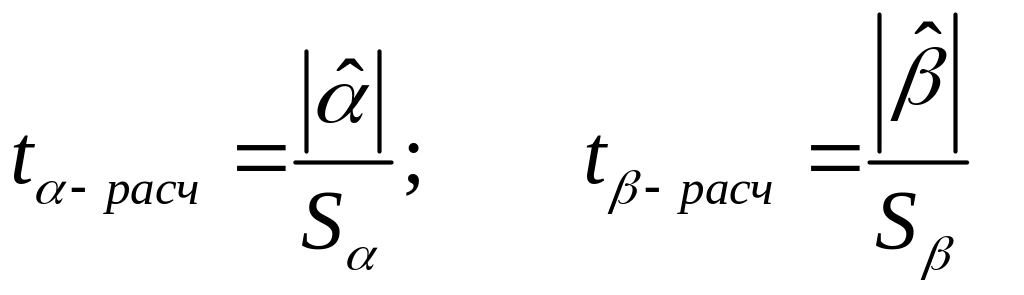
Результаты расчетов сведены в таблицу 11:

Стандартная ошибка оценки	Se	2,777
Стандартная ошибка отклонения	Sα	2,018
Стандартная ошибка отклонения	Sβ	0,359
Расчетные значения t-критерия	Tα	8,590	tα табл	2,365
Расчетные значения t-критерия	Tβ	13,944	tβ табл	2,365

Сравним расчетные значения с табличными t_табл. Табличное значение критерия определяется при (n-2) степенях свободы (n - число наблюдений) и соответствующем уровне значимости  ( 0,05)

Расчетные значение t-критерия с (n - 2) степенями сво­боды превосходит его табличное значение при заданном уровне зна­чимости, таким образом коэффициент регрессии модели являются значимыми.

3. Оценка адекватности построенной модели

   1. Используя свойства независимости остаточной компоненты с помощью d-критерия Дарбина-Уотсона. Рассчитаем d-критерий по формуле:

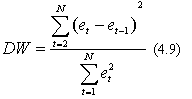
Приближенная формула: DW=2(1-r)

Первый коэффициент корреляции остатков рассчитаем по формуле:

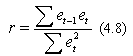
Расчетные значения приведены в Таблице 12:

Критерий Дарбина Уотсона	DW	1,352
Критерий Дарбина Уотсона(вычислено через R(1))	DW	1,486
Табличное значение	DW low	0,820
Табличное значение	DW up	1,320

Рассчитаем шкалу Дарбина Уотсона.

Шкала Дарбина-Уотсона

0,000

0,820

1,320

2

2,680

3,180

Ниже приведено расчетное значение Первого коэффициента автокорреляции.

Коэффициент автокорреляции

r(1)

0,257

tβ табл

2,262

Расчетное значение DW, приближенного и точного попадает в интервал – отсутствие автокорреляции.

По данному критерию модель адекватна, значение DW говорит об отсутствии автокорреляции в остатах.

2. Проверка условия случайности

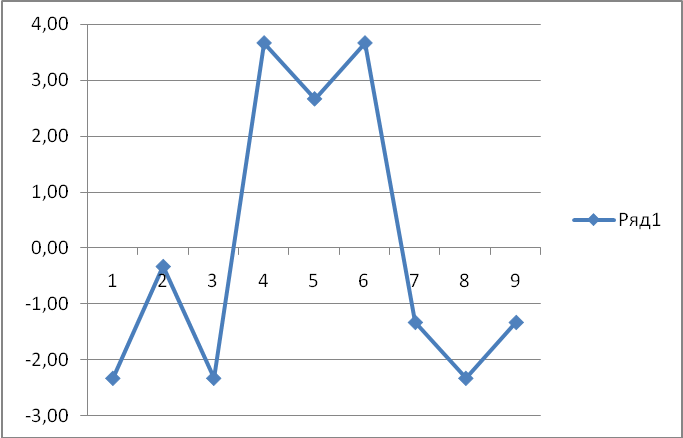
Рис. 4. График остатков

Критерий случайности отклонений от тренда при уровне вероятности 0,95 можно представить как

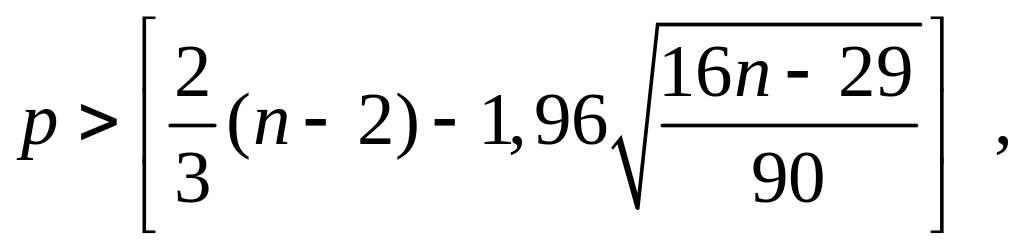
где р – фактическое количество поворотных точек в случайном ряду.

Количество поворотных точек	p	6,00
Критерий случайности отклонения от тренда при уровне вероятности 0,95%	p расч	2,45

Неравенство 6>2,45 выполняется, модель по критерию случайности адекватна.

3. Проверка нормальности распределения остаточной компоненты при помощи RS- критерия

.

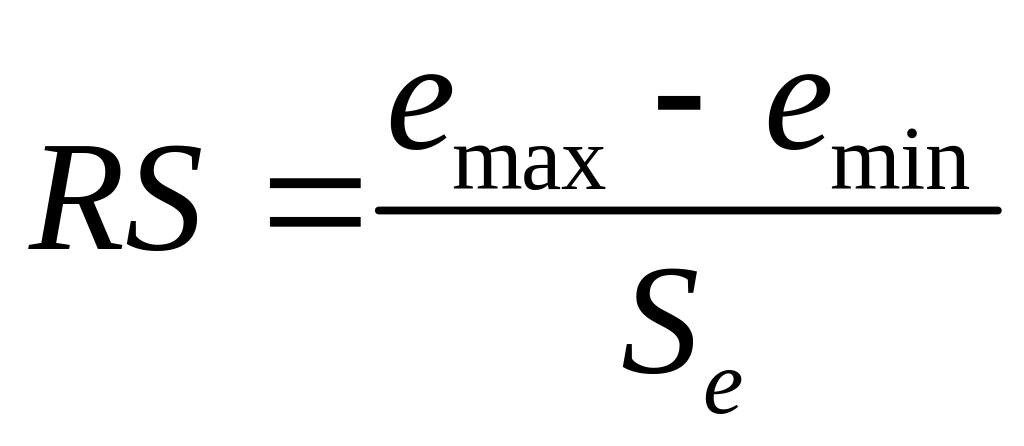где – максимальный уровень ряда остатков,

– минимальный уровень ряда остатков,

– среднеквадратическое отклонение.

Emax	3,667
Emin	-2,333
RS	2,160

Расчетное значение попадает в интервал (2,7 – 3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна.

4. Рассчитаем среднюю относительную ошибку аппроксимации по нижеприведенной формуле:

Чем меньше рассеяние эмпирических точек вокруг теоре­тической линии регрессии, тем меньше средняя ошиб­ка аппроксимации. Ошибка аппроксимации меньше 7 % свидетельствует о хорошем качестве модели.

Результаты расчета приведены в таблице.

Средняя относительная ошибка аппроксимации

A

5,75%

Расчеты показывают, что качество и точность модели модели высокие.

Все промежуточные расчеты представлены в Таблице 13:

№ наблюдения	Y(t), млн.руб.	Предсказанное Y(t), млн.руб.	E(t)	E(t)^2	E(t)/Yi	t2	E(t-1)	E(t)*E(t-1)	(E(t)-(E(t-1))^2
1	20	22,33	-2,33	5,44	0,12	1,00
2	27	27,33	-0,33	0,11	0,01	4,00	-2,33	0,778	4,000
3	30	32,33	-2,33	5,44	0,08	9,00	-0,33	0,778	4,000
4	41	37,33	3,67	13,44	0,09	16,00	-2,33	-8,556	36,000
5	45	42,33	2,67	7,11	0,06	25,00	3,67	9,778	1,000
6	51	47,33	3,67	13,44	0,07	36,00	2,67	9,778	1,000
7	51	52,33	-1,33	1,78	0,03	49,00	3,67	-4,889	25,000
8	55	57,33	-2,33	5,44	0,04	64,00	-1,33	3,111	1,000
9	61	62,33	-1,33	1,78	0,02	81,00	-2,33	3,111	1,000
45	381	381	0,00	54,00		285,00		13,889	73,000