9. Первая космическая скорость

А 1

Какое выражение определяет значение скорости движения по круговой орбите спутника планеты массой , если радиус планеты , а расстояние от поверхности планеты до спутника ?

1) 2)

3) 4)

А 2

Космический корабль движется вокруг Земли по круговой орбите радиусом 20000 км. Масса Земли . Определите скорость корабля.

1) 4,5 км/с 2) 6,3 км/с

3) 8 км/с 4) 11 км/с

С 1

Каков радиус кольца Сатурна, в котором частицы движутся со скоростью 10 км/с? Масса Сатурна равна кг.

С 2

Среднее расстояние от планеты Земля до Солнца составляет 149,6 млн. км, а от планеты Юпитер до Солнца – 778,3 млн. км. Чему равно отношение линейных скоростей двух планет при их движении вокруг Солнца, если считать их орбиты окружностями? (2,3)

С 3

Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн. км, а до планеты Земля - 149,6 млн. км. Какова приблизительно средняя линейная скорость планеты Уран при ее движении вокруг Солнца, если известно, что средняя скорость движе­ния Земли по орбите вокруг Солнца составляет 30 км/с? (6,84 км/с)

С 4

На сколько процентов отличаются скорости двух частиц, входящих в состав колец Сатурна, если они вращаются независимо по круго­вым орбитам с радиусами 120 000 км и 380 000 км? (На 43,8 %, если за 100 % брать скорость на ближайшей к Сатурну орбите или на 78%, если за 100 % брать скорость на дальней орбите)

А 3

Средняя плотность планеты Плюк равна средней плотности планеты Земля, а радиус Плюка в 2 раза больше радиуса Земли. Определите отношение первой космической скорости на Плюке к первой космической скорости на Земле .

1) 1 2) 2

3) 1,41 4) 4

А 4

Плотность Меркурия примерно равна плотности Земли, а радиус в 2,63 раза меньше. Определите отношение первой космической скорости на Меркурии к первой космической скорости на Земле .

1) 0,38 2) 1,62

3) 2,63 4) 6,92

А 5

Искусственный спутник обращается по круговой орбите на высоте 600 км от поверхности планеты. Радиус планеты равен 3400 км, ускорение свободного падения на поверхности планеты равно 4 м/с². Какова скорость движения спутника по орбите?

1) 3,4 км/с 2) 3,7 км/с

3) 5,4 км/с 4) 6,8 км/с

А 6

Искусственный спутник обращается по круговой орбите на высоте 600 км от поверхности планеты со скоростью 3,4 км/с. Радиус планеты равен 3400 км. Чему равно ускорение свободного падения на поверхности планеты?

1) 3 км/с² 2) 4 м/с²

3) 9,8 м/с² 4) 9,8 км/с²

А 1

Период обращения и радиус орбиты Фобоса, одного из спутников Марса, были измерены астрономами и оказались примерно равными соответственно 7,6 ч и 9400 км. Гравитационная постоянная, измеренная Г. Кавендишем на Земле, равна примерно . Можно ли вычислить на основании этих данных массу Марса?

1) Нет, так как константы, измеренные на Земле, нельзя использовать для расчетов параметров других планет.

2) Нет, так как масса – экспериментально измеряемая, а не вычисляемая теоретически величина.

3) Да, на основании 2-ого закона Ньютона и закона всемирного тяготения она может быть оценена в 6,5 ∙ 10²³ кг.

4) Да, на основании законов Ньютона ее масса примерно равна массе Земли 6 ∙ 10²⁴кг.

С 1

Масса Марса составляет 0,1 от массы Земли, диаметр Марса вдвое меньше, чем диаметр Земли. Каково отношение периодов обращения искусственных спутников Марса и Земли, двигающихся по круговым орбитам на небольшой высоте? (1,1)

С 2

Масса планеты составляет 0,2 от массы Земли, диаметр планеты втрое меньше, чем диаметр Земли. Чему равно отношение периодов обращения искусственных спутников планеты и Земли , двигающихся по круговым орбитам на небольшой высоте? (0,43)

С 3

Средний радиус Марса примерно в 2 раза меньше среднего радиуса Земли, а его масса примерно в 10 раз меньше. Во сколько раз при- мерно отличаются периоды обращения искусственного спутника вблизи поверхности Земли и Марса? (0,9)

С 4

Среднее расстояние от Солнца до планеты Уран составляет 2875,03 млн. км, а до планеты Земля - 149,6 млн. км. Чему пример­но равен период обращения Урана (в годах) вокруг Солнца, если орбиты обеих планет считать окружностями? (84,24 года)

С 5

Каков радиус кольца Сатурна, в котором частицы движутся с пе­риодом примерно равным периоду вращения Сатурна вокруг своей оси 10 час. 40 мин.? Масса Сатурна равна кг.

С 6

С какой скоростью движутся частицы, входящие в наиболее плот­ное кольцо Сатурна, если известно, что их период примерно совпа­дает с периодом вращения Сатурна вокруг своей оси 10 час. 40 мин.? Масса Сатурна равна кг. (18416 м/с)

А 2

Плотность Меркурия приблизительно равна плотности Земли, а масса в 18 раз меньше. Определите отношение периода обращения спутника, движущегося вокруг Меркурия по низкой круговой орбите, к периоду обращения аналогичного спутника Земли.

1) 1 2) 2

3) 1,41 4) 2,82

А 3

Плотность Марса приблизительно равна плотности Земли, а масса в 10 раз меньше. Определите отношение периода обращения спутника, движущегося вокруг Марса по низкой круговой орбите, к периоду обращения аналогичного спутника Земли.

1) 1

2) 2

3) 1,41

4) 2,82

А 4

Масса некоторой планеты в 3 раза меньше массы Земли, а период обращения спутника, движущегося вокруг этой планеты по низкой круговой орбите, совпадает с периодом обращения аналогичного спутника Земли. Отношение средних плотностей планеты и Земли равно

1) 1 2) 2

3) 0,5 4) 0,7

А 1

Ученик измеряет силу кисти своей руки с помощью пружинного силомера. При этом используется способность силы:

А. изменять скорость тела

Б. вызывать деформацию

1) только первое

2) только Б

3) и А, и Б

4) ни А, ни Б

А 2

Согласно закону Гука сила натяжения пружины при растягивании прямо пропорциональна

1) ее длине в свободном состоянии

2) ее длине в натянутом состоянии

3) разнице между длиной в натянутом и свободном состоянии

4) сумме длин в натянутом и свободном состоянии.

А 3

Ученик провел опыты с двумя разными пружинами, измеряя силы упругости при разных ее деформациях. Результаты экспериментов приведены в таблице

Закон Гука в условиях приведенных опытов …

1) подтверждается только для первой пружины

2) подтверждается только для второй пружины

3) подтверждается для обеих пружин

4) не подтверждается ни для одной из пружин

А 4

Пружина жесткости k = 10⁴ Н/м под действием силы 1000 Н растянется на

А 5

Пружина жесткости k = 10⁴ Н/м под действием силы 2000 Н растянется на

А 6

Под действием силы 3 Н пружина удлинилась на 4 см. Чему равен модуль силы, под действием которой удлинение пружины составило 6 см?

1) 3,5 Н 2) 4 Н

3) 4,5 Н 4) 5 Н

А 7

Под действием силы 3 Н пружина удлинилась на 4 см, а под действием силы 6 Н – на 8 см. Чему равен модуль силы, под действием которой удлинение пружины составило 6 см?

1) 3,5 Н 2) 4 Н

3) 4,5 Н 4) 5 Н

А 8

Две пружины растягиваются одинаковыми силами . Жесткость первой пружины в 1,5 раза больше жесткости второй пружины . Удлинение второй пружины равно , а удлинение первой равно

1) 0,5 2) 0,67

3) 1,5 4) 2,0

А 9

Две пружины растягиваются одинаковыми силами . Жесткость первой пружины в 1,5 раза больше жесткости второй пружины . Удлинение первой пружины равно , а удлинение второй равно

1) 0,5 2) 0,67

3) 1,5 4) 2,0

А 10

Две упругие пружины растягиваются одинаковыми силами . Жесткость второй пружины на 50 % меньше жесткости первой пружины . Удлинение второй пружины равно , а удлинение первой равно

1) 0,5 2) 0,67

3) 1,5 4) 2,0

А 11

Н а рисунке представлен график зависимости силы упругости пружины от величины ее деформации. Жесткость этой пружины равна

1) 0,01 Н/м 2) 10 Н/м

3) 20 Н/м 4) 100 Н/м

А 12

На рисунке представлены графики 1 и 2 зависимости модулей сил упругости от деформации для двух пружин. Отношение жесткостей пружин равно

1) 1 2) 2

3) 3 4) 4

А 13

При исследовании упругих свойств пружины ученик получил следующую таблицу результатов измерений силы упругости и удлинения пружины.

Жесткость пружины равна

1) 0,5 Н/м 2) 5 Н/м

3) 50 Н/м 4) 500 Н/м

А 14

В процессе экспериментального исследования жесткости трех пружин получены данные, которые приведены в таблице.

Жесткость пружин возрастает в такой последовательности

1) 1, 2, 3;

2) 1, 3, 2;

3) 2, 3, 1;

4) 3, 1, 2.

А 15

Н а рисунке представлен школьный лабораторный динамометр. Закон Гука для пружины динамометра имеет вид (все единицы даны в СИ). Чему равна сила упругости пружины динамометра при деформации 20 см?

1) 2 Н

2) 8 Н

3) 800 Н

4) при такой деформации динамометр будет испорчен.

А 16

Под действием пружины динамометра брусок движется равномерно по поверхности стола (рис.). По показаниям динамометра ученики могут записать значение действующей силы. Какая запись наиболее правильная?

1) 1,70 Н

2) Н

3) Н

4) Н

А 17

Исследовалась зависимость растяжения жгута от приложенной силы. Погрешность измерения силы и величины растяжения жгута составляли соответственно 0,5 Н и 0,5 см. Результаты измерений с учетом их погрешности представлены на рисунке. Согласно этим измерениям, жесткость жгута приблизительно равна

А 18

Для измерения жесткости пружины ученик собрал установку (см. рис.1), и подвесил к пружине груз массой 0,1 кг (см. рис.2). Какова жесткость пружины?

Рис.1 Рис. 2

А 19

П о результатам исследования построен график зависимости модуля силы упругости от её деформации (см. рисунок). Каким будет удлинение пружины при подвешивании груза массой 2 кг?

1) 8 см 2) 10 см

3) 12 см 4) 16 см

А 20

К пружине школьного динамометра подвешен груз массой 0,1 кг. При этом пружина удлинилась на 2,5 см. Каким будет удлинение пружины при добавлении ещё двух грузов по 0,1 кг?

1) 5 см 2) 7,5 см

3) 10 см 4) 12,5 см

А 21

К пружине школьного динамометра подвешен груз массой 0,1 кг. При этом пружина удлинилась на 2,5 см. Каким будет удлинение пружины при добавлении ещё трёх грузов по 0,1 кг?

1) 5 см 2) 7,5 см

3) 10 см 4) 12,5 см

А 22

Под действием груза пружина удлинилась на 1 см. Этот же груз подвесили к пружине с вдвое большей жесткостью. Удлинение пружины стало равным

1) 0,25 см 2) 0,5 см

3) 1 см 4) 2 см

А 23

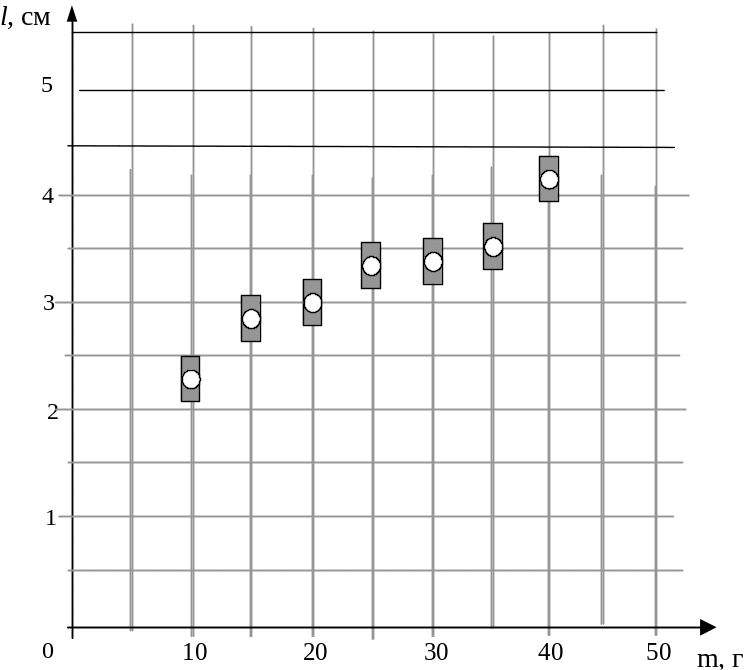
На графике представлены результаты измерения длины пружины при различных значениях массы грузов, лежащих в чашке пружинных весов (см. рисунок).

С учетом погрешностей измерений (Δm = ±1 г, Δl = ± 0,2 см) жесткость пружины k приблизительно равна

А 24

На графике представлены результаты измерения длины пружины при различных значениях массы грузов, лежащих в чашке пружинных весов (см. рисунок).

С учетом погрешностей измерений (Δm = ±1 г, Δl = ± 0,2 см) найдите приблизительную длину пружины при пустой чашке весов.

А 25

На рисунке показан график зависимости силы упругости бельевой резинки от изменения ее длины ∆ . При каких значениях изменения длины ∆ соблюдается закон Гука о пропорциональности силы упругости резинки ее удлинению?

1) при всех значениях ∆

2) при ∆ больше

3) ни при каких значениях ∆

4) при ∆ меньше

А 26

Однородную пружину длиной и жесткостью разрезали пополам. Какова жесткость половины пружины?

1) /2 2)

3) 2 4) 4

А 27

Однородную пружину длиной и жесткостью разрезали на три равные части. Чему равна жесткость каждой части пружины?

1) /3 2)

3) 3 4) 9

А 28

Под действием груза проволока удлинилась на 1 см. Этот же груз подвесили к проволоке такой же длины из того же материала, но имеющей в 2 раза большую площадь сечения. Удлинение проволоки стало

1) 0,25 см 2) 0,5 см

3) 1 см 4) 2 см

А 29

При подвешивании груза массой к стальному тросу длина троса возрастает на от его начального значения . Величина не изменится, если

1) будет вдвое больше, а вдвое меньше

2) и будут вдвое больше

3) и будут вдвое меньше

4) будет вчетверо меньше, а вдвое меньше