Линии на поверхности

1. Асимптотические линии

Опр.: направление на регулярной поверхности в точке называется асимптотическим, если нормальная кривизна поверхности в этом направлении равна нулю.

Таким образом, направление 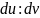будет асимптотическим тогда и только тогда, когда .

В эллиптической точке поверхности не существует асимптотических направлений;

В гиперболической точке – два асимптотических направления;

В параболической точке – одно асимптотическое направление;

В точке уплощения – любое направление является асимптотическим.

Опр.: кривая на поверхности называется асимптотической линией, если ее направление в любой точке является асимптотическим.

Уравнение – дифференциальное уравнение асимптотических линий.

Замечания:

1) Если на поверхности расположена прямая, то она будет асимптотической линией.

2) Касательная плоскость поверхности в любой точке асимптотической линии является соприкасающейся плоскостью.

3) Координатная сеть будет асимптотической тогда и только тогда, когда коэффициенты 2^ой квадратичной формы равны нулю.

Опр.: два направления и 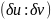в точке поверхности называются сопряженными, если содержащие их прямые и являются сопряженными диаметрами индикатрисы Дюпена в точке .

Чтобы направления 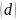и были сопряженными необходимо и достаточно выполнение условия: .

Замечания:

1) Неасимптотическое направление сопряжено с направлением диаметра линии второго порядка, делящего пополам хорды направления .

2) Асимтотическое направление центральной линии второго порядка сопряжено с самим собой.

3) Асимптотическое направление линии параболического типа сопряжено с любым направлением.

2. Линии кривизны

Опр.: линия на поверхности называется линией кривизны, если ее направление в любой точке является главным.

Дифференциальное уравнение линии кривизны:

Опр.: направление на поверхности называется главным, если нормальная кривизна поверхности в этом направлении достигает экстремального значения.

Замечания:

Главные направления – это направления, совпадающие с направлением осей индикатрисы кривизны.

Если главные направления ортогональны и сопряжены, то

1. Условие ортогональности:

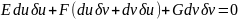
2. Условие сопряженности: ,

где .

Представим эти равенства как систему линейных уравнений относительно переменных , :

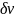- необходимое и достаточное условие главных направлений, сводится к .

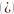Замечания:

Главные направления не определены в двух случаях:

1. В случае точки уплощения, т.к. в этой точке любое направление является главным;

2. В случае омбалической точки (точки, в которой индикатриса Дюпена является окружностью: 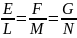) тоже любое направление является главным.

Для координатных линий: и .

3. Геодезические линии

Опр.: кривая на поверхности называется геодезической линией, если у нее в любой точке геодезическая кривизна равна нулю.

Кривизна кривой 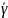в точке называется геодезической кривизной кривой в точке .

Замечание:

Для того чтобы кривая была геодезической линией необходимо и достаточно, чтобы ее главная нормаль в любой точке, где кривизна не равна нулю совпадала с нормалью поверхности.

Геодезическая линия на сфере – большие круги.