
- •Первая квадратичная форма (основная гауссовская дифференциальная форма)
- •Другой способ определения 1ой квадратичной формы.
- •Приложения 1ой квадратичной формы.
- •3) Площадь области на поверхности
- •Вторая квадратичная форма
- •Определение 2ой квадратичной формы поверхности
- •Теорема Менье
- •Главные направления и главные кривизны поверхности
- •Главные направления на поверхности
- •Ортогональность главных направлений
- •Формула Эйлера
- •Полная и средняя кривизны поверхности
- •Линии на поверхности
- •Асимптотические линии
Формула Эйлера
Отнесем поверхность к главным направлениям (т.е. выберем координатную сетку как в предыдущем пункте).
Т.к.
направления ортогональны, то
и кроме этого из уравнений
и
имеем:
 ,
,
 и
и
 .
Тогда
.
Тогда
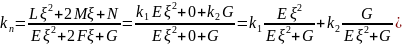
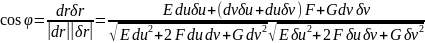
Пусть
угол
 - угол между направлениями
и
.
Поскольку направление задается отношением
дифференциалов, то один из дифференциалов
можно задать произвольно. Пусть
- угол между направлениями
и
.
Поскольку направление задается отношением
дифференциалов, то один из дифференциалов
можно задать произвольно. Пусть
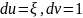 - для первого направления и для второго
направления (вдоль линии
)
-
- для первого направления и для второго
направления (вдоль линии
)
-
 ,
,
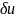 - произвольное. Тогда подставив все это
в формулу нахождения угла между линиями
имеем:
- произвольное. Тогда подставив все это
в формулу нахождения угла между линиями
имеем:
 .
.

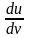

Углы
между направлением
и линией
равен
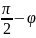 ,
т.е. координатные линии
и
ортогональны. Для него найдем:
,
т.е. координатные линии
и
ортогональны. Для него найдем:
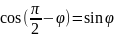
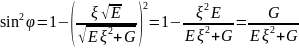
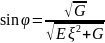
Учитывая полученные правила для тригонометрической функции, имеем (уравнение **):
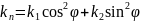 – формула
Эйлера (разложение нормальной кривизны)
– формула
Эйлера (разложение нормальной кривизны)
Из формулы следует:
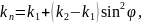
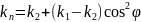
Т.е.,
если
 ,
то
,
то
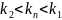 ;
;
если
 ,
то
,
то
 .
.
В обоих случаях нормальная кривизна заключена между главными кривизнами. Главные кривизны являются экстремальными значениями нормальной кривизны.
Полная и средняя кривизны поверхности
Главные
кривизны – инварианты поверхности,
т.е. в неособых точках не зависят от
координатной сетки на поверхности.
Поэтому они важны при изучении поверхности.
Неудобство главных кривизн состоит в
том, что они как корни квадратного
уравнения
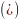 иррационально выражаются через
коэффициенты квадратных форм. Поэтому
составляют два других инварианта – их
произведение
иррационально выражаются через
коэффициенты квадратных форм. Поэтому
составляют два других инварианта – их
произведение
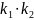 и их сумму
и их сумму
 .
.
Первый из этих новых инвариантов называют полной гауссовской кривизной поверхности, а второй – средней кривизной поверхности. По теореме Виета получаем:
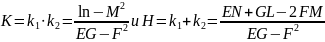
Эти коэффициенты уже есть рациональные функции от коэффициентов квадратичных форм.
Опр.: поверхность, средняя кривизна которой во всех точках равна нулю, называется минимальной поверхностью.
Примеры: 1) плоскость; 2) среди поверхностей вращения – катеноид; 3) среди линейных поверхностей – винтовая поверхность.
Типы точек на поверхности
Тип
точки на поверхности зависит от знака
гауссовской полной кривизны
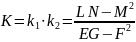 .
Учитывая, что знаменатель правой части
всегда положителен, имеем:
.
Учитывая, что знаменатель правой части
всегда положителен, имеем:
Если
 (
(
 в точке
)
точка
называется эллиптической;
в точке
)
точка
называется эллиптической;Если
 (
(
 в точке
)
точка
называется гиперболической;
в точке
)
точка
называется гиперболической;Если
 (
(
 в точке
)
в точке
)
Следствие
1:
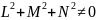 ,
то точка
называется параболической;
,
то точка
называется параболической;
Следствие
2:
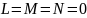 ,
то точка
называется точкой уплощения.
,
то точка
называется точкой уплощения.
Индикатриса Дюпена
Отложим
из произвольной точки
 ,
принадлежащей поверхности в
,
принадлежащей поверхности в
 направлении
отрезок, равный
направлении
отрезок, равный
 ,
где
- нормальная кривизна поверхности в
этом направлении.
,
где
- нормальная кривизна поверхности в
этом направлении.
Опр.:
геометрическое место концов всех этих
отрезков называется индикатрисой
кривизны поверхности в точке
 (или индикатрисой Дюпена).
(или индикатрисой Дюпена).





Найдем
уравнения индикатрисы. Введя в касательной
плоскости поверхности в точке
декартову прямоугольную систему
координат, где оси координат направлены
вдоль векторов
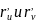 (базис).
За начало координат возьмем точку
касания.
(базис).
За начало координат возьмем точку
касания.
Пусть
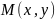 - точка индикатрисы кривизны, соответствующая
направлению
.
Следовательно
- точка индикатрисы кривизны, соответствующая
направлению
.
Следовательно
 .
Вектор
.
Вектор
 - единичный касательный вектор выбранного
направления. По построению
- единичный касательный вектор выбранного
направления. По построению
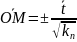 .
.
Тогда

 .
Учитывая, что
.
Учитывая, что
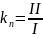 и
и
 ,
получим
,
получим
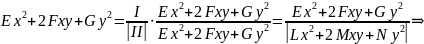
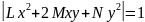 – это
и есть индикатриса Дюпена.
– это
и есть индикатриса Дюпена.
Замечание:
Индикатриса
кривизны представляет собой эллипс в
эллиптичкской точке
 ,
пару сопряженных гипербол – в
гиперболической точке
,
пару сопряженных гипербол – в
гиперболической точке
 и пару параллельных прямых
и пару параллельных прямых
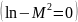 .
.
Соприкасающийся параболоид поверхности
Рассмотрим поверхность класса
 (дважды
регулярную) в окрестности точки
(дважды
регулярную) в окрестности точки
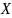 .
Введем ДПСК, выбрав точку
за начало координат, а касательную
плоскость в этой точке
за координатную плоскость
.
Введем ДПСК, выбрав точку
за начало координат, а касательную
плоскость в этой точке
за координатную плоскость
 .
Ось
.
Ось
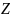 направим по нормали к поверхности в
точке
.
Тогда в выбранной системе координат
имеем (при задании поверхности явным
уравнением
в некоторой точке
):
направим по нормали к поверхности в
точке
.
Тогда в выбранной системе координат
имеем (при задании поверхности явным
уравнением
в некоторой точке
):
 (из уравнения касательной плоскости).
(из уравнения касательной плоскости).
Раскладывая
по формуле Тейлора функцию
 в
окрестности
точки
в
окрестности
точки
 ,
получаем:
,
получаем:

С

 точностью до бесконечно малых более
высокого порядка функцию
можно заменить ее числовой частью:
точностью до бесконечно малых более
высокого порядка функцию
можно заменить ее числовой частью:
 .
График
.
График
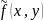 в общем случае является параболоид.
Потому поверхность, заданная уравнением
в общем случае является параболоид.
Потому поверхность, заданная уравнением
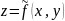 называется соприкасающимся параболоидом
поверхности в точке
.
называется соприкасающимся параболоидом
поверхности в точке
.





Замечание:
Т.к.
первые и вторые производные функций
и
в т. совпадают (коэффициенты 1ой
и 2ой
квадратичных форм выражаются только
через первые и вторые производные
функции), то в точке
у поверхности и ее соприкасающегося
параболоида одинаковые квадратичные
формы, а значит и все геометрические
характеристики, выражающиеся через
них.
совпадают (коэффициенты 1ой
и 2ой
квадратичных форм выражаются только
через первые и вторые производные
функции), то в точке
у поверхности и ее соприкасающегося
параболоида одинаковые квадратичные
формы, а значит и все геометрические
характеристики, выражающиеся через
них.
Деривационные формулы.
Аналогом
формул Френе для поверхностей являются
деривационные формулы. Эти формулы
связывают производные от вектор-функций
 через эти векторы и коэффициенты 1ой
и 2ой
квадратичных форм. Т.к. векторы
- линейно независимы, то имеет место
представления:
через эти векторы и коэффициенты 1ой
и 2ой
квадратичных форм. Т.к. векторы
- линейно независимы, то имеет место
представления:


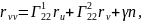


Замечание:
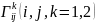 - коэффициенты Кристоффеля.
- коэффициенты Кристоффеля.
Т.к. , то
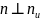 и
и

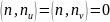 .
Тогда
.
Тогда

 .
Аналогично получим, что
.
Аналогично получим, что
 .
.Т.к.
 ,
то
,
то
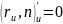 или
или

 .
Аналогично
.
Аналогично
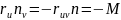 .
Т.к.
.
Т.к.
 ,
то
,
то
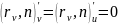
 ,
,
 .
.
Поэтому
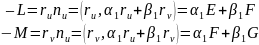
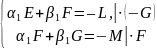

Аналогично:


Для коэффициентов Кристоффеля:


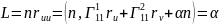 .
Аналогично
.
Аналогично
 и
и
 .
Таким образом, найдены все коэффициенты
деривационных формул.
.
Таким образом, найдены все коэффициенты
деривационных формул.
Основные уравнения теории поверхностей
Пусть
поверхность класса
 (трижды регулярная), а также
(трижды регулярная), а также
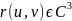 .
Т.к.
- трижды дифференцируемая, то по теореме
Эйлера:
.
Т.к.
- трижды дифференцируемая, то по теореме
Эйлера:
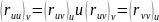 ,
а также
,
а также
 .
.
Используя деривационные формулы, будем иметь:


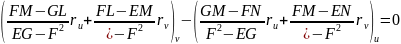
Если в полученных уравнениях произвести дифференцирование и опять воспользоваться деривационными формулами, то получим уравнения:

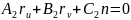

Коэффициенты этих уравнений зависят только от коэффициентов 1ой и 2ой квадратичной формы и их производных. Т.к. векторы - линейно независимые, то получим девять скалярных равенств. Оказывается из этих девяти равенств различных только три. Они и являются основными уравнениями теории поверхности. Это уравнения: Петерсона – Кодацци и формула Гаусса. Эти уравнения показывают связь между коэффициентами 1ой и 2ой квадратичной формы гладкой поверхности класса (других связей нет).
Теорема Бонне:
Пусть
в открытой области
 на плоскости переменных
заданы две произвольные квадратичные
формы:
на плоскости переменных
заданы две произвольные квадратичные
формы:
 и
и
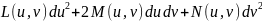 ,
из которых 1ая
положительно определена и коэффициенты
ее принадлежат классу
,
а коэффициенты 2ой
формы принадлежат классу
,
из которых 1ая
положительно определена и коэффициенты
ее принадлежат классу
,
а коэффициенты 2ой
формы принадлежат классу
 .
Тогда, если коэффициенты заданных форм
удовлетворяют условиям Петерсона –
Кодацци и Гаусса, то у любой точки
.
Тогда, если коэффициенты заданных форм
удовлетворяют условиям Петерсона –
Кодацци и Гаусса, то у любой точки
 найдется такая окрестность
найдется такая окрестность
 ,
что существует
- гладкое отображение
,
что существует
- гладкое отображение
 ,
задающее поверхность класса
,
для которой данные квадратичные формы
являются соответственно 1ой
и 2ой
квадратичной формами. Эта поверхность
единственна с точностью до перемещения.
,
задающее поверхность класса
,
для которой данные квадратичные формы
являются соответственно 1ой
и 2ой
квадратичной формами. Эта поверхность
единственна с точностью до перемещения.
