3. Теорема Менье

Рассмотрим на поверхности множество линий , имеющих общую точку и общую касательную в этой точке. Тогда все их главные кривизны одинаковы.

Н айдем связь между их кривизнами .

Выделим линию, лежащую в нормальном сечении поверхности в точке (сечении, проходящем через нормаль и поверхность в точке ) – это линия . Пусть и - кривизна и орт главной нормали этой линии. Вектор главной нормали коллинеарен вектору нормали , т.е. 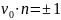. Тогда нормальная кривизна линии : .

Пусть 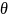- угол между соприкасающейся плоскостью линии и нормалью к поверхности (т.е. угол между векторами нормали).

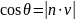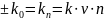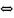
Тогда и , в силу неотрицательности кривизны: . Переходя к обратной величине ( и 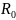- радиусы кривизны линии).

Теорема Менье:

Чтобы получить в данной точке радиус кривизны некоторой линии , лежащей на поверхности, надо умножить радиус кривизны нормального сечения, проходящего через ту же точку и имеющего в ней общую с линией касательную, на косинус угла между соприкасающейся плоскостью линии и нормалью поверхности в указанной точке.

Главные направления и главные кривизны поверхности

Рассмотрим параметризованную поверхность и линию, проходящую через точку . Преобразуем орт касательной к этой линии, проведенный в точке : . Используя 1^ую квадратичную форму, получим: .

Т.к. точка фиксирована, то определены в этой точке, значит для указания направления касательной надо знать отношение .

Замечание:

Говорят, что отношение дифференциалов определяет в данной точке поверхности направление.

1. Главные направления на поверхности

Будем искать направления на поверхности (в фиксированной точке ) в которых нормальные кривизны достигают экстремального значения. Обозначая 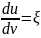и учитывая, что имеем (из условия )

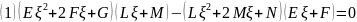
или

Дискриминант уравнения 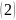неотрицателен (равен нулю, когда уравнение обращается в тождество), поэтому оно имеет два различных действительных корня . Определяемые этими корнями направления и называются главными, а соответствующие им нормальные кривизны – главными кривизнами поверхности.

Другой способ нахождения главных кривизн: разделим уравнение на :

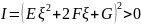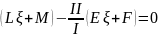
или

Перепишем по-другому уравнение :

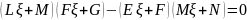
Разделим на 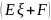, учитывая что 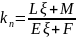, получаем:

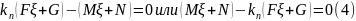
Исключая 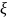из уравнений :

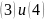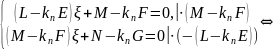
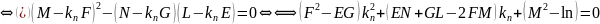
Корни последнего уравнения и будут главными кривизнами.

2. Ортогональность главных направлений

Выберем координатную сетку так, чтобы в любых точках линии 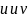касались главных направлений. Тогда нормальные кривизны линий будут главными кривизнами.

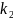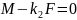Пусть - нормальная кривизна линии . Т.к. вдоль этой линии не изменяется, то . Из уравнений и получаем: и .

Аналогично, если - нормальная кривизна линии , то вдоль этой линии не изменяется, то . Из уравнений и получаем: и

Приравнивая первое равенство уравнения и второе равенство уравнения 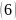, получаем:

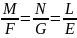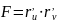или . Но , т.к. в противном случае из уравнений и следует, что . А это означает, что уравнение - тождество и главные направления не определяются. Поэтому: , а т.к. коэффициент , направления которых в нашем случае совпадают с главными направлениями, поэтому эти вектора, а значит и главные направления ортогональны.