- •Первая квадратичная форма (основная гауссовская дифференциальная форма)
- •Другой способ определения 1ой квадратичной формы.
- •Приложения 1ой квадратичной формы.
- •3) Площадь области на поверхности
- •Вторая квадратичная форма
- •Определение 2ой квадратичной формы поверхности
- •Теорема Менье
- •Главные направления и главные кривизны поверхности
- •Главные направления на поверхности
- •Ортогональность главных направлений
- •Формула Эйлера
- •Полная и средняя кривизны поверхности
- •Линии на поверхности
- •Асимптотические линии
Первая квадратичная форма поверхности
С
регулярной поверхностью класса
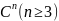 связаны две квадратичные формы. Первая
квадратичная форма (ее еще называют
метрикой поверхности) связана с внутренней
геометрией поверхности.
связаны две квадратичные формы. Первая
квадратичная форма (ее еще называют
метрикой поверхности) связана с внутренней
геометрией поверхности.
Опр.: к внутренней геометрии поверхности относятся те понятия и факты, которые не меняются при изгибании поверхности. Эти понятия и факты определяются первой квадратичной формой.
Квадратичные формы
Пусть
задано линейно-векторное пространство
 .
.
Опр
1: говорят, что в этом пространстве
определена линейная форма
 ,
если каждому элементу
,
если каждому элементу
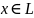 поставлено в соответствие число и при
этом выполняются следующие свойства:
поставлено в соответствие число и при
этом выполняются следующие свойства:
 ,
где
,
где
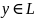 ,
– аддитивности;
,
– аддитивности; ,
где
,
где
 - число, - однородности
- число, - однородности
 говорят
о линейности
.
говорят
о линейности
.
Примеры:
проекции вектора
 на ось
на ось
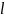 ,
т.е.
,
т.е.
Опр
2: под билинейной формой понимают
скалярную функцию двух аргументов
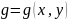 линейную по каждой из своих аргументов,
т.е.
линейную по каждой из своих аргументов,
т.е.

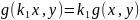 ,
,
 - число
- число
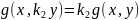
Примеры:
скалярное произведение двух векторов:

Если
в пространстве
выбрана система координат с базисом
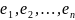 ,
то линейную и билинейную формы можно
записать в этом базисе следующим образом:
,
то линейную и билинейную формы можно
записать в этом базисе следующим образом:
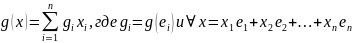
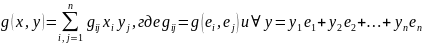
Здесь
 - вектор линейной формы и
- вектор линейной формы и
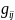 - матрица билинейной формы, числа
- матрица билинейной формы, числа
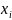 и
и
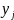 - координаты векторов
и
- координаты векторов
и
 в выбранном базисе.
в выбранном базисе.
Опр
3: билинейная форма
 называется симметричной, если
называется симметричной, если
 и кососимметрической, если
и кососимметрической, если
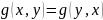 .
.
Для
того чтобы билинейная форма была
симметричной необходимо и достаточно,
чтобы ее матрица была симметрична, т.е.
 .
.
Для
каждой симметричной билинейной формы
можно построить единственным образом
квадратичную форму, отождествляя ее
аргументы, тогда получим:
 при
при
 .
.
Опр
4: функция
 называется квадратичной формой и в
выбранном базисе ее можно представить:
называется квадратичной формой и в
выбранном базисе ее можно представить:

Матрица - симметричная. Можно в пространстве найти базис, в котором квадратичная форма, имеет вид:
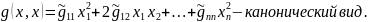
Замечание: существует базис в пространстве , в котором квадратичная форма имеет специальный наиболее простой канонический вид:
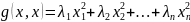
Первая квадратичная форма (основная гауссовская дифференциальная форма)
Линейный элемент.
В декартовой системе координат:


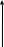

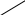

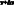








В аффинной системе координат:








На регулярной поверхности:



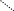


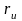





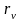


При
бесконечно малом приращении
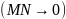 криволинейный
криволинейный
 можно рассматривать как прямолинейный,
т.е.
можно рассматривать как прямолинейный,
т.е.
 ,
,

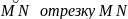 (как хорды стягивающие дуги). Тогда
(как хорды стягивающие дуги). Тогда

Если
поверхность параметризована вектор-функцией
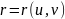 ,
то
,
то
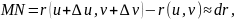
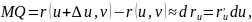

Получаем,
что

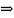

Замечание:
Вместо
 ,
,
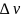 можно ставить
можно ставить
 и
и
 получаем дифференциальную форму:
получаем дифференциальную форму:


Уравнения
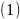 называется 1ой
квадратичной формой, если ввести
следующие коэффициенты:
называется 1ой
квадратичной формой, если ввести
следующие коэффициенты:

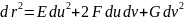
И
учитывая, что
 ,
окончательно получим:
,
окончательно получим:
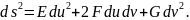
Замечание:
Квадратичная форма представляет двумерный вариант метрики поверхности. Первая квадратичная форма не определяет однозначно форму поверхности.
Метрические коэффициенты
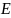 ,
,
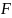 и
и
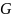 определяют не только длины всех кривых
на поверхности, но и вообще результат
всех измерений на поверхности.
определяют не только длины всех кривых
на поверхности, но и вообще результат
всех измерений на поверхности.Все геометрические величины, которые определяются только при помощи коэффициентов первой квадратичной формы, не меняются при изгибаниях поверхности и являются внутренне геометрическими.
Другой способ определения 1ой квадратичной формы.
Опр.: дифференциальной формой называется всякий однородный многочлен относительно дифференциалов – аргументов:
Полный дифференциал
 радиус-вектора
радиус-вектора
 текущей точки поверхности является
инвариантной линейной дифференциальной
формой:
текущей точки поверхности является
инвариантной линейной дифференциальной
формой:
 .
Тем же свойством инвариантности обладает
и скалярный квадрат этой формы.
.
Тем же свойством инвариантности обладает
и скалярный квадрат этой формы.Опр.: скалярный квадрат полного дифференциала радиус-вектора текущей точки поверхности называется 1ой квадратичной формой поверхности:

Свойства 1ой квадратичной формы:
Первая квадратичная форма поверхности является положительно определенной.
Опр.:
квадратичная форма называется положительно
определенной, если
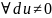 и
и
 имеем
имеем
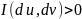 .
.
Действительно,
если
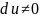 и
и
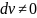 ,
то
,
то
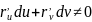 ,
т.е. векторы
,
т.е. векторы
 и
и
 - линейно независимые, поэтому
- линейно независимые, поэтому
 .
.
С
другой стороны, можно показать,
“дискриминант” 1ой
квадратичной формы
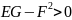 ,
т.к.
,
т.к.

Значит поэтому 1ая квадратичная форма положительно определена.
Первая квадратичная форма не зависит от выбора параметризации поверхности.
Следствия:
Если поверхность задана параметрически:
 тогда:
тогда:
 и
и
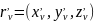

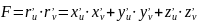 и
и

В случае явного задания поверхности:
 получаем (пусть
получаем (пусть
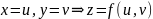 )
и используя предыдущее следствие:
)
и используя предыдущее следствие:

Геометрический смысл коэффициентов 1ой квадратичной формы






Коэффициент :
 .
Коэффициент
есть квадрат производной длины дуги
координатной линии
.
Коэффициент
есть квадрат производной длины дуги
координатной линии
 по ее же параметру.
по ее же параметру.Коэффициент :
 коэффициент
есть квадрат производной длины дуги
координатной линии
коэффициент
есть квадрат производной длины дуги
координатной линии
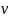 по ее же параметру.
по ее же параметру.Коэффициент :
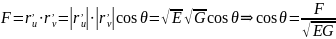 ,
если
,
если
 координатные линии ортогональны в
данной точке.
координатные линии ортогональны в
данной точке.
Замечание:
знак коэффициента
зависит от
 .
.
Вывод: коэффициент используется для вычисления угла между координатными линиями.