Нелинейные структуры

В качестве примеров нелинейных структур рассмотрим

1. спи­ски;

2. деревья;

3. сети.

Порядок следования (и, соответственно, выборки) элементов таких структур может не соответствовать порядку расположения элементов в памяти.

Списки представляют собой пример линей­ного упорядочения, деревья - двумерного, сети - произвольно­го.

Соответственно различаются методы и средства, обеспечи­вающие последовательность выборки элементов данных. Обычно для обеспечения возможности прямого доступа к произвольному элементу необходимо использовать вспомогательные структуры типа инвертированных списков.

Списки. Как и массив, список представляет собой совокуп­ность однотипных элементов. Однако порядок выборки элемен­тов может отличаться от порядка следования в памяти, опреде­ленного при размещении.

Наиболее очевидный способ установ­ления однонаправленного порядка выборки элементов - это сопоставить каждому элементу списка ссылку, указывающую на следующий элемент.

Соответственно, для организации двуна­правленного списка, допускающего также выборку в обратном порядке, каждый элемент должен иметь ссылку на предыдущий. Такая организация уже не допускает возможности прямого дос­тупа, например, по номеру элемента.

Кроме того, число элементов списка, как и в случае последо­вательностей, может быть неизвестно до размещения, и до нача­ла обработки (и, соответственно, размещения) необходимо счи­тать длину списка бесконечной, что ведет к необходимости пре­дусматривать специальную процедуру выделения/освобождения памяти.

Таким образом, с точки зрения физической реализации эле­мент списка должен быть составным, включающим собственно информативные данные, несущие смысловое значение, и допол­нительные данные (ссылки), определяющие порядок доступа к информативным элементам.

Понятие списка достаточно универсально. В общем случае ссылки могут указывать ответвления к другим спискам - под­спискам. В зависимости от способа построения списка и предпо­лагаемых путей доступа к элементам различают следующие виды ссылок: перекрестные, боковые, иерархические, множественные, что позволяет изменять «естественный» последовательный поря­док прохода по элементам списка.

Д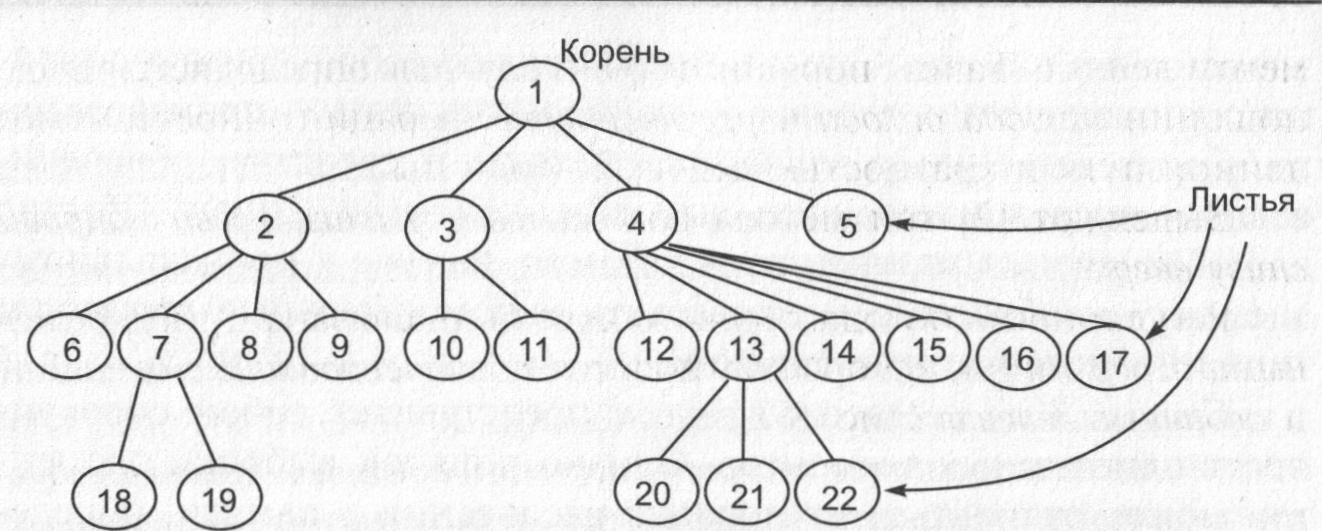 еревья. Дерево (рис. 3) представляет собой иерархию эле­ментов, называемых узлами. На самом верхнем уровне иерархии имеется только один узел - корень.

Рис. 3. Пример структуры типа дерево

Каждый узел, кроме корня, связан с одним узлом на более высоком уровне, называемым исходным узлом для данного узла. Каждый элемент имеет только один исходный. Каждый элемент может быть связан с одним или несколькими элементами на более низком уровне, которые называются порожденными. Элементы, расположенные в конце ветви, т. е. не имеющие порожденных, называются листьями.

На практике существуют различные способы представления структур деревьев.

Сетевые структуры

Иерархические структуры характерны для многих областей, однако во многих случаях отдельная запись требует более одного представления или связана с несколькими другими.

В результате получаются обычно более сложные структуры по сравнению с древовидными. Например, генеалогическое дерево может быть представлено в виде древовидной структуры, только если для ка­ждого элемента (личности) будет показан только один исходный элемент (родитель). Если бы были показаны оба родителя, то это была бы более сложная структура.

В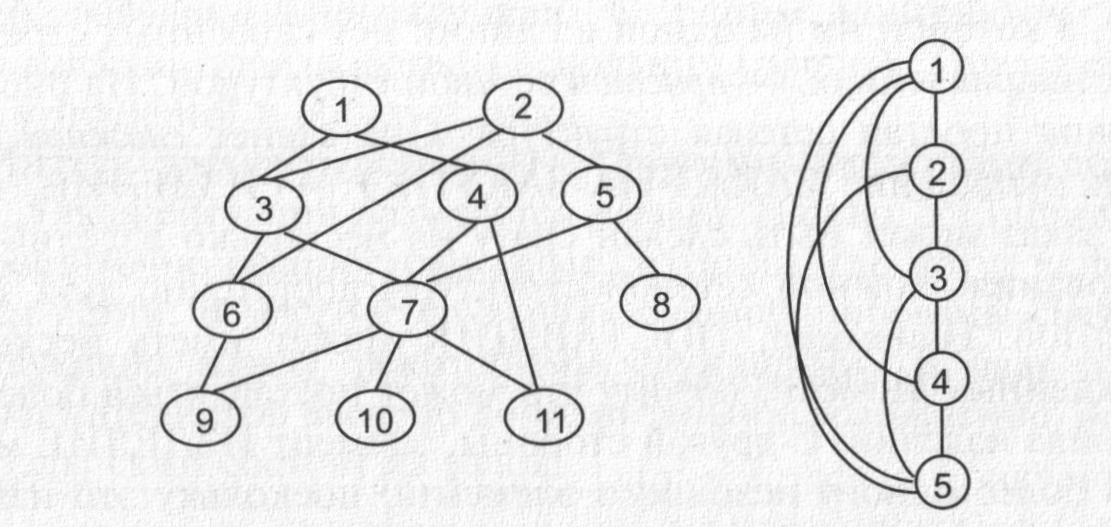 сетевой структуре любой элемент может быть связан с лю­бым другим элементом. Примеры сетевых структур приведены на рис. 5.

Рис. 5. Примеры сетевых структур

Так же, как и в случае древовидных структур, сетевую струк­туру можно описать с помощью исходных и порожденных эле­ментов.

Удобно представлять ее так, чтобы порожденные эле­менты располагались ниже исходных. При рассмотрении неко­торых сетевых структур естественно говорить об уровнях, так же как и в случае древовидных структур.

Во многих сетевых структурах, задающих связи между эле­ментами, представление отношений между исходными и порож­денными элементами аналогично представлению отношений в случае дерева: отношение исходный - порожденный является сложным (указывается сдвоенными стрелками), а отношение по­рожденный - исходный - простым (указывается одинарными стрелками).

Пример приведен на рисунке 6.