Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ковровская государственная технологическая академия

имени В.А. Дегтярева»

Интегралы. Дифференциальные уравнения.

Контрольная работа по математике для заочного отделения.

Миронова Е.А.

Юлина Н.А.

г. Ковров 2013 г.

Методические указания предназначены в качестве пособия для студентов заочного отделения технических специальностей. Содержат в себе сжатый теоретический материал и индивидуальные задания к контрольной работе по математике, а так же решение типового варианта.

1. Интегральное исчисление функции одного действительного аргумента.

1.1. Неопределённый интеграл.

Функция называется первообразной функции , если на и определена и непрерывна на . Если – первообразная для функции , то множество функций называется неопределённым интегралом от функции и обозначается символом

,

где – подынтегральная функция, – подынтегральное выражение, а – переменная интегрирования.

Восстановление функции по её производной называется интегрированием.

Основные свойства неопределённого интеграла.

1. .

2. .

3. .

4. , .

5. .

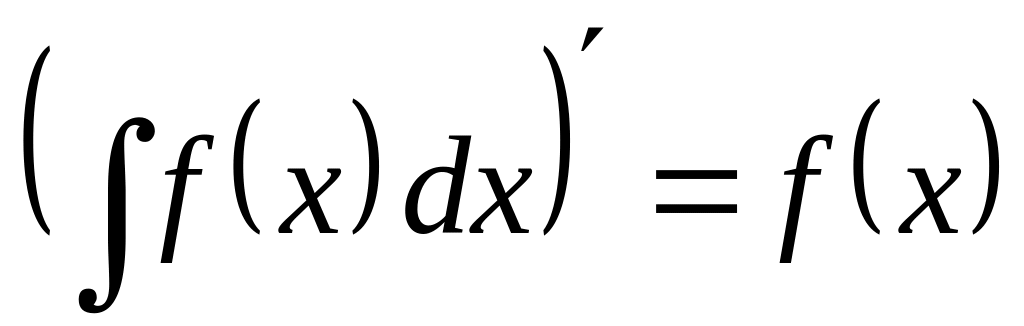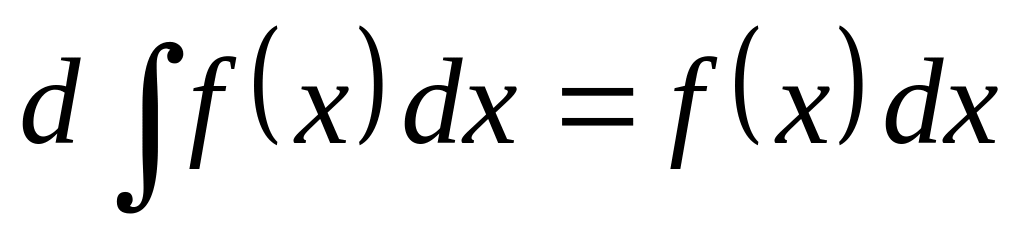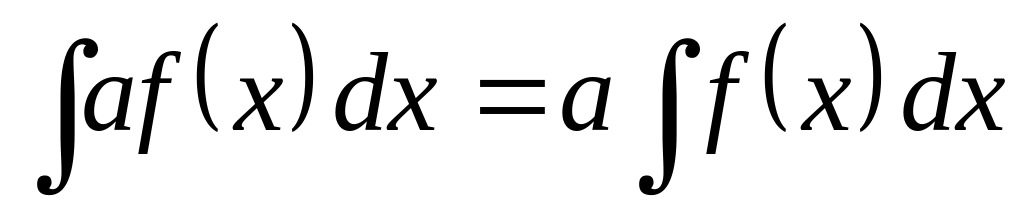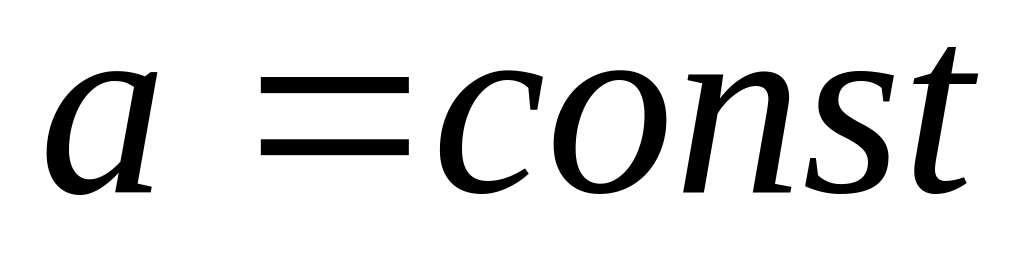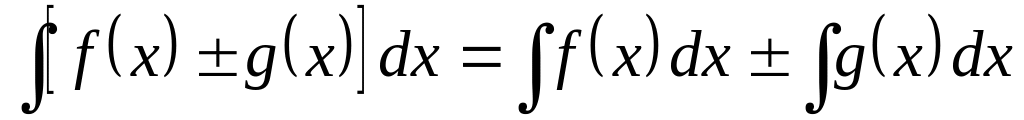6. Если и 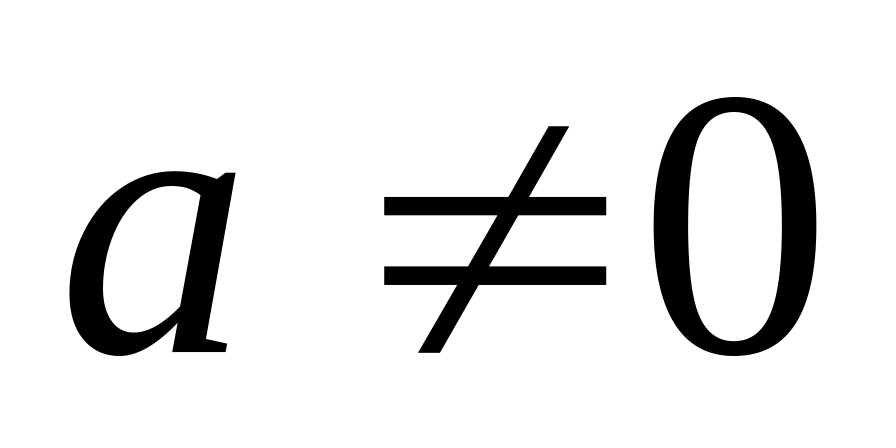, то .

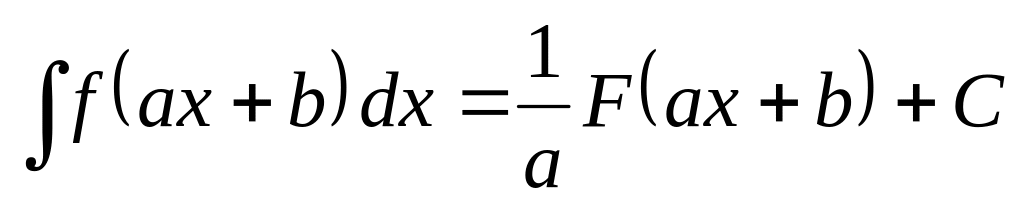Основные интегралы от элементарных функций:

1. 

2. ,

3. 

4. ,

5. ,

6. ,

7. 

8. 

9. ,

10. ,

11. 

12. 

13. 

14. ,

15. 

16. ,

17. ,

18. ,

19. 

20. ,

21. 

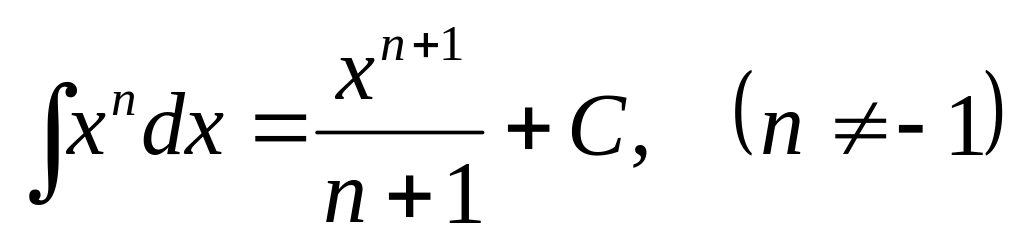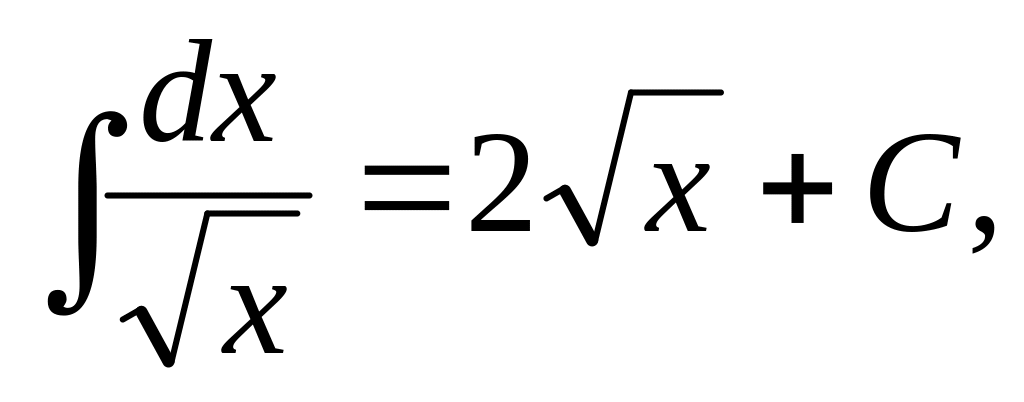
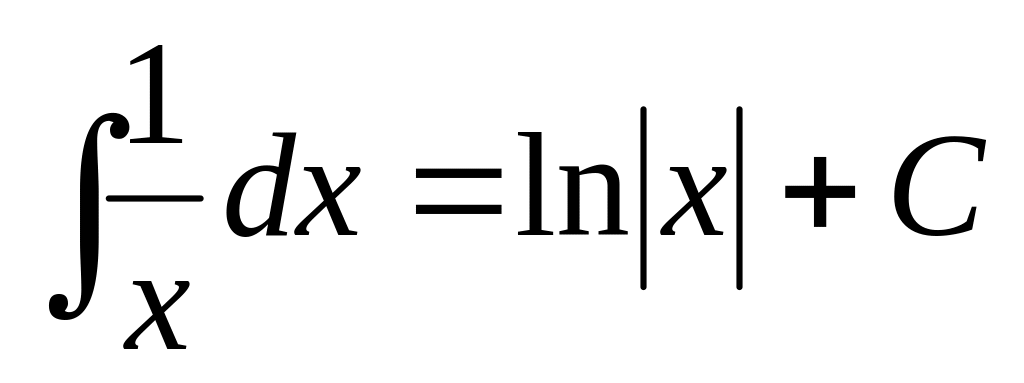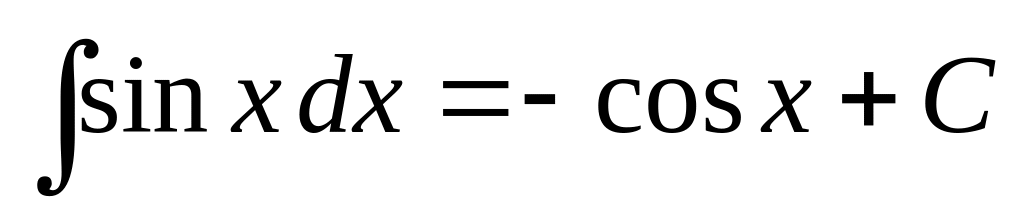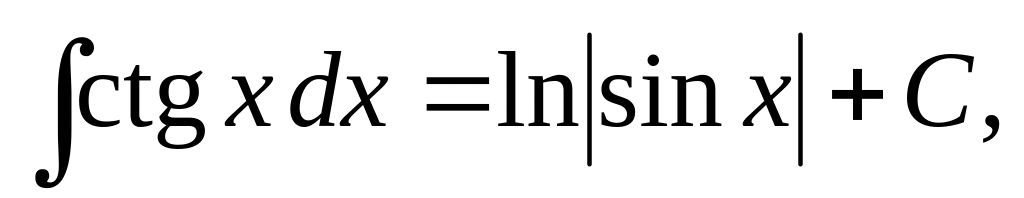
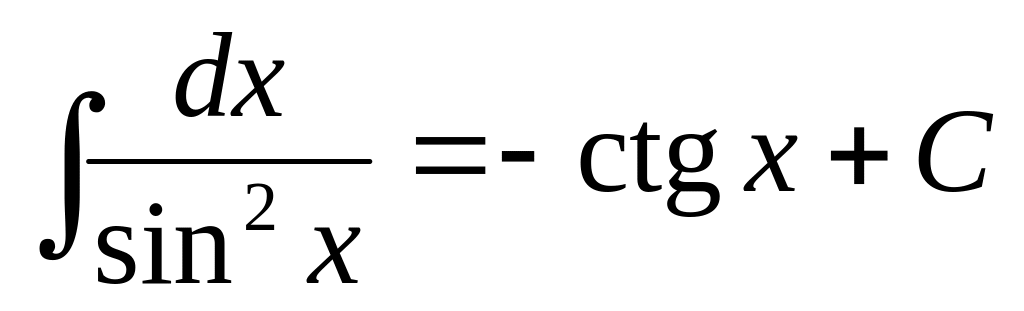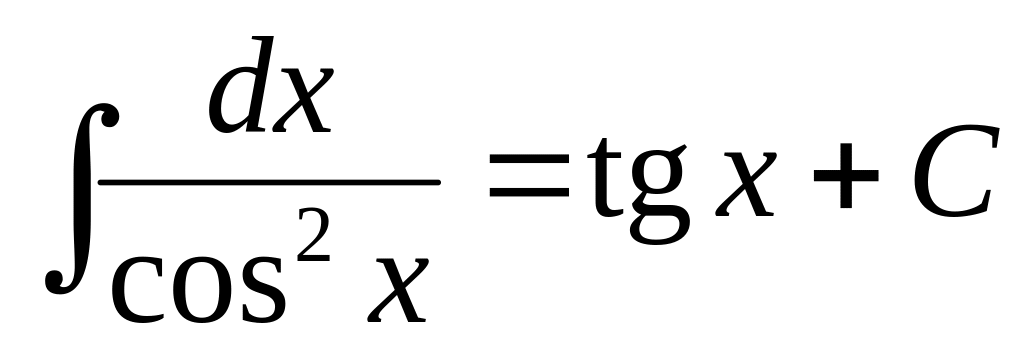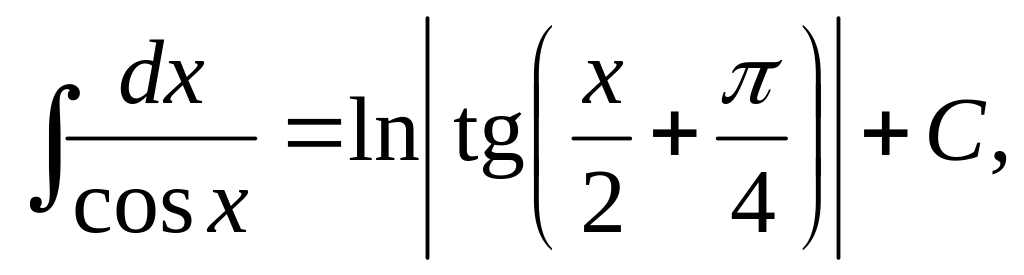
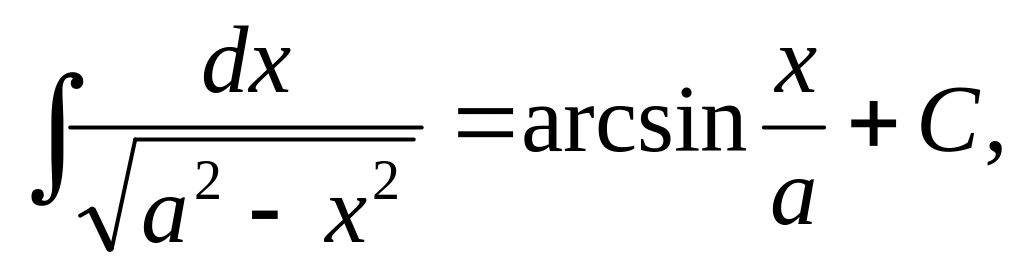
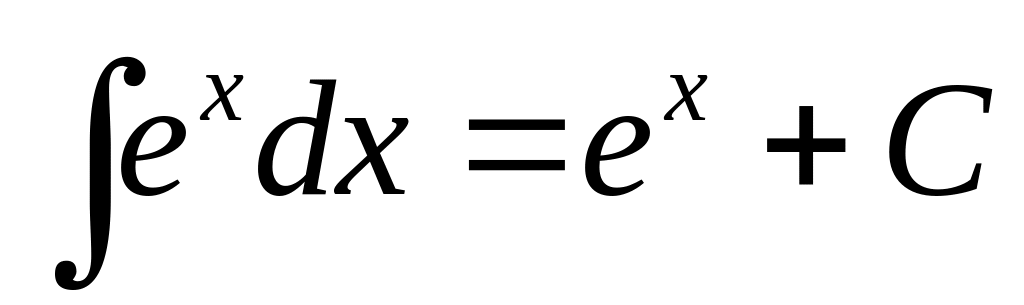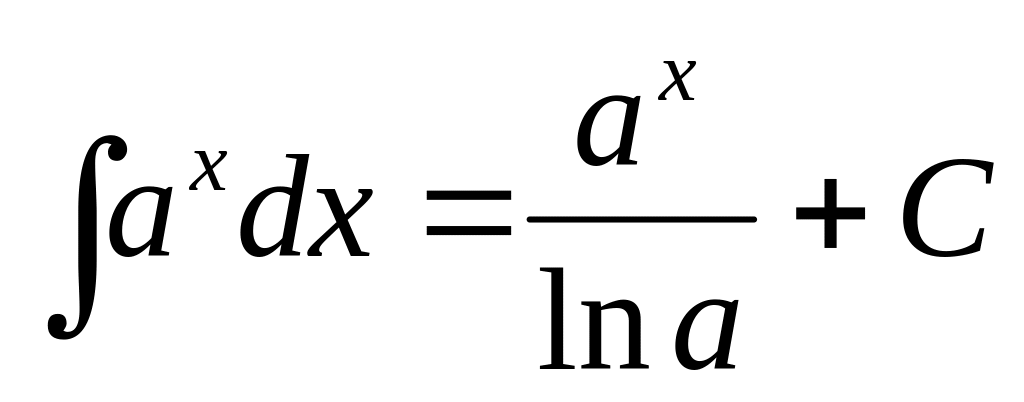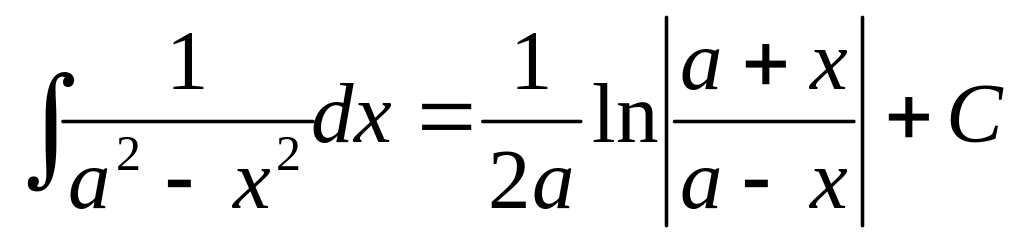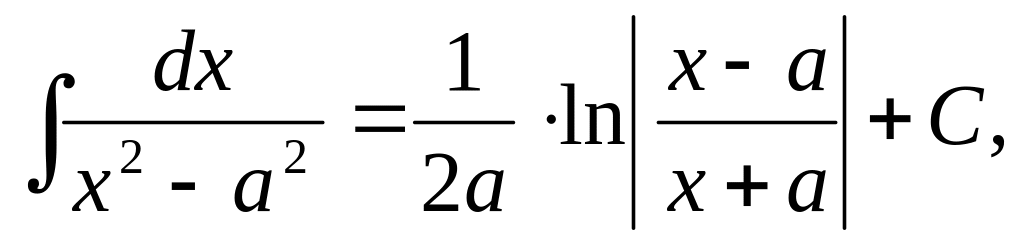
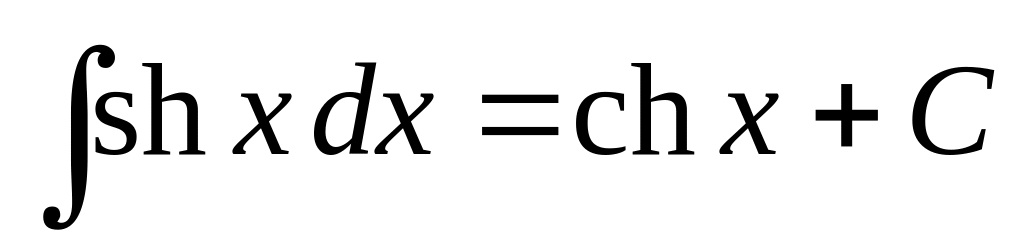Рассмотрим основные методы интегрирования.

Непосредственное интегрирование – это метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применение свойств неопределенного интеграла приводится к табличному интегралу.

Замена переменной. Если – непрерывно дифференцируемая функция и , то

. (1.1)

Интегрирование по частям. Пусть и непрерывно дифференцируемые функции, тогда

. (1.2)

1.2 Определённый интеграл.

Пусть функция определена на отрезке . Разобьём этот отрезок на n произвольных частей точками .

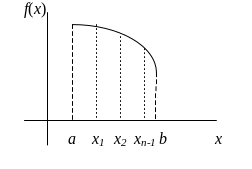
Рис. 17

В каждом из полученных частичных отрезков выберем произвольную точку и составим сумму:

,

где . Эта сумма называется интегральной суммой для функции на . Обозначим (т.е. длина наибольшего частичного отрезка).

Если существует конечный предел I интегральной суммы  при , то этот предел называется определённым интегралом от функции по и обозначается

.

В этом случае называется интегрируемой на . Числа a и b называются соответственно нижним и верхним пределом интегрирования.

Основные свойства определённого интеграла.

1. ,

2. ,

3. ,

4. , ,

5. ,

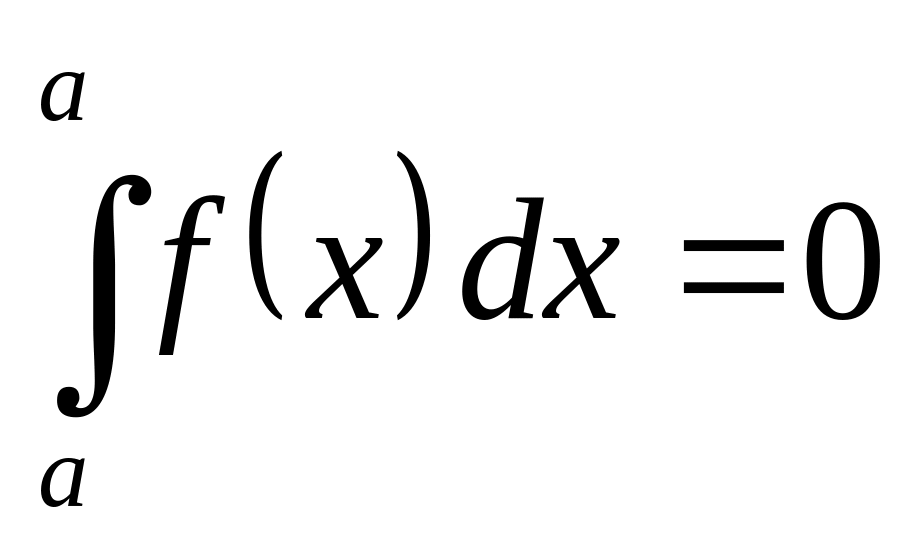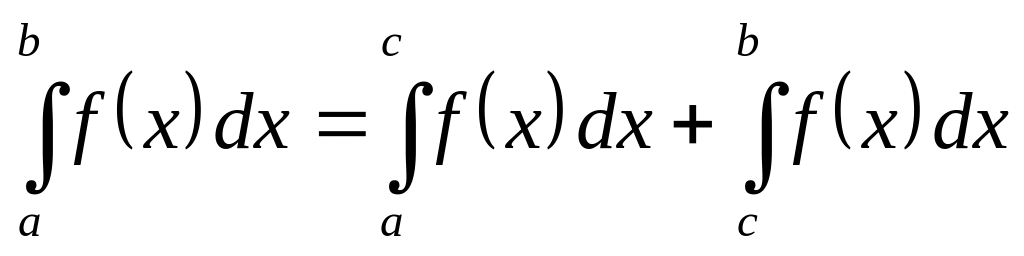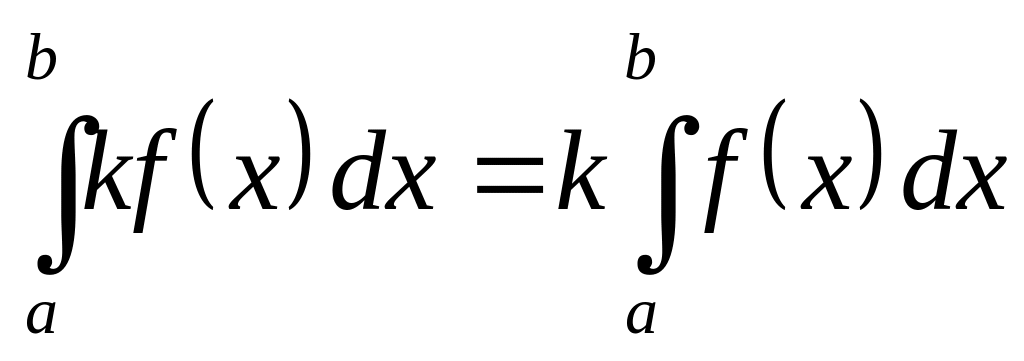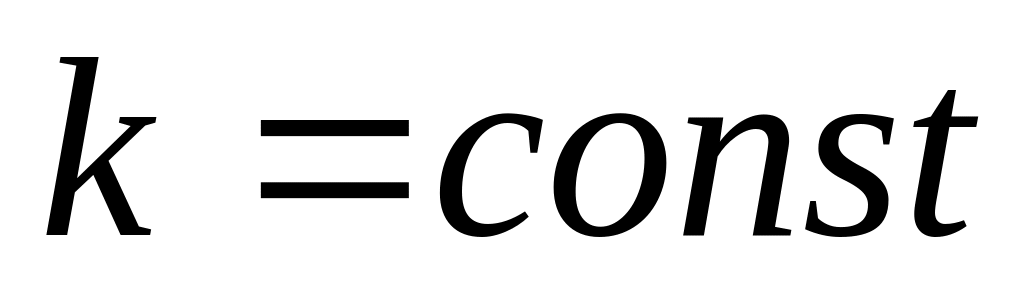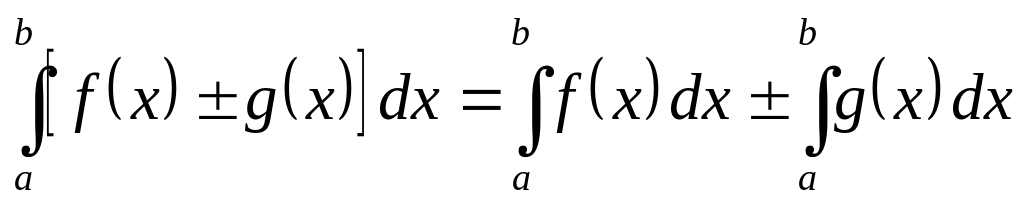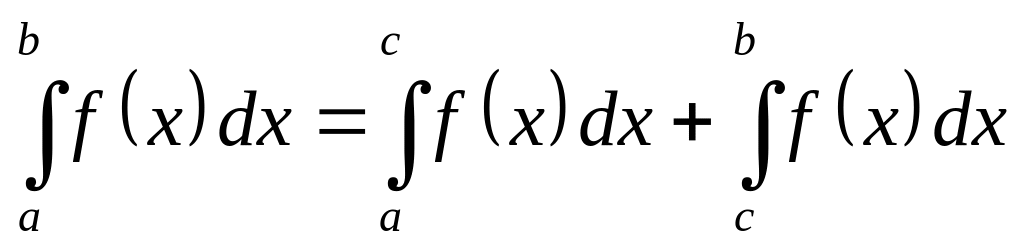6. , где .

Основные методы интегрирования.

Формула Ньютона-Лейбница. Если функция определена и непрерывна на отрезке , а – её первообразная, т.е. , то

. (1.3)

Формула интегрирования по частям. Если и – непрерывно интегрируемы на функции, то

. (1.4)

Замена переменной. Если функция непрерывна на отрезке , – непрерывно дифференцируемая функция на , где , и определена и непрерывна на , то

. (1.5)

Определённый интеграл применяют для вычисления площади криволинейной трапеции. Если криволинейная трапеция ограничена сверху графиком функции , слева и справа – прямыми и , снизу – осью Ох, то площадь вычисляется по формуле

. (1.6)

Площадь криволинейной фигуры, ограниченной сверху графиком функции , снизу – графиком функции , слева и справа – прямыми и , вычисляется по формуле

. (1.7)

Определенный интеграл с бесконечным пределом интегрирования называется несобственным интегралом. Пусть функция непрерывна на интервале , тогда несобственный интеграл имеет вид:

. (1.8)

К несобственным относятся так же и интегралы

и .