1.5. Условие равновесия двух сил (вторая аксиома). Принцип присоединения и исключения уравновешенных сил (третья аксиома)

Вторая аксиома устанавливает условие равновесия двух сил.

Две равные между собой силы ( = ), приложенные к абсолютно твердому телу и направленные по одной прямой в противоположные стороны, взаимно уравнове­шиваются (рис.3, а).

Третья аксиома служит основой для преобразования систем сил.

Не нарушая равновесия абсолютно твердого тела, к нему можно приложить или отбросить от него уравно­вешенную систему сил.

Пусть тело (рис. 3, б) находится в состоянии равно­весия. Если к нему приложить несколько взаимно урав­новешенных сил = , = , = , то равно­весие тела не нарушится. Аналогичный эффект получится при отбрасывании этих уравновешенных сил. Системы сил, показанные на рис. 3, а, б, эквивалентны, так как они дают одинаковый эффект– под действием каждой из них тело находится в равновесии.

Из второй аксиомы вытекает следствие, согласно которому всякую силу, действующую на абсолютно твердое тело, можно перенести вдоль линии ее действия в любую точку тела, не нарушив при этом его равновесие.

Действительно, пусть на тело в точке А действует сила (рис. 3, в). В произвольной точке В на линии действия силы приложим две силы и , равные по величине и направленные в противоположные стороны. Равновесие тела в этом случае не нарушится; отбрасыва­ние сил и , как равных и противоположно направленных, также не нарушит равновесия. Таким образом, силу мы заменили равной силой , перенесенной по линии действия из точки А в точку В. Векторы, которые можно переносить по линии их действия, называют скользящими. Как показано выше, сила является скользящим вектором. Необходимо под­черкнуть, что перенос силы по линии ее действия возмо­жен только в том случае, когда тела рассматриваются как абсолютно твердые. При других предпосылках это невозможно.

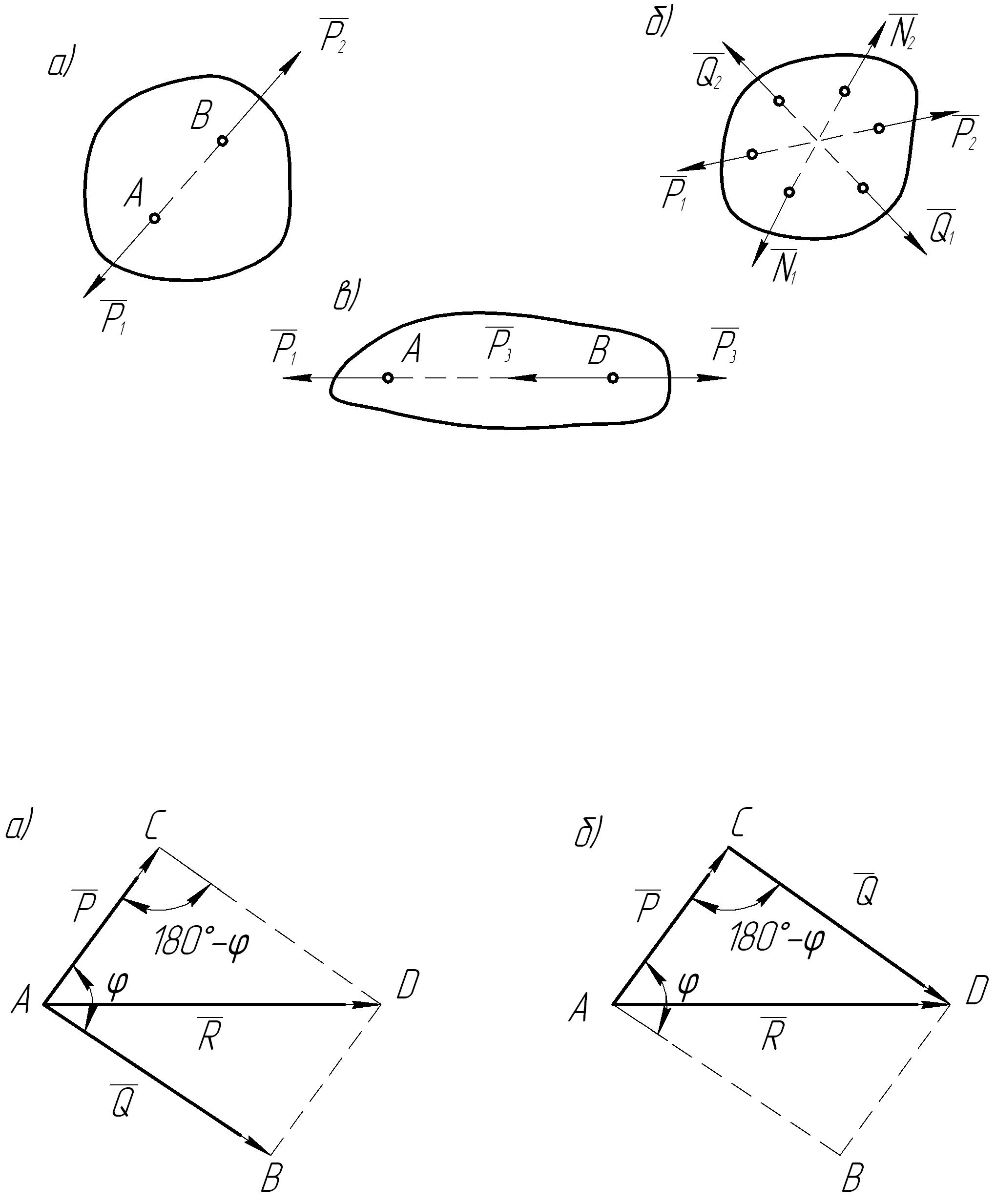
Рис. 3 .Уравновешенные системы сил.

1.6. Правило параллелограмма (четвертая аксиома)

Четвертая аксиома служит основой для сложения сил. Равнодействующая двух сил, приложенных к одной точке, приложена в этой точке и изображается по вели­чине и направлению диагональю параллелограмма, построен­ного на данных силах. Так, равнодействующей двух сил и , приложенных в точке А (рис. 4, а), будет сила , представляющая диагональ параллелограмма ACDB, построенного на векторах заданных сил. Определение рав­нодействующей двух сил по правилу параллелограмма называется векторным, или геометрическим, сложением и выражается векторным равенством

= + .

При графическом определении равнодействующей двух сил вместо правила параллелограмма можно пользоваться правилом треугольника.

Рис. 4.Сложение двух сил.

Из произвольной точки А (рис. 4, б) проводим, сохраняя масштаб и заданное на­правление, вектор первой составляющей силы из его конца проводим вектор, параллельный и равный второй составляющей силе . Замыкающая сторона AD тре­угольника и будет искомой равнодействующей . Ее можно также представить как диагональ параллелограмма ABDC, построенного на заданных силах.