3.4. Аксиомы динамики.

В динамике рассматривается движение материальных точек или тел под действием приложенных сил; устанав­ливается связь между приложенными силами и вызывае­мым ими движением.

Динамика изучает такие системы сил, которые не находятся в состоянии равновесия. Она основывается на ряде вытекающих из опыта аксиом; некоторые из них были рассмотрены ранее в статике.

Напомним содержание первой аксиомы, так называе­мого закона инерции, рассмотренного в статике .

Система сил, приложенная к материальной точке, является уравновешенной, если под ее воздействием точка находится в состоянии относительного покоя или движется равномерно и прямолинейно. Таким образом, первая аксио­ма определяет условия, при которых система сил взаимно уравновешена и, следовательно, эквивалентна нулю.

Однако аксиома имеет еще и другой смысл, на котором следует остановиться подробнее. В случае относительного покоя или равномерного и прямолинейного движения уско­рение материальной точки равно нулю. Поэтому под дей­ствием уравновешенной системы сил или при отсутствии силовых воздействий материальная точка не испытывает ускорений и движется равномерно и прямолинейно.

Когда на точку действует неуравновешенная система сил, точка будет иметь некоторое ускорение. Связь ме­жду действующей на точку силой и ускорением, вызы­ваемым этой силой, устанавливается второй аксиомой ди­намики, которая заключается в следующем:

Ускорение , сообщаемое материальной точке прило­женной к ней силой , имеет направление силы и по величине пропорционально ей (рис. 32, а):

= т ,

где m — коэффициент пропорциональности, связыва­ющий силу с ускорением, появившимся в ре­зультате приложения силы.

Уравнение называется основным уравнением ди­намики в векторной форме. Оно справедливо также и в скалярной форме

Р = та.

Различие между первой и второй формами заключается в том, что векторная форма уравнения учитывает направ­ление векторов силы и ускорения, а скалярная форма учитывает только численные значения этих величин.

Коэффициент т, входящий в основное уравнение ди­намики, имеет очень важное физическое значение. Он представляет собой массу материальной точки.

Если решить уравнение относительно уско­рения, получим

а = .

Из этого уравнения видно, что чем больше масса, тем большая сила потребуется для сообщения телу определен­ного ускорения. Следовательно, масса ха­рактеризует «инертность», или «неподатливость» тела воздействию силы.

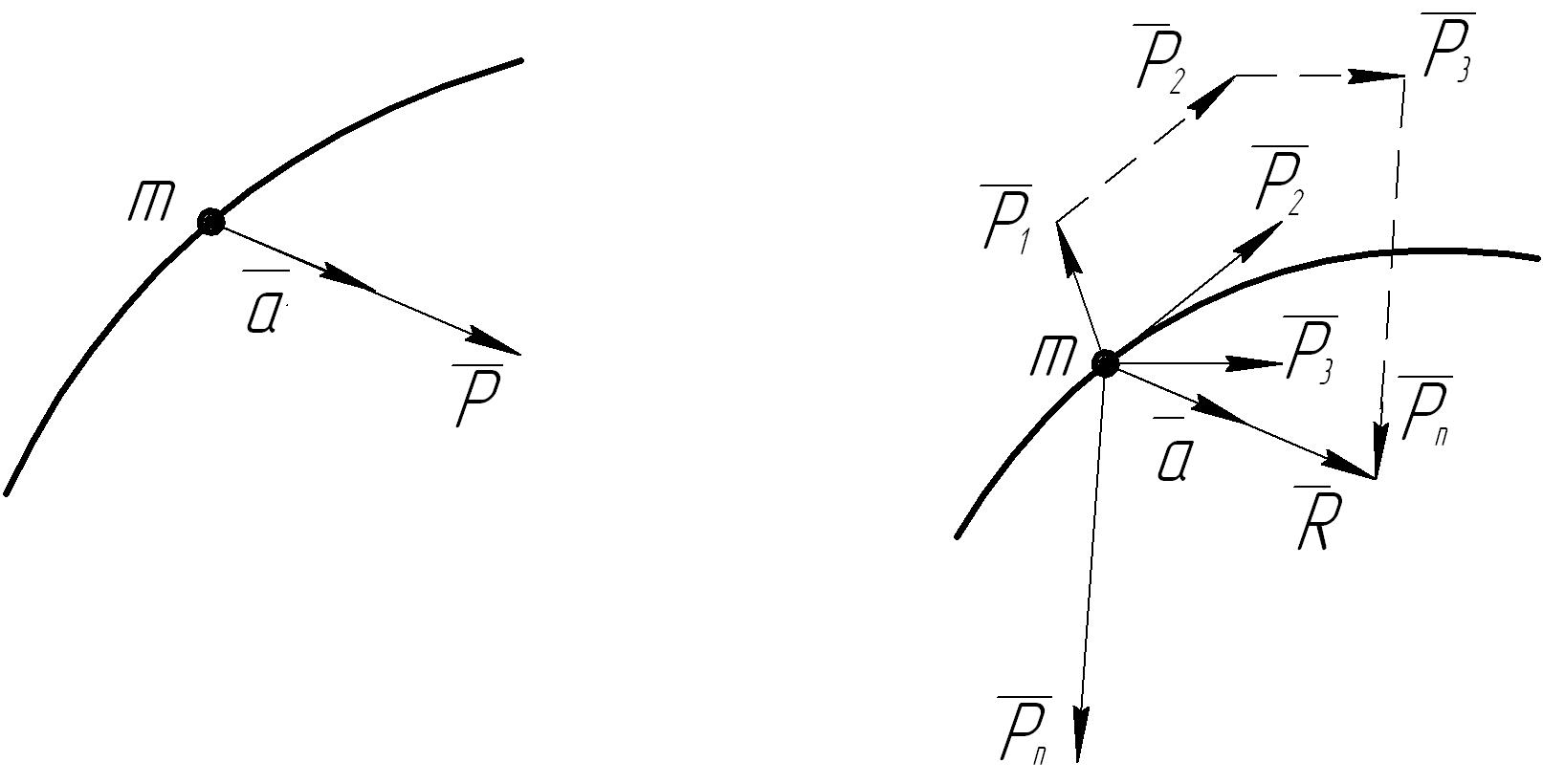
Рис. 32. Векторы силы и ускорения.

Таким образом, масса материальной точки является мерой ее «инертности».

Для вращательного движения тела основное уравнение динамики имеет вид

= I ,

где I – момент инерции тела (мера инертности тела во вращательном движении); ε - угловое ускорение.

Приведем формулировку аксиомы независимости дей­ствия сил.

Если на материальную точку действует несколько сил, то ускорение, получаемое точкой, будет таким же, как при действии одной силы, равной геометрической сумме этих сил (рис. 32, б), т. е.

т = + + + . . .+ = ,

где - равнодей­ствующая системы сил, приложенных к рассматриваемой точке.

Остановимся на последней аксиоме динамики — ак­сиоме взаимодействия, знакомой из статики.

Всякому действию соответствует равное и противо­положно направленное противодействие. Иными словами, силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю и направлены по прямой, соединяющей эти точки, в противоположные стороны.