Глава 3 .

• ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ.

3.1. Поступательное движение твердого тела.

К простейшим движениям тела относятся поступатель­ное движение и вращение вокруг неподвижной оси.

Поступательным называется такое движение твердого тела, при котором всякая прямая, проведенная в этом теле, остается параллельной своему начальному положению.

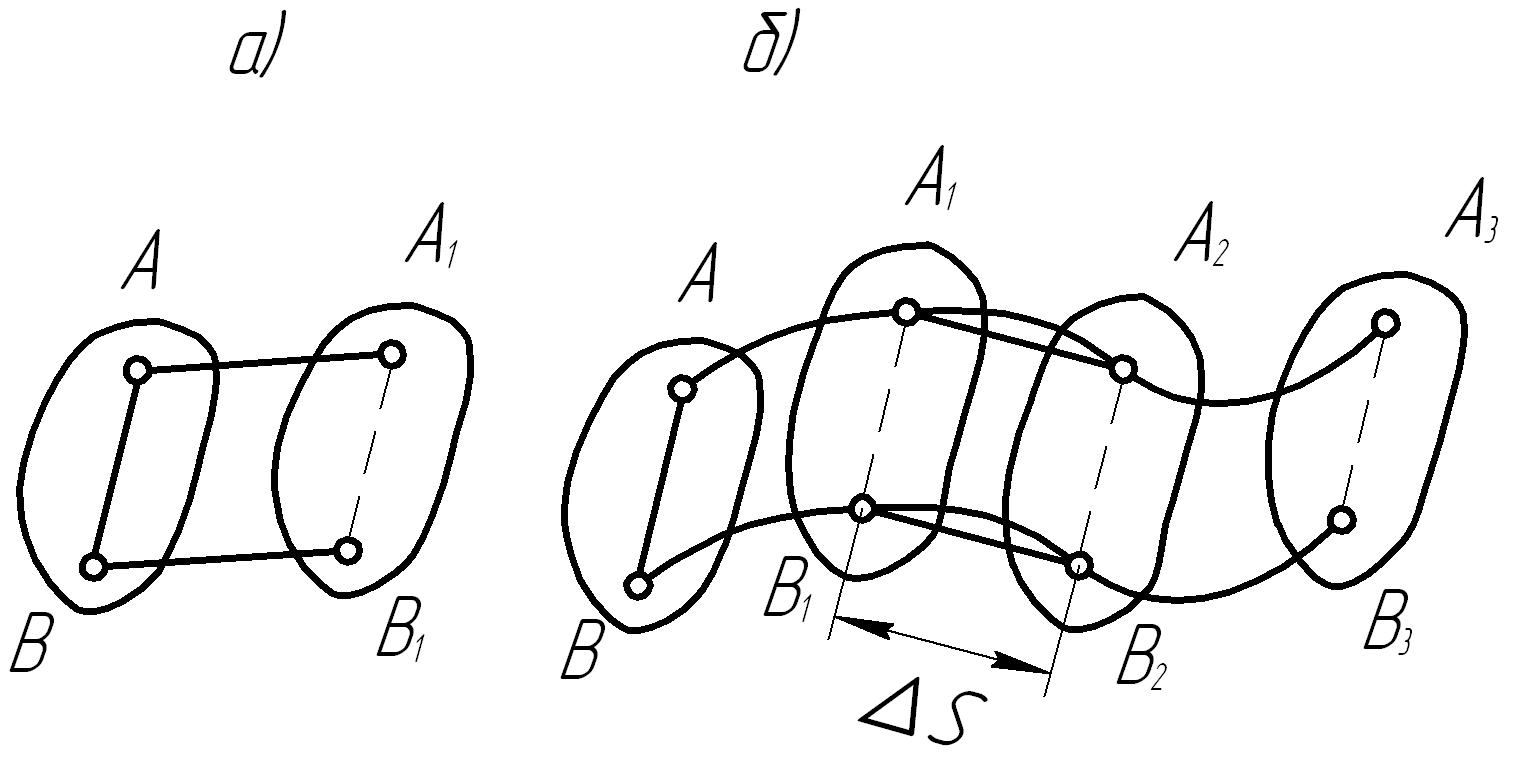
Рис. 29. Поступательное движение тела.

Рассмотрим тело (рис. 29), которое совершает посту­пательное движение. Проведенная в теле прямая АВ во время движения перемещается параллельно своему начальному положению. Рассмотрим перемещение тела за малый промежуток времени Δt.

При этом можно считать, что точки А и В перемещаются по прямолинейным и параллельным прямым. За время Δt они пройдут одинаковые пути Δs. Следовательно, скорости этих точек будут одинаковы по величине

V_A = V_B = V

и направлены в одну сторону, т. е.

= = .

Аналогично доказывается равенство ускорений точек тела при поступательном движении:

= = .

Итак, при поступательном движении тела все его точки описывают одинаковые траектории и в любой момент времени имеют равные по величине и одинаково направлен­ные скорости и ускорения.

Поэтому поступательное движение тела вполне ха­рактеризуется движением одной его точки. Однако поступательное движение может совершать только твердое тело, а не отдельная точка.

Примером поступательного движения служит движе­ние поршня паровой машины, движение вагона на прямом участке пути и т. п.

Поступательное движение может быть прямолинейным и криволинейным. При прямолинейном поступательном движении все точки тела описывают равные и параллель­ные прямые линии (рис. 29, а). При криволинейном по­ступательном движении все точки тела описывают оди­наковые кривые (рис. 29, b).

3.2. Скорости и ускорения точек вращающегося тела.

Точки тела, вращающегося вокруг оси, перемещаются по окружностям (рис. 30, а), радиусы которых r равны расстояниям точек от оси вращения.

Линейная скорость V точки А и угловая скорость ω тела cвязаны между собою линейной зависимостью

V_А= ω r.

Подставив в формулу для линейной скорости точек тела, вращающегося вокруг неподвижной оси, значение n угловой скорости в оборотах в минуту, получим

V_А= r.

Направлена по перпендикуляру к радиусу r в сторону ω (рис.30, а).

В общем случае вектор скорости точки А, вращаясь вокруг точки О, изменяется по величине и направлению. Поэтому у этой точки будет иметь место нормальное ускорение (характеризует изменение по направлению) и тангенциальное ускорение (характеризует изменение по величине). Величина нормального ускорения точки А определится как

= .

Подставляя в это выражение значение скорости V_А= ω r, получаем

= ω² r.

Направлено по радиусу r к центру О вращения.

Касательное ускорение точки определяется из выражения

=ε r,

где ε – угловое ускорение вращающегося тела.

Направлено перпендикулярно r в сторону ε.

Полное ускорение точки при неравномерном вращении вокруг оси (рис. 30, б) геометрически складывается из касательного и нормального ускорений

_А = + .

Рис. 30. Скорости и ускорения точки вращающегося тела.