13. Расчет на прочность балки при сложном сопротив­лении

2.13.1.Построение эпюры продольных сил

Методику построения эпюры N представляем для показанной на рис.28, а схемы нагружения балки с заданной длиной l_АВ (в рассматриваемом примере l_АВ=0,7м. =1000 Н, α=60˚). Направление и значения про­дольных усилий , Р^Г заданы, где =500 Н., Р^Г=РCos α=1000*0,5=500 Н.

Для построения эпюры продольных сил используем метод се­чений (рис.28, б).

Сечение I-I

Равновесие левой части обеспечивается внутренним продоль­ным сжимающим усилием N = = 500 Н.

Сечение ІІ-ІІ

Равновесие левой части обеспечивается продольным усилием

N = - Р^Г =500-500=0

Эти данные использованы для построения эпюры N на рис.28, в.

2.13.2. Построение эпюры изгибающих моментов

Строим схему нагружения балки поперечными усилиями (рис.28,г). Направления и значения усилий , ,Р^В , заданы, где =371 Н, =495 Н, Р^В =РSin α =1000*0,866 =866 Н.

Для построения эпюры изгибающих моментов используем метод сечений.

Сечение І-І О ≤ Z₁ ≤ 0,4 м.

М=- * Z₁;

при Z₁ = О, М = О,

при Z₁ = 0,4 м. М =-371 *0,4 =-148,5 Нм. Сечение П-П 0,4 м. ≤ Z₂ ≤ 0,7 м.

М = - * Z₂ + + ( - )*(Z₂ - 0,225);

при Z₂= 0,4 м., M =-371 *0,4 =-148,5 Нм;

при Z₂= 0,7 м, M =- 371 *0,7 +866*0,3 ≈0.

По результатам расчета строим эпюру М изгибающих мо­ментов (рис.28,д).

2.13.3. Определение геометрических характеристик сечения балки, расчет на прочность

Для прямоугольного сечения балки с размерами h=22 мм, b=14 мм находим.

• Площадь поперечного сечения

F = b*h=14*22=308 мм².

• Момент сопротивления сечения

W_X = = =1129 мм³.

Анализ эпюр продольных сил и изгибающих моментов (рис.28в; 28д) показывает, что опасным является сечение, про­ходящее через точку S балки. В этом сечении име­ют место наибольшая продольная сила N_MAX = = 500 Н. и максимальный изгибающий момент M_MAX =–148,5 Н^.м. Балка в отмеченном сечении испытывает совместное действие изгиба и сжатия. Для определения суммарных напряжений ис­пользуем принцип независимости действия сил.

• Напряжения в опасном сечении от сжимающих усилий

σ_С = = 1,62 МПа.

• Напряжения в опасном сечении от изгиба

_{σИ = = 131,5 МПа.}

• Суммарные напряжения в сжатых волокнах

σ = σ_С + _{σИ = 1,62 + 131,5 ≈133 МПа.}

Полагаем, что балка изготовлен из стали Ст.З, для которой допускаемое напряжение при изгибе [σ] = 150 _МПа . Таким образом, в рассматриваемом случае условие прочности балки при сопротивлении на изгиб со сжатием

σ ≤ [σ], 133 < 150

выполняется.

• Коэффициент запаса прочности балки при сложном сопротивлении n = = 1,13

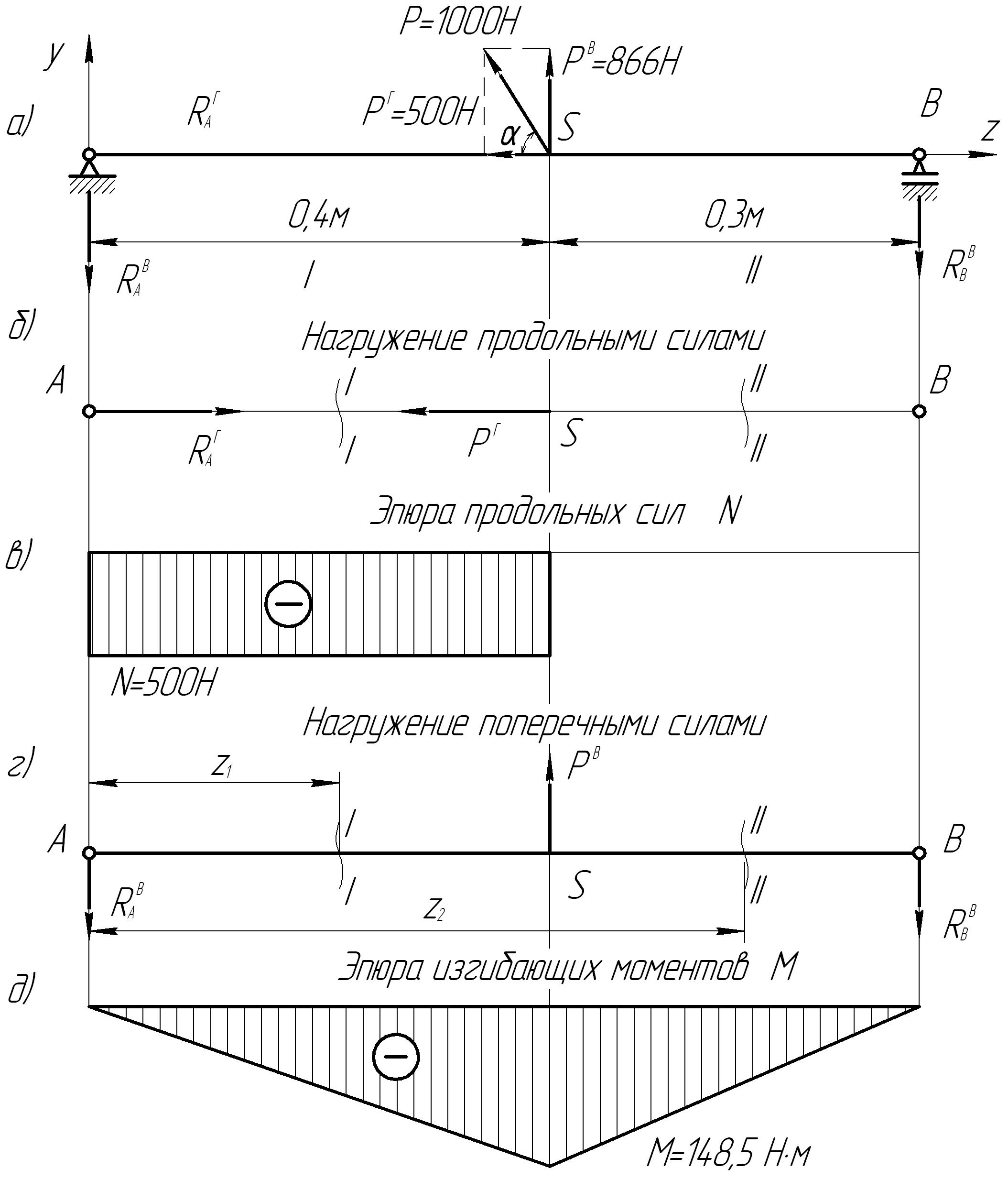
Рис28 Эпюры продольных сил и изгибающих моментов.

• Если при расчетах получили σ >[σ], n < 1, необходимо увеличить геометрические размеры сечения и пов­торить расчет, обеспечив выполнение усло­вия прочности. Последнее можно также обеспечить, приняв в качестве материала балки сталь с более высоким допуска­емым напряжением при изгибе .