2.11. Продольный изгиб.

Рассматривая деформацию сжатия, мы отмечали, что она воз­никает при действии на брус сил, направленных по его продольной оси навстречу друг другу, и что при этом поперечные размеры бруса мало отличаются от его продольных размеров.

Если поперечные размеры бруса будут во много раз меньше его длины (такой брус называют стержнем), то может возникнуть иное напряженное состояние. Вначале, когда силы невелики, стержень действительно подвергается сжатию и его ось будет оставаться прямолинейной. Однако, увеличивая силу, можно подойти к такому ее значению, которое выведет стер­жень из устойчивого положения и его ось станет криволинейной (рис. 26). Естественно, что работоспособность детали при этом будет нарушена. Деформация стержня, яв­ляющаяся следствием потери его устойчиво­сти под действием сжимающих сил, называ­ется продольным изгибом. Сила, которая соответствует моменту перехода стержня из устойчивого положения в неустойчивое, на­зывается критической силой, а напряжение сжатия, соответствующее этой критической силе,— критическим напряжением.

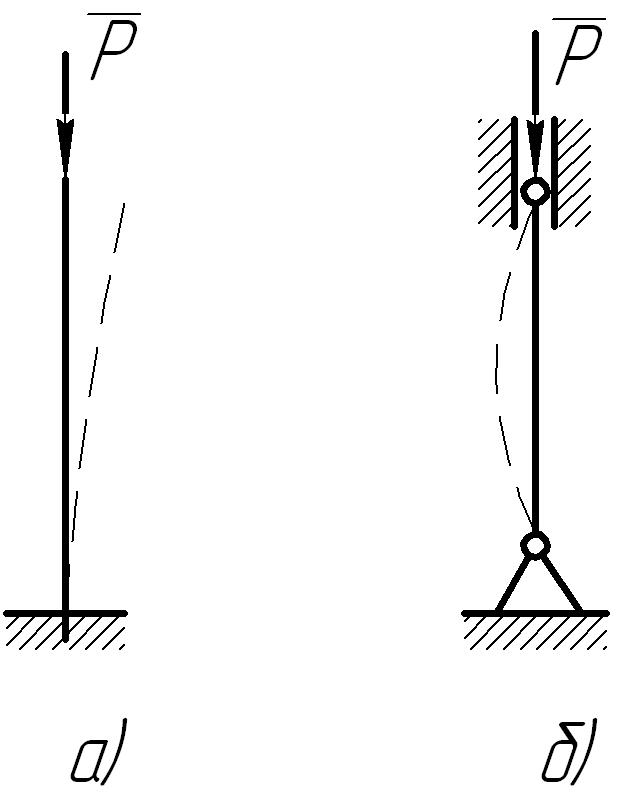
Рис. 26 Продольный изгиб стержней жестко защемленного (а) и с шарнирными опорами (б).

Практика показывает, что это напряже­ние меньше обычного предельно опасного напряжения, ориентируясь на которое, вы­бирают допускаемые напряжения при сжа­тии. Поэтому, чтобы расчет на прочность при сжатии одновременно гарантировал устойчивость, допускаемые напряжения на сжатие при таком нагружении стержней снижают­ся в зависимости от соотношения длины и поперечных размеров стержня и от способа закрепления его концов. Например, при прочих равных условиях стер­жень, закрепленный, как показано на рис. 26, а, менее устойчив, чем стержень, показанный на рис. 26, б.

2.12. Сложное сопротивление

Мы рассматривали случаи простых деформаций: растяжение, сжатие, сдвиг, кручение, поперечный и продольный изгибы. Одна­ко некоторые детали могут испытывать одновременно несколько простых деформаций, т. е. сложное сопротивление. Наиболее час­то встречаются следующие комбинации простых деформаций: рас­тяжение (сжатие) с изгибом и изгиб с кручением.

Если брус нагружен так, как показано на рис. 27, а, то это обычная деформация растяжения. Если брус нагружен так , как показано на рис.27, б (теперь это балка), то это обычная деформация поперечного изгиба. А если нагружение будет таким, как показано на рис. 27, в? Определить вид деформации в этом случае нетрудно, если раз­ложить заданную силу Р на две составляющие —P₁ и Р₂ (рис.27, г).Составляющие находятся как проекции силы Р на координатные оси. Тогда ясно, что нагружение аналогично сумме двух первых нагружений (рис.27, а, б), а значит, и напряженное состояние будет соответствовать одновременному появлению напряжений растяжения и напряжений изгиба. Проанализируем действие силы Р₁.

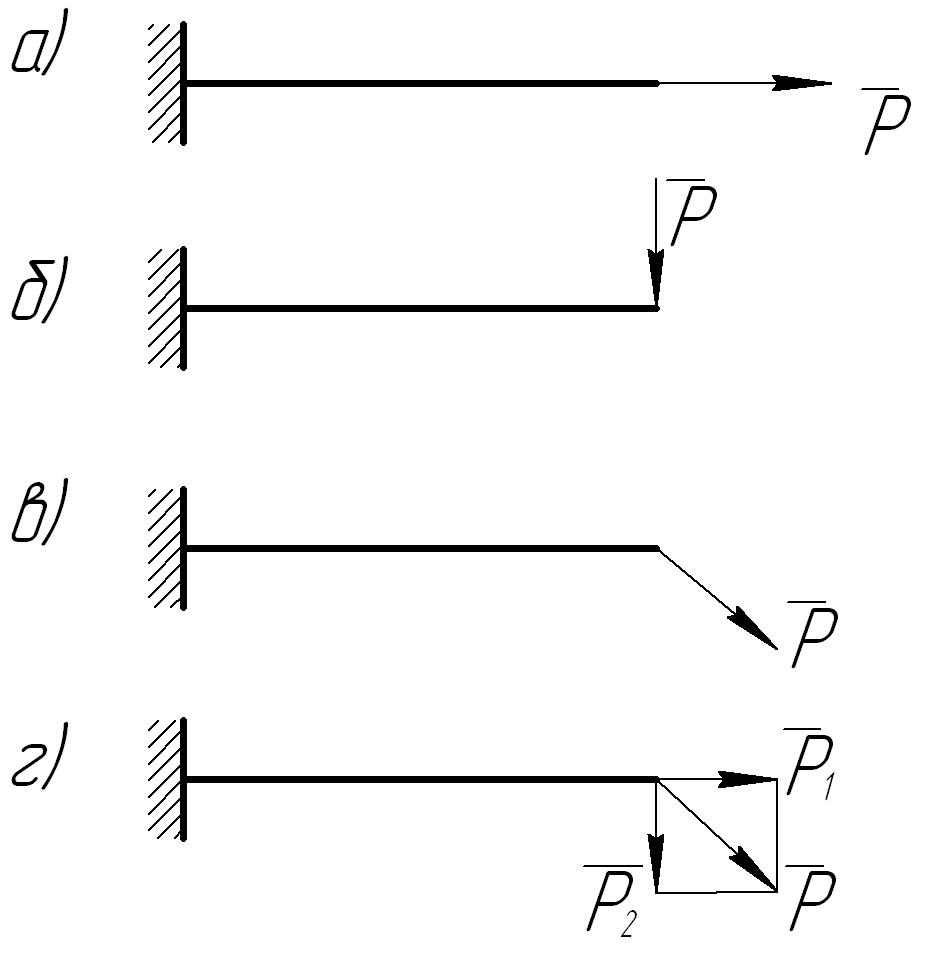
Рис. 27 Различные виды деформаций: а- растяжение; б- поперечный изгиб; в -сложная

деформация; г -сложная деформация как сумма двух простых деформаций.

При деформации растяжения все сечения по длине бруса и все точки в сечениях равноопасны. Равнодействующая внутренних сил N=P₁. Величина напряжения

σ_р = ,

где F — площадь поперечного сечения бруса.

Проанализируем действие силы Р₂. Здесь наиболее опасно сечение в заделке (там наибольший изгибающий момент М_И=Р₂l) и в этом сечении наиболее опасны точки, дальше всего расположен­ные от нейтральной оси. Напряжение в этих точках

σ_{И max} = ,

где Р₂l — изгибающий момент в заделке, W — осевой момент со­противления сечения изгибу.

Нормальные напряжения σ_р и σ_{И max} можно складывать алгеб­раически (они направлены по одной прямой). Очевидно, что в итоге наиболее опасным будет сечение в заделке, и в этом сечении наиболее опасными будут те точки, в которых напряжения сумми­руются, т. е. там, где у них будет одинаковый знак:

σ_сум = .