1.14. Приведение силы к точке

В начале Х1Х века Л. Пуансо доказал теорему о параллельном переносе силы в любую заданную или выбранную точку.

Пусть дана сила , приложенная к точке А твердого тела, и ее требуется перенести в точку О (рис. 16, а). Приложим к телу в точке 0 (рис. 16,6) уравновешенную систему сил ,^{′ ′′}, параллельных и равных ей по модулю (т. е. P' = P" = P). Теперь кроме силы ^′′, приложенной к точке О, образовалась пара сил ( , ^′) с моментом М=P h. но так как и момент данной силы относительно точки О равен М₀( )=P h, то М= М_о( ).

Таким образом, всякую силу , приложенную к телу в точке А, можно переносить параллельно линии действия в любую точку О, присоединив пару сил, момент которой равен моменту данной силы отно­сительно новой точки ее приложения.

Операция такого переноса силы называется при­ведением силы к точке, а появляющаяся при этом пара ( , ^′) с моментом М= М_о( ) называется присоединенной парой (рис. 16, в).

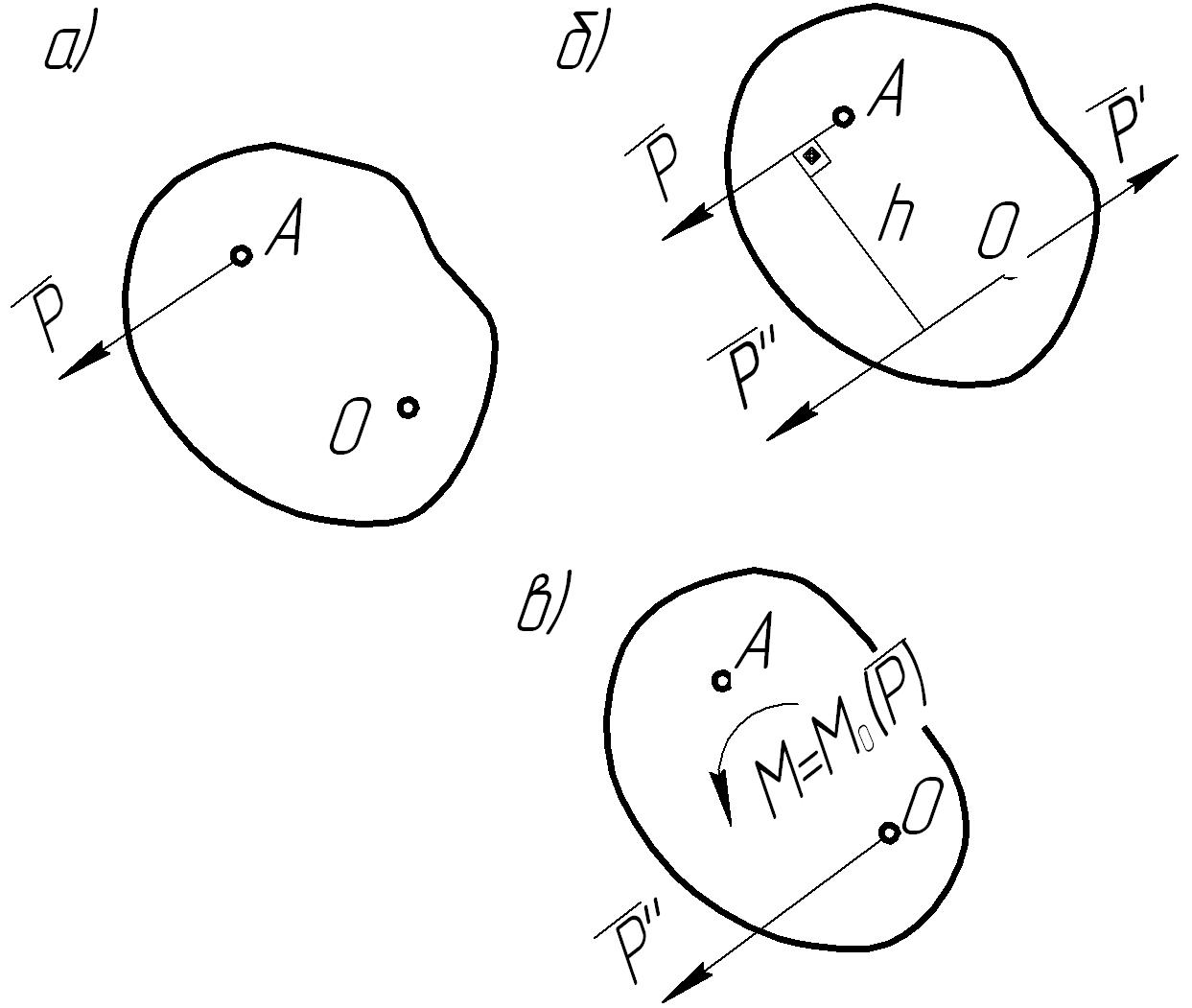
Рис. 16. Приведение силы в точку О.

Изложенный метод приведения одной силы к данной точке можно применить к какому угодно числу сил, которые приводятся в одну точку. Сходящиеся в этой точке силы заменяем одной силой ( ), которая является геометрической суммой этих сил и называется главным вектором системы сил. По аналогии с главным вектором получаем главный момент системы (М_г) относительно точки приведения, складывая алгебраически моменты присоединенных пар.

Таким образом, плоская система сил может быть заменена эквивалентной ей системой, состоящей из одной силы и одной пары сил. Очевиден факт, что система сил находится в равновесии, когда главный вектор системы сил ( )и главный момент системы (М_г) равны нулю. Это условие называется условием равновесия плоской системы сил.

Глава 2. Основы сопротивления материалов

2.1. Деформация тел под действием внешних сил

На все детали машин и сооружений во время их работы дейст­вуют различные внешние силы. При определении величины и на­правления таких сил, приложенных к телам, находящимся в рав­новесии, обычно делается допущение, что все тела абсолютно твердые, т. е. недеформируемые. Об этом говорилось выше в разделе «СТАТИКА».

В действительности тела под действием приложенных к ним сил в той или иной степе­ни меняют свою форму и размеры, т. е. де­формируются. Различают упругую и остаточную деформации. Деформация, полностью ис­чезающая после прекращения действия внеш­них сил, называется упругой. Если после сня­тия нагрузки тело не восстанавливает прежней формы, то говорят об остаточной (пластиче­ской деформации).

Характер деформации (упругая или оста­точная) зависит от величины силы, действую­щей на тело, размеров тела и механических свойств его материала Мы будем знакомиться с деформацией тел наиболее простой формы. Таким телом явля­ется прямолинейный брус — тело с прямой осью, у которого длина больше поперечных размеров. Для упрощения расчетов мы будем считать, что сам брус не имеет массы. . В зависимости от направ­ления действия сил, приложенных к телу, мо­гут возникать различные виды деформаций: растяжение, сжатие, сдвиг, кручение, изгиб.

Деформация растяжения или сжатия воз­никает в том случае, когда внешние силы на­правлены по одной прямой (вдоль оси бруса) в разные стороны (рис. 17, а, б). Если на брус действуют внешние силы, стремящиеся сдви­нуть одну

часть его относительно другой, то возникает деформация сдвига (рис. 17, в).

Если брус находится под действием нагрузок, создающих противоположные пары сил в плоскостях, перпендикулярных продольной оси бруса, то появляется деформация кручения (рис. 17, г). И, наконец, две равные пары сил разного знака создают деформацию изгиба (рис. 17, д).

Рис. 17. Виды дефор­маций:

а — растяжение ; б—сжатие; в — сдвиг; г —кручение; д — изгиб.

Чтобы любая деталь машины была работоспособна, т. е. мог­ла работать безопасно и быть достаточно долговечной, она не только не должна разрушаться от действия на нее рабочих усилий, но и деформации, возникающие в ней при этом, должны быть весьма малыми и обя­зательно упругими. Определить минимальные размеры детали, необходимые для обеспечения ее работоспособности в соответствии с действующими на нее нагрузками и свойствами материала, из которого эта деталь изготовлена, можно методами, изучаемыми в разделе технической механики– «Сопротивление материалов».