- •Часть 4
- •Глава 9. Основные понятия дискретной математики
- •Элементы комбинаторики Понятие соединения
- •Перестановки
- •Размещения
- •Сочетания
- •Элементы математической логики Понятие высказывания
- •Сложное высказывание
- •Логические операции
- •Отрицание высказывания
- •Конъюнкция высказываний
- •Дизъюнкция высказываний
- •Вопросы для самоконтроля:
- •Упражнения для самостоятельной работы
- •Глава 10. Элементы теории вероятностей Понятие события
- •Определение вероятности
- •Свойства вероятности
- •Правило сложения вероятностей
- •Правило: Вероятность того, что произойдёт какое-либо из рассматриваемых событий, равна сумме вероятностей этих событий: Правило умножения вероятностей
- •Правило: Вероятность того, что произойдут сразу несколько из рассматриваемых событий, равна произведению вероятностей этих событий: Связь между частотой появления события и его вероятностью
- •Случайные величины: дискретные и непрерывные
- •Закон распределения дискретной случайной величины
- •Числовые характеристики дискретной случайной величины
- •Вопросы для самоконтроля:
- •Упражнения для самостоятельной работы
Случайные величины: дискретные и непрерывные
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.
Например, число студентов на лекции, число больных студентов, число студентов, обратившихся к медицинской сестре за помощью.
Случайные величины обозначают прописными буквами латинского алфавита: X, Y, Z, …, а их значения соответствующими строчными буквами: x, y, z, … вычислительной системе случайные величины можно разделить на две группы: дискретные и непрерывные.
Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отделённые друг от друга значения, которые можно перенумеровать.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Например, количество новорождённых (смертей, свадеб, разводов…) за каждую неделю, месяц, год…
Непрерывной случайной величиной (в широком смысле слова) называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.
Число возможных значений непрерывной случайной величины бесконечно. Например, возраст человека, температура воздуха в течение дня, недели, месяца, года…
Закон распределения дискретной случайной величины
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
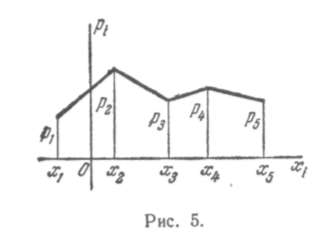
Закон распределения может иметь разные формы: для дискретной случайной величины он может быть представлен в виде таблицы или графика.
Рядом распределения дискретной случайной величины X называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn, с соответствующими им вероятностями p1 , p2, ..., рn:
Х |
x1 |
x2 |
… |
xi |
… |
xn |
|
Р |
p1 |
p2 |
… |
pi |
… |
pn |
|
|
|||||||
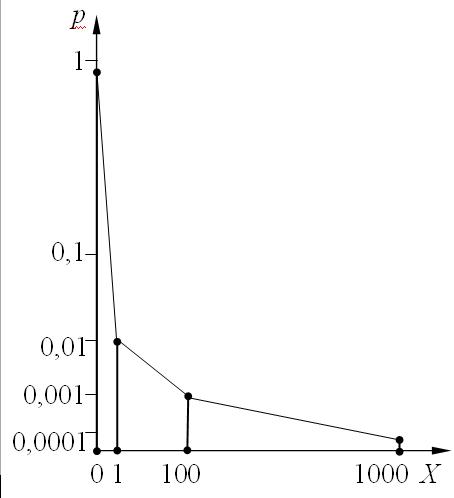
Решение: составим ряд распределения случайной величины: |
|
||||
Х |
1000 |
100 |
1 |
0 |
|
Р |
0,0001 |
0,001 |
0,01 |
0,9889 |
|
Возможные значения Х: х1=1000, х2=100, х3=1, х4=0.
Соответствующие
вероятности:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Числовые характеристики дискретной случайной величины
Математическим ожиданием дискретной случайной величины называют среднее арифметическое её значение.
![]()
Если случайная величина задана рядом распределения, то:
![]()
Дисперсией дискретной случайной величины называют среднее арифметическое квадратов отклонений значений случайной величины от математического ожидания.
![]()
Если случайная величина задана рядом распределения, то:
![]()