Правило: Вероятность того, что произойдёт какое-либо из рассматриваемых событий, равна сумме вероятностей этих событий: Правило умножения вероятностей

9. Произведением двух или нескольких событий называется событие, состоящее в появлении всех этих событий.

10. Два кубика подбрасываются одновременно. Какова вероятность того, что одновременно выпадут две четвёрки?

Решение: Обозначим: событие А – выпадение четвёрки. В этом случае mAА = 1, n = 66 = =36. Тогда вероятность события AA:		1	2	3	4	5	6
	1	1 и 1	2 и 1	3 и 1	4 и 1	5 и 1	6 и 1
	2	1 и 2	2 и 2	3 и 2	4 и 2	5 и 2	6 и 2
	3	1 и 3	2 и 3	3 и 3	4 и 3	5 и 3	6 и 3
	4	1 и 4	2 и 4	3 и 4	4 и 4	5 и 4	6 и 4
	5	1 и 5	2 и 5	3 и 5	4 и 5	5 и 5	6 и 5
	6	1 и 6	2 и 6	3 и 6	4 и 6	5 и 6	6 и 6

Правило: Вероятность того, что произойдут сразу несколько из рассматриваемых событий, равна произведению вероятностей этих событий: Связь между частотой появления события и его вероятностью

Итак, из классического определения вероятности следует, что вероятность выпадения шестёр­ки при бросании игральной кости равна 1/6. Значит ли это, что при шести выбрасываниях ку­бика шестёрка выпадет ровно 1 раз? – нет! В реальности мы можем получить от 0 до 6 выпадений «6» при проведении 6 опытов с выбрасыванием игральной кости. Чтобы опреде­лить вероятность практически, нужно проделать большое количество опытов и проследить, как часто выпадает шестёрка. Для этого нужно выполнить несколько серий опытов по 100 (например) бросаний кубика в каждой. 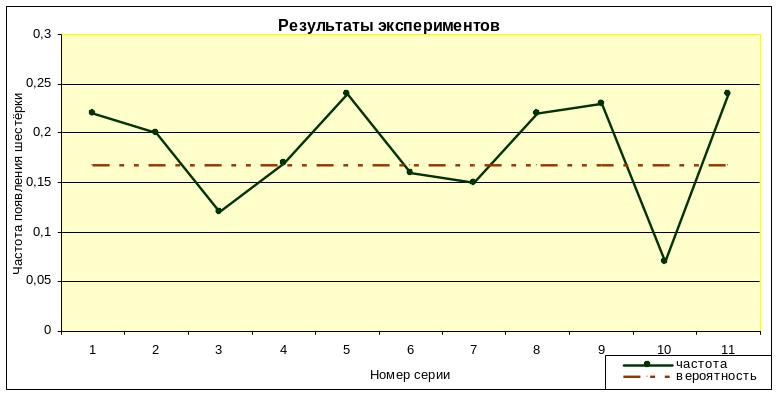В результате нетрудно убедиться, что частота случайного события = «появление шестёрки» в каждой серии колеблется около классической вероятности данного события (см. график).

номер серии	1	2	3	4	5	6	7	8	9	10	11
частота	0,22	0,2	0,12	0,17	0,24	0,16	0,15	0,22	0,23	0,07	0,24
вероятность	1/6 = 0,167

Если производится n независимых опытов в одинаковых условиях, причём в каждом из них с вероятностью (частотой) p появляется событие A, то вероятность P_m,n того, что событие A произойдёт в этих n опытах ровно m раз, выражается формулой: , где q=1–p.

При увеличении числа испытаний отклонение частоты появления события от классической вероятности события уменьшается, стремясь к 0 при n. Это утверждение носит название Закона Больших Чисел.