Глава 10. Элементы теории вероятностей Понятие события

Различные явления и процессы происходят в окружающем мире. Они, как правило, являются следствиями предыдущих или причинами следующих.

1. Событием называется всякий факт, который в результате опыта может произойти или не произойти.

Будем обозначать события первыми прописными буквами латинского алфавита.

Все события можно разделить на две группы. Одни из них являются однозначными исходами опыта, предсказать которые можно абсолютно точно. Например, нажатие на кнопку выключателя (опыт, причина) повлечёт однозначный исход – свет в помещении погаснет (событие, следствие).

2. Событие, являющееся однозначным исходом опыта, называется строго детерминированным событием (от лат. «determinare» – определять).

Другие опыты могут вызвать различные варианты исхода, точно предсказать который невозможно, можно лишь попытаться его угадать. Например, подбрасывание кубика (игральной кости) повлечёт один из 6 исходов: выпадет 1, 2, 3, 4, 5 или 6.

3. Событие, являющееся одним из нескольких исходов опыта, называется случайным событием.

Определение вероятности

4. Вероятностью события называется численная мера степени объективной возможности этого события.

5. Если несколько исходов одного опыта имеют одинаковые шансы, то они называются равновозможными.

6. Несколько событий в данном опыте называются несовместными, если никакие два из них не могут появиться вместе.

Среди всех равновозможных событий (исходов) выделим благоприятные (желаемые). Вероятность P_A события A определяется отношением числа m_A благоприятных исходов к общему числу n всех равновозможных исходов:

7. Определить вероятность выпадения нечётного числа очков при бросании кубика. Обозначим: событие A – выпадение на грани кубика нечётного числа очков. В этом случае m_A = 3, n = 6. Тогда вероятность данного события

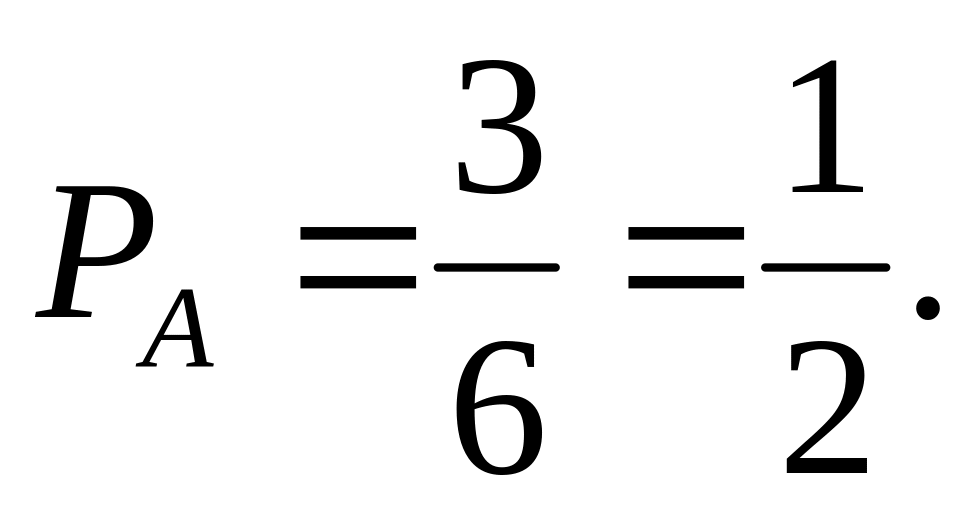
7. Несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них, называются полной группой событий.

Свойства вероятности

1. Если m_A = n, то P_A = 1: событие А – достоверное событие (реализуется при каждом исходе).

2. Если m_A = 0, то P_A = 0: событие А – невозможное событие (не реализуется вообще).

3. Вероятность любого случайного события A заключена между нулём и единицей: 0 <P_A < 1.

4. Сумма вероятностей случайных событий, составляющих полную группу событий, равна единице: P = P_A + P_B + P_C + … = 1.

8. В мешке 23 шара: 10 жёлтых, 7 синих и 6 зелёных. Какова вероятность того, что первый извлечённый наугад шар окажется жёлтым? Синим? Зелёным? Чёрным? Какова полная вероятность событий в данном опыте?

Решение: Обозначим: событие А – извлечение жёлтого шара,

событие В – извлечение синего шара,

событие С – извлечение зелёного шара,

событие D – извлечение чёрного шара.

В этом случае m_A = 10, m_В = 7, m_С = 6, m_D = 0, n = 23.

Тогда вероятности рассматриваемых событий: – событие D – невозможное.

Полная вероятность рассматриваемых событий:

Правило сложения вероятностей

8. Суммой двух или нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

9. В мешке 23 шара: 10 жёлтых, 7 синих и 6 зелёных. Какова вероятность того, что первый извлечённый наугад шар окажется жёлтым или синим?

Решение: Обозначим: событие А+В – извлечение жёлтого или синего шара.

В этом случае m_A+В = 10+7= 17, n = 23. Тогда вероятность события А+В: