Дизъюнкция высказываний

Составим сложное высказывание из двух простых при помощи союза «или».

A: «Сергей– северодвинец»;

B: «Сергей– студент медицинского колледжа».

Тогда A или B: «Сергей – северодвинец или студент медицинского колледжа».

Операция объединения высказываний при помощи союза «или» называется дизъюнкцией вы­сказываний (от латинского «disjunctio» – разобщение, различие) и обозначается «AB».

Дизъюнкцией высказываний A и B называется такое высказывание AB, ко­торое истинно в том случае, если истинно хотя бы одно из данных высказываний A или B. Таблица истинности конъюнкции высказываний «A или B» в соответствии с определением выглядит так:	A	B	AB
	0	0	0
	0	1	1
	1	0	1
	1	1	1

A	B	C	AB	C	ABC	Составим таблицу значений для сложного высказывания ABC. Логические задачи Сложные логические задачи легко ре­шаются с помощью таблицы истин­ности. Например: Три брата – Иван, Дмитрий и Сергей – преподают различные дисциплины –
0	0	0	0	0	0
0	0	1	0	1	0
0	1	0	1	0	0
0	1	1	1	1	1
1	0	0	1	0	0
1	0	1	1	1	1
1	1	0	1	0	0
1	1	1	1	1	1

химию, биологию и историю – в университетах Москвы, Архангельска, Санкт-Петербурга. Иван – не москвич. Дмитрий – не биолог и не архангелогородец. Москвич – не историк. Архангелогородец – химик. Что и в каком городе преподаёт Сергей?

Москва	Архангельск	Санкт-Петербург		биолог	историк	химик
0			Иван
	0		Дмитрий	0		0
			Сергей

Вопросы для самоконтроля:

1. Перестановки и формула их вычисления;

2. Размещения и формула их вычисления;

3. Сочетания и формула их вычисления;

4. Понятие высказывания. Сложное высказывание.

5. Логические операции. Отрицание высказывания: таблица истинности.

6. Конъюнкция высказываний: таблица истинности.

7. Дизъюнкция высказываний: таблица истинности.

Упражнения для самостоятельной работы

1. Вычислите число следующих соединений:

   ;

   ;

   ;

   ;

   .

   .

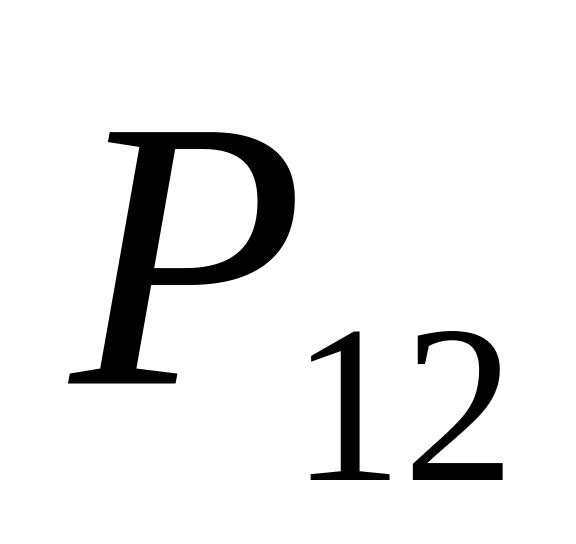2. Выберите среди приведённых ниже предложений высказывания и определите их истинность:

   Предложение	Является ли высказыванием?	Значение A
   10 часов;
   Москва – столица России;
   2,01 – целое число.

3. Составьте отрицания приведённых ниже высказываний и определите их истинность:

   A	A	ЗначениеA
   17 – составное число;
   y = sinx – тригонометрическая функция;
   …

4. Составьте высказывания приведённых ниже отрицаний и определите их истинность:

A	A	Значение A
;
…

Используя высказывания и из строк 4.1. и 4.2., составьте дизъюнкцию и конъюнкцию двух высказываний и определите их истинность.

5. Составьте таблицы их истинности приведённых ниже сложных высказываний и:

   1. (AB) C;

   2. (AB)C;

   3. (AB)(CD).

6. Решите логическую задачу с помощью таблицы истинности: Любимые ученики Анны Ивановны – Андрей, Пётр и Василий – учитель, врач и инженер. Андрей – не инженер. Василий – не врач и не Алексеевич. Николаевич – не инженер. Фёдорович – врач. Определите отчества и профессии учеников Анны Ивановны.