
- •Часть 4
- •Глава 9. Основные понятия дискретной математики
- •Элементы комбинаторики Понятие соединения
- •Перестановки
- •Размещения
- •Сочетания
- •Элементы математической логики Понятие высказывания
- •Сложное высказывание
- •Логические операции
- •Отрицание высказывания
- •Конъюнкция высказываний
- •Дизъюнкция высказываний
- •Вопросы для самоконтроля:
- •Упражнения для самостоятельной работы
- •Глава 10. Элементы теории вероятностей Понятие события
- •Определение вероятности
- •Свойства вероятности
- •Правило сложения вероятностей
- •Правило: Вероятность того, что произойдёт какое-либо из рассматриваемых событий, равна сумме вероятностей этих событий: Правило умножения вероятностей
- •Правило: Вероятность того, что произойдут сразу несколько из рассматриваемых событий, равна произведению вероятностей этих событий: Связь между частотой появления события и его вероятностью
- •Случайные величины: дискретные и непрерывные
- •Закон распределения дискретной случайной величины
- •Числовые характеристики дискретной случайной величины
- •Вопросы для самоконтроля:
- •Упражнения для самостоятельной работы
Филиал ГАОУ СПО АО
«Архангельский медицинский колледж»
в г. Северодвинске
Н.С. Антипова
МАТЕМАТИКА
для специальностей
среднего медицинского образования
(базовый уровень)
Учебно-методическое пособие
Часть 4
Северодвинск, 2013
Глава 9. Основные понятия дискретной математики
Разделы математики «Математическая логика» и «Теория вероятностей» содержат базовые понятия для изучения «Математической статистики» – прикладной науки, лежащей в основе оценки состояния, планирования и прогнозирования направлений развития любой отрасли народного хозяйства. В частности, санитарная статистика играет важнейшую роль в оценке состояния здоровья населения, деятельности медицинских учреждений, планирования и прогнозирования деятельности различных служб на современном этапе развития отечественного здравоохранения.
Кроме того, современные информационные технологии используются на всех этапах медицинского обследования пациента: работа с банком данных медицинских карт, диагностика (томографические исследования, УЗИ, и т.п.), составление разнообразной текстовой документации (направления, результаты обследования, карты амбулаторного наблюдения и т.д.). А работа любого компьютера построена на принципах математической логики.
Хочешь понять логику компьютера – изучи математическую логику. Ей посвящён данный раздел.
Элементы комбинаторики Понятие соединения
Общим именем соединений принято называть следующие три типа комбинаций, составляемых из некоторого числа различных между собой элементов: перестановки, размещения и сочетания.
Перестановки
Рассмотрим множество различных элементов а1, а2, …, аn. Будем переставлять эти элементы местами.
Перестановкой называется каждая комбинация из n элементов (в том числе и первоначальная), получаемая при перемене порядка элементов в последовательности с неизменным количеством элементов.
Число
всех различных перестановок из
n
элементов
обозначается Pn
и определяется по формуле:
![]()
n! – называется факториáлом числа n, читается: «n-факториáл».
Факториáл числа равен произведению последовательных натуральных чисел от 1 до n, причём принято считать 0!=1.
а)
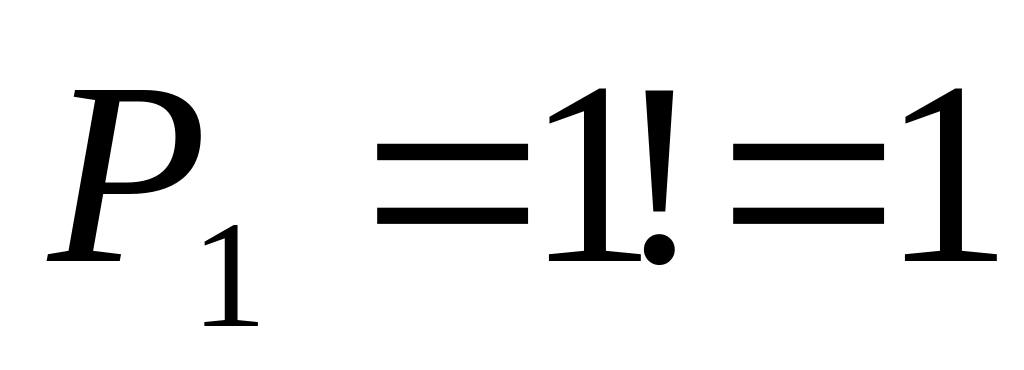 ;
б)
;
б)
 ;
в)
;
в)
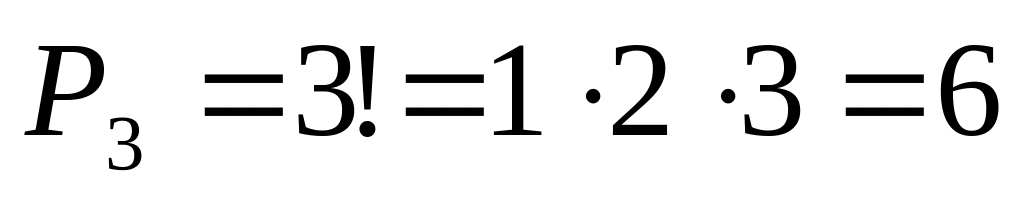 ;
;
г)
![]() ;
д)
;
д)
![]() .
.
Проверим: составим перестановки из 3 элементов a,b,c: abc, acb, bac, bca, cab, cba – всего 6 перестановок.
Размещения
Составим из n элементов группы по m элементов в каждой, располагая взятые элементы в различном порядке.
Размещением из n элементов по m называется каждая комбинация, получаемая при выборе из n элементов групп по m элементов, отличающихся друг от друга не только элементами, входящими в состав группы, но и последовательностями их расположения в группе.
составим размещения из 3 элементов a,b,c по 2: ab, ba, ac, ca, bc, cb – всего 6 размещений из 3 по 2.
Число
всех различных размещений из
n
элементов по
m обозначается
![]() и
определяется по формуле:
и
определяется по формуле:
![]() .
.
Вычислим
по формуле
![]() .
.
а)
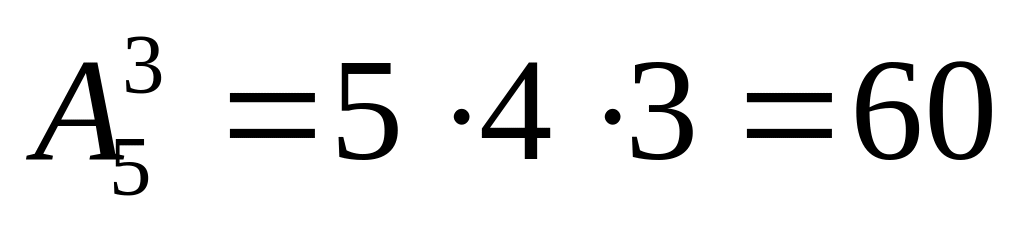 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Сочетания
Составим из n элементов группы по m элементов в каждой, не обращая внимания на порядок их расположения.
Сочетанием из n элементов по m называется каждая комбинация, получаемая при выборе из n элементов групп по m элементов, отличающихся друг от друга только составами элементов.
составим сочетания из 3 элементов a,b,c по 2: ab, ac, bc – всего 3 сочетания из 3 по 2.
Число
всех различных сочетаний из
n
элементов по
m обозначается
![]() и
определяется по формуле:
и
определяется по формуле:
![]() .
Вычислим по формуле
.
Вычислим по формуле
![]() .
.
