Тема 11.
Окружности, связанные с треугольником и четырехугольником.
Подготовительные задачи.
Задача 1.
Боковая сторона равнобедренного треугольника равна 2, угол при вершине равен .
Н
айдите
диаметр описанной окружности.
Решение.
Радиус окружности
Диаметр описанной
окружности
Ответ: 4.
Задача 2.
Под каким углом видна из точек окружности хорда, равна радиусу?
Р
ешение.
Центральный угол
Угол, под которым видна хорда, зависит от расположения точки
Точка расположена на большей дуге окружности
Вписанный угол равен половине центрального угла
Точка расположена на меньшей дуге окружности
Сумма противоположных углов четырехугольника равна
Ответ:
Задача 3.
В равнобедренном
треугольнике
,
проведена высота
.
.
Радиус окружности,
проходящий через точки
,
равен
.
Н
айдите
площадь треугольника
.
Решение.
Вписанный угол
опирается на диаметр окружности
Центр окружности лежит на середине основания
Диаметр окружности
Высота треугольника, проведенная к основанию
Площадь треугольника
Ответ:
Задача 4.
Катеты прямоугольного треугольника равны и , а гипотенуза равна .
Н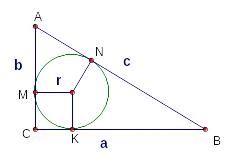
айдите
радиус вписанной окружности.
Решение.
Длины касательных к окружности равны
Радиус вписанной окружности
Ответ:
Задача 5.
Дан треугольник со сторонами 3, 4 и 5. Найдите радиус его описанной, вписанной и вневписанных окружностей.
Р
ешение.
Стороны треугольника
Площадь треугольника
Полупериметр треугольника
Радиус описанной окружности
Радиус вписанной окружности
Радиусы вневписанных окружностей
Ответ:
Задача 6.
Дан треугольник со сторонами 13, 13 и 10.
Найдите радиус его описанной, вписанной и вневписанных окружностей.
Р
ешение.
Высота, проведенная к основанию треугольника
Площадь треугольника
:
Радиус описанной окружности
Полупериметр
треугольника
:
Радиус вписанной
окружности
Радиусы вневписанных окружностей
Ответ:
Задача 7.
Дан треугольник со сторонами 13, 14 и 15.
Найдите радиус его описанной, вписанной и вневписанных окружностей.
Р
ешение.
Полупериметр
треугольника
Площадь треугольника
Радиус описанной окружности
Радиус вписанной
окружности
Радиусы вневписанных окружностей
Ответ:
Задача 8.
В равнобедренный треугольник с основанием, равным , вписана окружность, и к ней проведены три касательные, отсекающие от данного треугольника три треугольника, сумма периметров которых равна . Найдите боковую сторону данного треугольника.
Решение.
П
ериметры
треугольников
Сумма периметров всех треугольников
Длины касательных к окружности равны
Боковая сторона треугольника
Определим длину боковой стороны
.
Ответ:
Задача 9.
Проекция боковой стороны равнобедренной трапеции на большее основание равна , средняя линия трапеции равна , а острый угол при основании равен .
Найдите радиус окружности, описанной около трапеции.
Р
ешение.
Проекция боковой
стороны равнобедренной трапеции
В равнобедренном
треугольнике
- длина средней линии
Высота трапеции
Определим хорду по теореме Пифагора
Радиус окружности
определим из треугольника
.
Ответ:
Задача 10.
О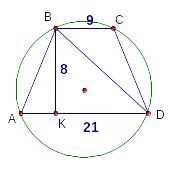
снования
равнобедренной трапеции равны 9 и 21, а
высота равна 8. Найдите радиус окружности,
описанной около трапеции.
Решение.
Длина отрезка
Радиус окружности
.
Ответ:
