Тема 10.
Пересекающиеся окружности.
Задача 1.
Прямая линия, проходящая через общую точку двух окружностей, пересекает вторично эти окружности в точках и соответственно.
Расстояние между проекциями центров окружностей на эту прямую линию равно 12.
Найдите , если известно, что точка лежит на отрезке .
Решение.
Предположим, что имеем внешнее касание двух окружностей разных радиусов.
Изобразим прямую линию , пересекающую окружности и проходящую через точку касания этих окружностей.
Р
адиус
окружности, перпендикулярный хорде
делит хорду на равные отрезки
- по условию задачи.
Аналогичный результат получим при внутреннем касании окружностей
Ответ: 24.
Задача 2.
Окружности с центрами
и
пересекаются в точках
и
.
Известно, что
.
Найдите радиусы окружностей.
Решение.
Окружности расположены по разные стороны от линии пересечения
Р
асстояние
между центрами
Радиусы окружностей
Треугольник
- равносторонний
Соотношения между радиусами окружностей
Проекции радиусов на ось центров
,
,
Окружности расположены по одну сторону от линии пересечения
,
,
.
Ответ:
или
Задача 3.
Отрезок, соединяющий центры двух пересекающихся окружностей, делится их общей хордой на отрезки, равные 5 и 2.
Найдите общую хорду, если известно, что радиус одной окружности вдвое больше радиуса другой окружности.
Р
ешение.
Рассмотрим прямоугольные
треугольники
и
Радиусы окружностей
Отрезки, на которые хорда делит отрезок линии центров
Применим теорему Пифагора
Ответ:
Задача 4.
Через вершину остроугольного треугольника проведена прямая линия, параллельная стороне , равной , и пересекающая окружности, построенные на сторонах и как на диаметрах, в точках и , отличных от точки .
Н
айдите
.
Решение.
Линия
Вписанные углы опираются на диаметр
Окружности пересекаются на стороне
Точка пересечения – точка .
Фигуры
и
- прямоугольники
Ответ:
Задача 5.
Две окружности пересекаются в точках и .
Через точку проведены диаметры и этих окружностей.
Найдите расстояние
между центрами окружностей, если
.
Решение.
Окружности пересекаются по одну сторону относительно хорды
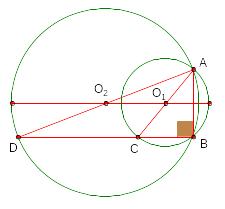
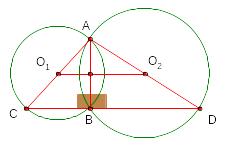
- средняя линия
треугольника
Окружности пересекаются по разную сторону относительно хорды
Ответ:
или
Задача 6.
В треугольнике на наибольшей стороне , равной , выбирается точка .
Найдите наименьшее
расстояние между центрами окружностей,
описанных около треугольников
и
.
Решение.
Задача заслуживает уважения.
Выберем на стороне произвольным образом точку .
Докажем, что расстояние между центрами будет наименьшим, если эта точка является пересечением высоты, опущенной из вершины на сторону .
Линия центров описанных около треугольников окружностей лежит на серединном перпендикуляре к стороне
Хорда является общей хордой при пересечении двух окружностей
Расстояние между
центрами
Отметим равные углы
и
Отрезки линии центров
и
Чем меньше радиусы окружностей, тем меньше расстояние между центрами.
Радиус будет наименьшим, если центры окружностей лежат на сторонах треугольника: и .
Тогда точка является пересечением высоты , проведенной к стороне .
Треугольники
и
- прямоугольные.
Центры окружностей лежат на серединах сторон.
Тогда - является средней линией треугольника с основанием
Изобразим полученную конфигурацию.
Ответ:
