
Тема 8: Касательная к окружности.
Задача 1.
В окружности проведен диаметр .
Прямая линия, проходящая через точку , пересекает в точке касательную к окружности, проведенной через точку .
Отрезок делится окружностью пополам.
Найти угол .
Решение.
Вписанный угол, опирающийся на диаметр - прямой.
![]()
Касательная перпендикулярна
к диаметру окружности
диаметру окружности
Отрезки
равны
![]() .
.
Медиана прямоугольного треугольника
![]()
Искомый
угол
![]()
Ответ:
Задача 2.
Две прямые линии касаются окружности с центром в точках и и пересекаются в точке .
Найдите
угол между этими прямыми линиями, если
![]()
Решение.
К асательная
перпендикулярна радиусу окружности
асательная
перпендикулярна радиусу окружности
![]()
Длины касательных равны.
Треугольник равнобедренный.
![]()
Углы при основании равны
![]()
Искомый
угол
![]()
Ответ:
![]()
Задача 3.
В большей из двух концентрических окружностей, имеющих общий центр, проведена хорда, равная 32 и касающаяся меньшей окружности.
Найдите радиус каждой из окружностей, если ширина образовавшегося кольца равна 8.
Р ешение.
ешение.
Радиус
![]() перпендикулярен хорде
перпендикулярен хорде
Ширина
кольца
![]()
Длина
хорды
![]() .
.
Треугольник равнобедренный.
Теорема
Пифагора для треугольника
![]()
![]()
![]()
Ответ: 20.
Задача 4.
Две прямые линии, проходящие через точку , лежащую вне окружности с центром , касаются окружности в точках и .
О трезок
трезок
![]() делится окружностью пополам.
делится окружностью пополам.
В каком отношении отрезок делится прямой линией ?
Решение.
По
условию
![]()
Касательная
![]()
Треугольник - прямоугольный.
-
медиана,
![]()
![]() -
радиус окружности.
-
радиус окружности.
![]() ,
,
![]()
Треугольник
![]() - равносторонний.
- равносторонний.
![]() ,
,
![]() .
.
![]()
![]()
Ответ:
![]()
Задача 5.
Из одной точки проведены к окружности две касательные.
Длина каждой касательной равна 12, а расстояние между точками касания равно 14,4.
Найдите радиус окружности.
Р ешение.
ешение.
![]()
По теореме Пифагора
![]()
Из подобия треугольников определим радиус окружности
![]()
Ответ: 9.
Задача 6.
П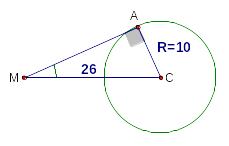 рямая
линия, проходящая через точку
,
удаленную от центра окружности радиуса
10 на расстояние, равное 26, касается
окружности в точке
.
рямая
линия, проходящая через точку
,
удаленную от центра окружности радиуса
10 на расстояние, равное 26, касается
окружности в точке
.
Найдите .
Решение.
Длина касательной
![]()
Ответ: 24.
Задача 7.
О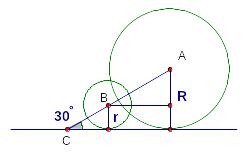 кружности
радиусов
кружности
радиусов
![]() и
и
![]() ,
,
![]() ,
касаются некоторой прямой линии. Линия
центров пересекает эту прямую линию
под углом
.
,
касаются некоторой прямой линии. Линия
центров пересекает эту прямую линию
под углом
.
Найдите расстояние между центрами окружностей.
Решение.
Окружности могут располагаться по одну сторону
от касательной или по разные стороны.
Имеем две конфигурации.
Конфигурация 1.
Расстояние между центрами
![]()

Конфигурация 2.
Расстояние между центрами
![]()
Ответ:
![]()
Задача 8.
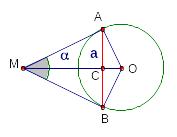
Из точки
проведены касательные
![]() и
и
![]() к окружности с центром
.
к окружности с центром
.
и - точки касания.
Найдите радиус
окружности, если
![]() и
и
![]() .
.
Решение.
![]()
![]()
Радиус окружности

Ответ:

Задача 9.
Окружность с центром касается двух параллельных прямых линий.
Проведена касательная к окружности, пересекающая эти прямые линии в точках и .
Н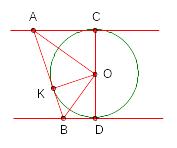 айдите
угол
.
айдите
угол
.
Длины касательных равны
![]()
![]()
и - биссектрисы углов.
При пересечении они образуют угол
Ответ:
Задача 10.
На окружности радиуса
выбраны три точки таким образом, что
окружность оказалась разделенной на
три дуги, градусные меры которых относятся
как
![]() .
.
В точках деления к окружности проведены касательные.
Найдите площадь треугольника, образованного этими касательными.
Решение.
Ц ентральный
угол
ентральный
угол
![]()
Центральный угол
![]()
Углы треугольника
![]()
![]()
Катеты треугольника
![]()
![]()
Площадь треугольника
![]()
Ответ:
![]()
Задача 11.
Расстояния от концов диаметра окружности до некоторой касательной равны и .
Найдите радиус окружности.
Решение.
Т рапеция
- прямоугольная.
рапеция
- прямоугольная.
Радиус окружности
![]()
![]() - средняя линия трапеции
- средняя линия трапеции
![]()
Ответ:
![]()
Задача 12.
В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки, равные 5 и 12. Найдите катеты треугольника.
Решение.
Д лины
касательных равны.
лины
касательных равны.
![]()
![]()
Теорема Пифагора
![]()
![]()
![]()
Ответ: 8 и 15.
Тема: Касающиеся окружности.
Подготовительные задачи.
Задача 1.
Три равных окружности радиуса касаются друг друга внешним образом. Найдите стороны и углы треугольника, вершинами которого служат точки касания.
Решение.
Р адиус
окружности
адиус
окружности
![]()
Расстояние между
центрами
![]()
Точки касания
окружностей
![]()
Длина сторон треугольника
:
![]()
Треугольник равносторонний
Углы треугольника равны .
Ответ:
![]()
Задача 2.
Две равных окружности касаются изнутри третьей окружностью и касаются между собой.
С оединив
три центра, получим треугольник с
периметром, равны 18.
оединив
три центра, получим треугольник с
периметром, равны 18.
Найдите радиус большей окружности.
Решение.
Радиусы меньших
окружностей
![]()
Радиус большей
окружности
![]()
Расстояние между
центрами
![]()
Периметр треугольника
![]() :
:
![]()
Радиус большей окружности
![]()
Ответ: 9.
Задача 3.
Три окружности радиусов 6, 7 и 8 попарно касаются друг друга внешним образом. Найдите площадь треугольника с вершинами в центрах этих окружностей.
Р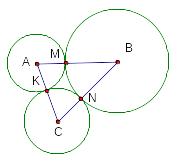 ешение.
ешение.
Радиусы окружностей
![]()
Длины сторон треугольника
![]()
Площадь треугольника определим по формуле Герона
Полупериметр
треугольника
![]()

Ответ: 84.
Задача 4.
Окружности радиусов 8 и 3 касаются внутренним образом. Из центра большей окружности проведена касательная к меньшей окружности. Найдите расстояние от точки касания до центра большей окружности.
Р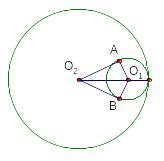 ешение.
ешение.
Требуется найти
отрезок
![]()
Расстояние между центрами
![]()
Радиус меньшей
окружности
![]()
Касательная
перпендикулярна радиусу
![]()
Треугольник
![]() прямоугольный.
прямоугольный.
По теореме Пифагора
![]()
Ответ: 4.
Задача 5.
Д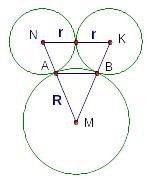 ве
окружности радиуса
касаются друг друга. Кроме того, каждая
из них касается извне третьей окружности
радиуса
в точках
и
соответственно.
ве
окружности радиуса
касаются друг друга. Кроме того, каждая
из них касается извне третьей окружности
радиуса
в точках
и
соответственно.
Найдите радиус
,
если
![]() .
.
Решение.
Треугольники
![]() и
и
![]() подобны
подобны
![]()
![]()
Ответ: 24.
Задача 6.
Две окружности радиуса касаются друг друга. Кроме того, каждая из них касается изнутри третьей окружности радиуса в точках и соответственно.
Найдите радиус
,
если
![]()
Р ешение.
ешение.
Треугольники и подобны

Ответ: 55
Задача 7.
Д ана
окружность радиуса
.
Четыре окружности равных радиусов
касаются данной внешним образом, и
каждая из этих четырех окружностей
касается двух других. Найдите радиусы
этих четырех окружностей.
ана
окружность радиуса
.
Четыре окружности равных радиусов
касаются данной внешним образом, и
каждая из этих четырех окружностей
касается двух других. Найдите радиусы
этих четырех окружностей.
Решение.
Радиус маленькой окружности
Радиусы окружностей при внешнем касании
Центры окружностей расположены в вершинах квадрата
Сторона квадрата
![]()
Диагональ квадрата
![]()
Определим радиусы окружностей по теореме Пифагора

![]()
Ответ:
![]()
Задача 8.
Три окружности разных радиусов попарно касаются друг друга внешним образом.
Отрезки, соединяющие их центры, образуют прямоугольный треугольник.
Н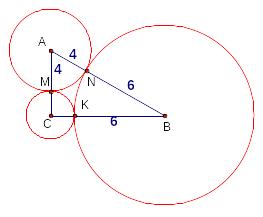 айдите
радиус меньшей окружности, если радиусы
большей и средней окружности равны 6 и
4.
айдите
радиус меньшей окружности, если радиусы
большей и средней окружности равны 6 и
4.
Решение.
Радиусы окружностей
![]()
![]()
Радиус меньшей
окружности
![]()
Теорема Пифагора

![]()
Ответ: 2
Задача 9.
На прямой линии, проходящей через центр окружности радиуса , взята точка на расстоянии от центра.
Найдите радиус второй
окружности, которая касается прямой
линии
![]() в точке
,
а также касается данной окружности.
в точке
,
а также касается данной окружности.
Решение.
Возможны два варианта: точка лежит внутри окружности, и точка лежит вне окружности.
В ариант
ариант
![]()
Треугольник
![]() прямоугольный
прямоугольный
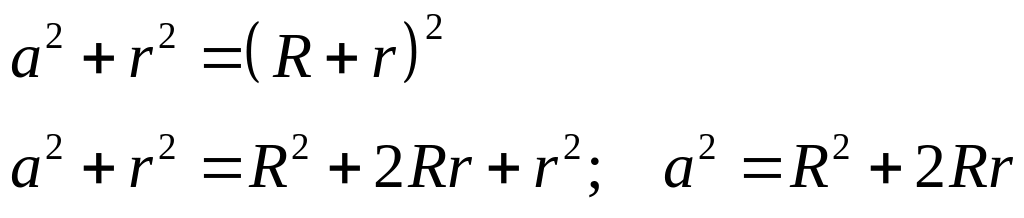
![]()

Вариант
![]()
Радиус касающейся окружности
Заданный радиус
окружности
![]()
Расстояние от центра
окружности до точки
![]()
Длина отрезка
![]()
Треугольник прямоугольный

Объединяя результаты
![]()
Ответ:
![]()
Задача 10.
Даны окружности радиусов 1 и 3 с общим центром .
Третья окружность касается их обеих.
Найдите угол между касательными к третьей окружности, проведенными из точки .
Решение.
Р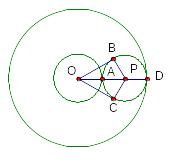 адиус
третьей окружности
адиус
третьей окружности
![]()
![]()
Отрезок
![]()
![]() - касательная,
- касательная,
![]()
![]()
Угол между касательными
![]()
Ответ:

Задача 11.
В угол, равный , вписаны две окружности,
касающиеся друг друга внешним образом.
Радиус меньшей окружности равен .
Найдите радиус большей окружности.
Решение.
Опустим из центра меньшей окружности
перпендикуляр к радиусу большей окружности
![]()
Отрезок
![]()
Расстояние между
центрами
![]()
![]() ,
,
![]()
![]()
Ответ:
![]()
Задача 12.
Две окружности касаются друг друга внутренним образом.
Известно, что два радиуса большей окружности, угол между которыми равен , касаются меньшей окружности.
Н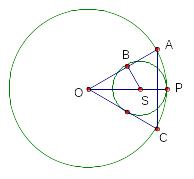 айдите
отношение радиусов окружностей.
айдите
отношение радиусов окружностей.
Решение.
Радиус большей окружности
Радиус меньшей окружности
![]()
![]()

Ответ:
![]()
Задача 13.
В равносторонний треугольник вписана окружность. Этой окружности и двух сторон треугольника касается меньшая окружность.
Найдите сторону треугольника, если радиус малой окружности равен .
Решение.
![]()
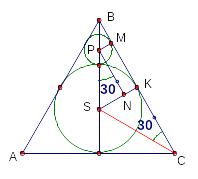
![]()
![]()
Сторона треугольника
![]()
Ответ:
![]()
Задача 14.
В круговой сектор с центральным углом
круговой сектор с центральным углом
![]() вписана окружность. Найдите ее радиус,
если радиус данной окружности равен
.
вписана окружность. Найдите ее радиус,
если радиус данной окружности равен
.
Решение.
![]()
![]()
![]()
![]()
Ответ:
![]()
Задача 15.
Две окружности касаются внешним образом в точке . Одна прямая линия касается этих окружностей в различных точках и , а вторая – соответственно в различных точках и . Общая касательная к окружностям, проходящая через точку , пересекается с этими прямыми в точках и .
Н айдите
,
если
айдите
,
если
![]()
Решение.
![]()
![]()
- средняя линия трапеции
![]()
Ответ:
