Литвинова С.А,
учитель математики
ГБОУ СОШ № 918
Решаем задачи по геометрии
Список предметов, которые наши сограждане считают обязательными для изучения в старшей школе, начинается с алгебры. Алгебру выбрали 70 % наших соотечественников. К сожалению, за геометрию проголосовали только 11 % россиян. Это повод задуматься и ученым-математикам, и методистам, и учителям – ведь кризис преподавания геометрии многим был ясен давно. Необходимо вернуть геометрии ее место в образовании и воспитании, которое ей принадлежало на протяжении всей истории человечества. В этом учебном году увеличена доля геометрических задач в содержании экзаменационных работ как в 9-х, так и в 11 классах. Вашему вниманию предлагается набор задач, которые можно использовать и на уроке, и во внеурочной работе для повышения образования молодого поколения.
Р
ешаем
задачи по геометрии.
Тема: Медиана прямоугольного треугольника.
Задача 1.
Гипотенуза прямоугольного треугольника равна 4.
Найдите радиус описанной окружности.
Решение.
Ответ:
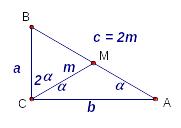
Задача 2.
Медиана,
проведенная к гипотенузе прямоугольного
треугольника, равна
и делит прямой угол в отношении
.
Найдите стороны треугольника.
Решение.
Необходимо видеть равнобедренный треугольник:
Ответ:
Задача 3.
Медиана прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два треугольника с периметрами 8 и 9. Найдите стороны треугольника.
Р
ешение.
Ответ:
Задача 4.
В
треугольнике
к стороне
проведена высота
и медиана
,
причем
.
Найдите косинус угла
,
если
.
Р
ешение.
,
Ответ:
Задача 5.
Окружность,
построенная на катете прямоугольного
треугольника как на диаметре, делит
гипотенузу в отношении
.
Найдите острые углы треугольника.
Решение.
В
писанный
угол опирается на диаметр.
Как важно знать вывод теоремы Пифагора.
Ответ:
,
Задача 6.
Точка
– середина гипотенузы
прямоугольного треугольника
.
Окружность, вписанная в треугольник
,
касается отрезка
в его середине. Найдите острые углы
треугольника
.
Решение.
О
кружность
вписана в треугольник
.
Окружность касается середины отрезка
.
.
– медиана, проведенная к стороне
.
Треугольник
– равнобедренный,
.
Длины касательных к окружности равны.
Треугольник – равносторонний.
Ответ:
Задача 7.
В
прямоугольном треугольнике
из вершины прямого угла
проведена биссектриса
и медиана
.
Найдите площадь треугольника
,
если
.
Р
ешение.
– медиана.
Свойство биссектрисы
Теорема
Пифагора
.
Умение работать с системой уравнений.
Определим катеты треугольника
,
,
Площадь треугольника
Ответ:
Задача 8.
Вне
прямоугольного треугольника
на его катетах
и
построены квадраты:
и
.
Продолжение медианы
треугольника
пересекает прямую линию
в точке
.
Н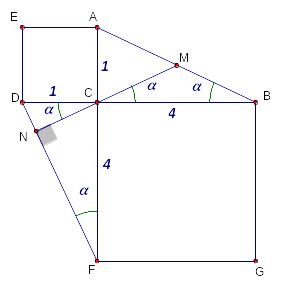
айдите
отрезок
,
если катеты равны 1 и 4.
Решение.
Хорошая задача – приятное построение. Главное интуиция.
Отметим
равные углы и обозначим как
.
Треугольник
– прямоугольный.
Следовательно,
Ответ:
Задача 9.
Высота
прямоугольного треугольника, проведенного
из вершины прямого угла, равна
и образует угол
с медианой, проведенной из той же вершины.
Найдите катеты треугольника.
Решение.
Отметим
равные углы. Задан угол между медианой
и высотой
.
– прямоугольный.
– внешний угол
–
равнобедренный.
Треугольники прямоугольные
Катеты
треугольника
,
Ответ:
Задача 10.
Медиана
прямоугольного треугольника, проведенная
к гипотенузе, разбивает его на два
треугольника с периметрами, равными
и
.
Найдите стороны треугольника.
Р
ешение.
Ответ:
Задача 11.
В
прямоугольном треугольнике
,
,
проведена высота
и медиана
.
Площади треугольников
и
равны соответственно 10 и 3. Найдите
.
Р
ешение.
,
,
Ответ:
Задача 12.
В
прямоугольном треугольнике
катеты
и
равны 4 и 3 соответственно. Точка
делит гипотенузу
пополам. Найдите расстояние между
центрами окружностей, вписанных в
треугольнике
и
.
Решение.
Треугольники
и
- равнобедренные. Центры окружностей
лежат на линиях
и
.
Площади треугольников
и
равны.
Площадь треугольника
:
Значение
площадей
Длина
гипотенузы
Полупериметры
треугольников
Радиусы
окружностей
Средняя
линия
и
:
Длины
катетов треугольника
:
,
Расстояние между центрами окружностей
Ответ:
Задача 13.
Катет
прямоугольного треугольника равен 2, а
противолежащий ему угол равен
.
Найдите расстояние между центрами
окружностей, вписанных в треугольники,
на которые данный треугольник делится
медианой, проведенной из вершины прямого
угла.
Решение.
С
тороны
треугольника
Площади треугольников
Полупериметры треугольников
Радиусы
окружностей
Длины
катетов треугольника
,
Расстояние между центрами окружностей
Ответ:
Задача 14.
В
четырехугольнике
диагонали
и
перпендикулярны и пересекаются в точке
.
Отрезок, соединяющий вершину
с серединой
отрезка
,
равен
,
.
Расстояние от точки
до отрезка
равно
.
Найдите
,
если известно, что вокруг четырехугольника
можно описать окружность.
Решение.
Плохо составлен текст.
Вначале лучше выделить окружность: вокруг четырехугольника описана окружность, или четырехугольник вписан в окружность.
Что это нам дает?
Сумма
противоположных углов равна
.
После проведения диагоналей можно отметить равные вписанные углы – углы, опирающиеся на одну и ту же дугу.
Диагонали четырехугольника перпендикулярны.
Отметим подобные треугольники.
Соотношение подобия
Точки
лежат на одной прямой линии.
Проведем
среднюю линию
,
Введем
параметр
Применим
теорему Пифагора для треугольника
Определим
переменную
Сторона
четырехугольника
Ответ:
Задача 15.
Средняя
линия трапеции равна 5, а отрезок,
соединяющий середины оснований, равен
3. Углы при большем основании трапеции
равны
и
.
Найдите площадь трапеции.
Решение.
За что зацепиться в этой задаче.
Хорошо бы знать длины сторон, а не длину средней линии. Тогда можно определить высоту трапеции. Попробуем это сделать.
Длины
сторон основания
и
.
Проведем боковые стороны трапеции до пересечения в точке . Медианы прямоугольных треугольников равны половине длины гипотенузы.
Решаем систему уравнений
Опять вернемся к вопросу:
как найти площадь трапеции.
Известна
формула
Получается, практически мы не сдвинулись. Не определена высота.
Как еще можно определить площадь трапеции?
Как разность двух площадей треугольников.
Здесь
и
– площади прямоугольных треугольников.
Площадь прямоугольного треугольника по заданной гипотенузе и острому углу
Площадь
трапеции
.
В качестве угла можно принять любой из острых углов
Кстати, можно было не решать приведенную систему
Можно поступить и по-другому.
Так
как треугольник
– равнобедренный, то угол
равен
Высота
трапеции
Площадь
трапеции
Ответ:
Задача 16.
Средняя
линия трапеции равна 4, углы при основании
равны
и
.
Найдите основания трапеции, если отрезок,
соединяющий середины оснований, равен
1.
Решение.
Так
как сумма углов при большем основании
равна
,
то отрезок, соединяющий середины
оснований равен разности половин
оснований.
Ответ:
Задача 17.
Диагонали
трапеции перпендикулярны. Одна из них
равна 6. Отрезок, соединяющий середины
оснований, равен
.
Найдите площадь трапеции.
Р
ешение.
Диагонали трапеции взаимно перпендикулярны
Длина
диагонали
Проведем линию до пересечения
с
основанием
.
Следовательно,
Проведем
Линия
является медианой треугольника
В
прямоугольном треугольнике
Определим по теореме Пифагора длину катета
Площадь трапеции равна площади треугольника
Ответ:
Задача 18. Нереальная задача. Много преобразований.
Прямая
линия, параллельная гипотенузе
прямоугольного треугольника
,
пересекает катет
в точке
,
а катет
– в точке
,
причем
.
На
гипотенузе взята такая точка
,
что
.
И
звестно
также, что
.
Найдите площадь треугольника .
Решение.
Проведем из точки линию,
параллельную катету
Линия
пересекает
линию
.
,
то отрезки
и
равны.
Фигура
- ромб, со стороной равной 1.
Точка
– середина гипотенузы треугольника
- медиана треугольника
Треугольник
- равнобедренный.
.
Внутренние
накрест лежащие углы равны:
-
биссектриса угла
Определим длину биссектрисы по теореме синусов
Определим длину отрезка по теореме косинусов
,
Длина
отрезка
Определим
Площадь
треугольника
:
Площадь треугольника :
Ответ:
Задача 19.
Гипотенуза
прямоугольного треугольника
является хордой окружности радиуса 10.
Вершина
лежит на диаметре окружности, который
параллелен гипотенузе. Угол
равен
.
Найдите площадь треугольника
.
Р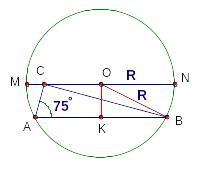
ешение.
Из центра окружности опустим
перпендикуляр
к хорде
Обозначим гипотенузу треугольника
:
Катеты треугольника
Высота треугольника, опущенная на гипотенузу
Рассмотрим
треугольник
По теореме Пифагора
Площадь треугольника :
Ответ: 40
Тема: Удвоение медианы.
Задача 2.1.
Медиана
треугольника
равна
и образует со сторонами
и
углы
и
соответственно. Найдите эти стороны.
Решение.
Достроим треугольник до параллелограмма на сторонах и .
Для
этого на продолжении луча
отложим отрезок
.
Диагонали и в точке пересечения делятся пополам,
фигура
– параллелограмм.
Диагональ
параллелограмма
.
Внутренние
накрест лежащие углы равны
Используем теорему синусов.
О
тметим,
что
.
-
противоположные стороны параллелограмма
Ответ:
,
Задача 2.2.
В треугольнике известно, что - медиана,
.
.
Найдите
.
Решение.
Построим
параллелограмм
.
Треугольник
– прямоугольный
Ответ:
Задача 2.3.
Найдите площадь треугольника, если две стороны соответственно равны 27 и 29, а медиана, проведенная к третьей стороне, равна 26.
Р
ешение.
Достроим треугольник до параллелограмма .
Стороны
треугольника
Медиана
треугольника
.
Длина диагонали параллелограмма
Площади
треугольников
и
.
Площадь треугольника
равна
площади треугольника
Площадь треугольника определим по формуле Герона
Полупериметр
треугольника
Стороны
треугольника
Ответ:
Задача 2.4.
Стороны треугольника равны 11, 13 и 12. Найдите медиану, проведенную к большей стороне.
Решение.
Достроим треугольник до параллелограмма
Требуемую медиану превратим в диагональ параллелограмма
Воспользуемся соотношением в параллелограмме
В данной формуле и – стороны параллелограмма,
и
- диагонали параллелограмма
Длина
медианы
определим
из приведенной формулы
Ответ:
Задача 2.5.
В треугольнике две стороны равны 11 и 23, а медиана, проведенная к третьей стороне, равна 10. Найдите третью сторону.
Р
ешение.
Стороны
треугольника
.
Медиана
проведена к неизвестной стороне
.
Достроим треугольник до параллелограмма.
Определим сторону треугольника из равенства
Ответ:
.
Задача 2.6.
В равнобедренном треугольнике с боковой стороной, равной 4, проведена медиана к боковой стороне. Найдите основание треугольника, если медиана равна 3.
Р
ешение.
Построим параллелограмм
- медиана треугольника.
,
Длина основания
Ответ:
Задача 2.7.
Основание
равнобедренного треугольника равно
,
а медиана, проведенная к боковой стороне,
равна 5. Найдите боковые стороны.
Решение
Построим параллелограмм
О
пределим
длину боковой стороны
Ответ:
Задача 2.8.
В
треугольнике
известны стороны
и медиана
.
Найдите
.
Решение.
Для нахождения искомого угла необходимо знать стороны треугольника .
Построим параллелограмм
Определим
Можно воспользоваться теоремой косинусов.
Воспользуемся обратной теоремой Пифагора и покажем, что угол
Длина
отрезка
Определим острый угол прямоугольного треугольника
Ответ:
Задача 2.9.
В треугольнике отрезок – медиана,
.
Найдите
.
Решение
О
пределим
неизвестную сторону треугольника
Используем свойство параллелограмма
Воспользуемся теоремой косинусов
Значение
угла
Ответ:
Тема: Параллелограмм. Средняя линия.
Задача 3.1.
Р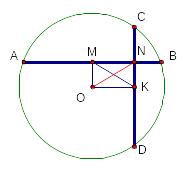
асстояние
между серединами взаимно перпендикулярных
хорд
и
некоторой окружности равно 10. Найдите
диаметр окружности.
Решение.
Фигура
– прямоугольник.
Диагонали
прямоугольника равны.
.
– радиус
окружности.
Диаметр
окружности
Ответ: 20.
Задача 3.2.
Д
иагональ
параллелограмма делит его угол на части:
и
.
Найдите отношение сторон параллелограмма.
Решение.
Теорема
синусов
Ответ:
Задача 3.3.
Вершины
и
квадрата
лежат на гипотенузе
прямоугольного треугольника
.
Точка
лежит между точками
и
.
Вершины
и
лежат на катетах
и
соответственно.
Известно,
что
.
Найдите площадь квадрата.
Р
ешение.
Сторона квадрата
Треугольники
и
подобны
Площадь
квадрата
Ответ:
Задача 3.4.
Сторона параллелограмма вдвое больше стороны .
Биссектрисы
углов
и
пересекают прямую линию
в точках
и
,
причем
.
Найдите стороны параллелограмма.
Решение.
Обозначим стороны параллелограмма
Биссектриса угла проходит через середину стороны
Отрезки
Аналогично, точка лежит
на середине стороны
Треугольники
и
равны.
Треугольники
и
Отрезки
Ответ: 4 и 8.
Задача 3.5.
Найдите расстояние от центра ромба до его стороны, если острый угол равен , а сторона равна 4.
Р
ешение.
Расстояние от центра ромба до стороны
определим из равенства площадей.
Искомое
расстояние
Площадь
ромба
Площадь
ромба
Ответ: 1.
Задача 3.6.
В четырехугольнике известны углы:
.
Кроме
того,
.
Найдите расстояние между центрами
окружностей, одна из которых проходит
через точки
,
а другая – через точки
.
Решение.
Вписанный угол величиной опирается на диаметр.
Для прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
Т
очки
и
– центры окружностей.
Определим
катет треугольника
-
средняя линия треугольника
Ответ:
Задача 3.7.
На
сторонах
и
прямоугольника
взяты точки
и
так, что
– ромб. Диагональ
образует со стороной
угол
.
Найдите сторону ромба, если наибольшая сторона прямоугольника равна 3.
Решение.
Определим точки и построением.
П
роведем
диагональ
и определим его середину – точку
.
Восстановим
перпендикуляр
.
Диагональ прямоугольника
является диагональю ромба.
Второй диагональю ромба является
отрезок
Определим большую диагональ ромба
Определим
сторону ромба
Ответ:
Тема: Трапеция.
Задача 4.1.
Найдите площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные 17 и 25.
Решение.
Определим проекции боковых сторон на основание
Определим высоту трапеции
Площадь
трапеции
Ответ: 450.
Задача 4.2.
Найдите площадь трапеции с основаниями 11 и 4 диагоналями 9 и 12.
Решение.
Проведем
линию
до пересечения с продолжением стороны
Фигура
- параллелограмм
Площадь
трапеции
равна площади треугольника
Т
реугольник
- прямоугольный.
Обратная теорема Пифагора.
Площадь треугольника
:
Площадь
трапеции
Ответ: 54.
Задача 4.3.
В равнобедренной трапеции основания равны 40 и 24, а ее диагонали взаимно перпендикулярны. Найдите площадь трапеции.
Р
ешение.
- ось симметрии.
,
и длины оснований.
Площадь
трапеции
Ответ: 1024.
Задача 4.4.
Д
иагонали
равнобедренной трапеции перпендикулярны.
Найдите площадь трапеции, если ее средняя
линия равна 5.
Решение.
Площадь
трапеции
Диагонали перпендикулярны.
Боковые стороны равны.
Высота
трапеции
Длина
средней линии
Площадь
трапеции
Ответ: 25.
Задача 4.5.
Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25.
Найдите высоту трапеции. Найдите высоту трапеции.
Решение.
Длины хорд основания трапеции параллельны.
Д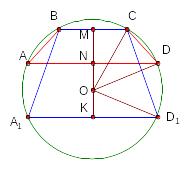
лины
оснований различаются.
Трапеция равнобедренная,
так как вписана в окружность.
Возможные варианты
вписанной трапеции.
Трапеция
или
Проводим ось симметрии трапеции.
Высоты
трапеции:
или
-
центр окружности.
-
радиус окружности.
Определим отрезки, перпендикулярные основаниям трапеции.
Высоты трапеции
О
твет:
9 или 39.
Задача 4.6.
Диагональ равнобедренной трапеции равна 10
и образует угол с основанием трапеции.
Найдите среднюю линию трапеции.
Решение.
Для
равнобедренной трапеции
- длина средней линии
Ответ: 5
Задача 4.7.
Окружность с центром вписана в трапецию с боковой стороной .
Найдите
угол
.
Решение.
О
трезки
и
- биссектрисы углов
и
.
Ответ:
Задача 4.8.
Меньшая боковая сторона прямоугольной трапеции равна 3, а большая образует угол с одним из оснований. Найдите это основание, если на нем лежит точка пересечения биссектрис углов при другом основании.
Решение.
и
- биссектрисы углов.
Д
лина
большей боковой стороны
Треугольник
равнобедренный
Длина большего основания
Ответ: 9
Задача 4.9.
Основания трапеции равны 1 и 6, а диагонали равны 3 и 5.
Под каким углом видны основания из точки пересечения диагоналей?
Решение.
П
роводим
Теорема косинусов для треугольника
,
,
Ответ:
Задача 4.10.
Основания
трапеции равны
и
.
.
Найдите длину отрезка, соединяющего
середины диагоналей трапеции.
Решение.
-
средняя линия трапеции.
Ответ:
Задача 4.11.
Основания равнобедренной трапеции равны и . .
Острый угол трапеции равен . Найдите площадь трапеции.
Р
ешение.
Высота
трапеции
Средняя линия трапеции
Площадь трапеции
Ответ:
Как находить высоты и биссектрисы треугольника.
Подготовительные задачи.
Задача 1.
Катет и гипотенуза прямоугольного треугольника равны 12 см и 20 см соответственно. Найдите высоту, проведенную из вершины прямого угла.
Решение.
Длина
катета
Высота, проведенная из вершины прямого угла
Ответ:
Задача 2.
Найти высоту прямоугольного треугольника, опущенную на гипотенузу, если известно, что основание этой высоты делит гипотенузу на отрезки, равные 1 и 4.
Решение.
Высота
прямоугольного треугольника
Ответ: 2.
Задача 3.
Высота равнобедренного треугольника, опущенная на боковую сторону, разбивает ее на отрезки, равные 2 и 1, считая от вершины треугольника. Найдите эту высоту.
Решение.
Введем
параметры задачи
Длина
боковой стороны
Высота перпендикулярна боковой стороне.
Высоту определим по теореме Пифагора
Ответ:
Задача 4.
Стороны треугольника равны 10,17 и 21. Найдите высоту треугольника, проведенную из вершины наибольшего угла.
Решение.
Периметр
треугольника
Полупериметр
Площадь треугольника определим по формуле Герона
Высота проведена к большей стороне треугольника.
Длина
высоты
Ответ: 4.
Задача 5.
В
треугольнике
известно, что
.
Найдите биссектрису .
Решение.
Площадь
треугольника
Биссектриса
делит угол пополам. Длина биссектрисы
Площадь треугольника, как сумма площадей двух треугольников
Из равенства площадей определим длину биссектрисы
Ответ:
Задача 6.
Катеты прямоугольного треугольника равны и
Найдите биссектрису треугольника, проведенную из вершины прямого угла.
Решение.
Площадь
треугольника
.
Биссектриса делит угол пополам. Угол между катетом и биссектрисой равен . Длина биссектрисы Площадь треугольника, как сумма площадей двух треугольников
Из равенства площадей определим длину биссектрисы
Ответ:
Задача 7.
В
треугольнике
известно, что
.
Найдите биссектрису .
Решение.
Площадь
треугольника
Биссектриса делит угол пополам. Длина биссектрисы .
Площадь треугольника
Из равенства площадей определим длину биссектрисы
Ответ:
Задача 8.
Найдите высоту трапеции, боковые стороны которой равны 6 и 8,
а основания равны 4 и 14.
Р
ешение.
Из точки проведем прямую линию .
.
Обратная теорема Пифагора
Треугольник прямоугольный.
Проведем высоту трапеции .
Из
равенства площадей
Ответ:
